Aký je faktor proporcionality? (Vyriešené cvičenia)

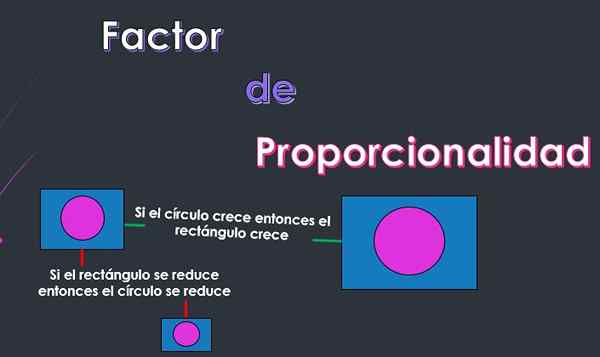
On faktor proporcionality o Konštanta proporcionality je číslo, ktoré naznačuje, do akej miery sa zmení druhý objekt vo vzťahu k zmene, ktorú utrpel prvý objekt.

Napríklad, ak sa hovorí, že dĺžka schodiska je 2 metre a že tieň, ktorý tento projekt je 1 meter (faktor proporcionality je 1/2), potom ak sa schodisko zníži na dĺžku 1 meter, Tieň úmerne zníži svoju dĺžku, a preto bude dĺžka tieňa 1/2 metra.

Ak sa naopak, schodisko sa zvýši na 2.3 metre, potom bude dĺžka tieňa 2.3*1/2 = 1.15 metrov.

Proporcionalita je konštantný vzťah, ktorý je možné vytvoriť medzi dvoma alebo viacerými objektmi tak, že ak jeden z objektov utrpí akúkoľvek zmenu, potom ďalšie objekty prechádzajú zmenou.

Napríklad, ak sa hovorí, že dva objekty sú úmerné z hľadiska jeho dĺžky, bude mať, ak sa objekt zvýši alebo zníži jeho dĺžku, potom sa druhý objekt tiež zvýši alebo zníži jeho dĺžku úmerne.

Koncept faktora proporcionality

Faktor proporcionality je, ako je uvedené v vyššie uvedenom príklade, konštanta, ktorou sa musí vynásobiť, aby sa získala druhá veľkosť.

V predchádzajúcom prípade bol faktor proporcionality 1/2, pretože schodisko „X“ meralo 2 metre a tieň „y“ meral 1 meter (polovica). Preto musíte y = (1/2)*x.

Takže keď sa zmení „x“, potom sa zmení aj „y“. Ak je to „y“, ktorý sa mení, potom sa zmení aj „x“, ale faktor proporcionality je iný, v takom prípade by to bolo 2.

Proporcionálne cvičenia

- Prvé cvičenie

Juan chce pripraviť koláč pre 6 ľudí. Recept, ktorý Juan hovorí, že koláč má 250 gramov múky, 100 gramov masla, 80 gramov cukru, 4 vajcia a 200 mililitrov mlieka.

Predtým, ako začne pripravovať koláč, si Juan uvedomil, že recept, ktorý má, je na tortu pre 4 ľudí. Aké by mali byť veľkosti, ktoré musí Juan použiť?

Riešenie

Tu je proporcionalita nasledovná:

4 ľudia - 250 g múka - 100 g masla - 80 g cukru - 4 vajcia - 200 ml mlieka

6 osôb -?

Faktor proporcionality v tomto prípade je 6/4 = 3/2, čo by sa dalo chápať, akoby sa prvýkrát vydelil 4, aby sa získali prísady na osobu, a potom vynásobte 6, aby sa koláč pre 6 ľudí urobil.

Vynásobením všetkých množstiev o 3/2 sú prísady pre 6 ľudí:

6 osôb - 375 g múka - 150 g masla - 120 g cukru - 6 vajíčok - 300 ml mlieka.

- Druhé cvičenie

Dve vozidlá sú identické, s výnimkou ich pneumatík. Polomer pneumatík vozidla sa rovná 60 cm a polomer pneumatík druhého vozidla sa rovná 90 cm.

Ak po prehliadke musíte dať množstvo kôl, ktoré dali pneumatiky s menším polomerom, bolo 300 kôl. Koľko zákrut dalo najväčšie rádiové pneumatiky?

Riešenie

V tomto cvičení sa proporcionálna konštanta rovná 60/90 = 2/3. Takže ak radiu menšie pneumatiky dali 300 kôl, pneumatiky s najvyšším rádiom dali 2/3*300 = 200 kôl.

- Tretie cvičenie

Je známe, že 3 pracovníci maľovali za 5 hodín stenu 15 -kvadrát. Koľko môžu maľovať 7 pracovníkov za 8 hodín?

Riešenie

Údaje uvedené v tomto cvičení sú:

3 pracovníci - 5 hodín - 15 m² steny

A čoho sa pýta, je:

7 pracovníkov - 8 hodín -- ? M².

Môžete sa opýtať, koľko 3 pracovníkov by maľovali za 8 hodín? Aby som to vedel, riadok údajov dodávaný v proportnom faktore 8/5 sa vynásobí. To ukazuje v dôsledku toho:

3 pracovníci - 8 hodín - 15*(8/5) = 24 m² steny.

Teraz chcete vedieť, čo sa stane, ak sa počet pracovníkov zvýši na 7. Vedieť, aký účinok vytvára množstvo steny maľovanej faktorom 7/3. To dáva konečné riešenie:

7 pracovníkov - 8 hodín - 24*(7/3) = 56 m² steny.

Odkazy

1. Cofré, a., & Tapia, l. (Devätnásť deväťdesiatpäť). Ako rozvíjať matematické logické zdôvodnenie. Redakcia univerzity.
2. Advanced Telerasporte Physics. (2014). Edu nasz.
3. Giancoli, D. (2006). Zväzok fyziky I. Pearson Vzdelanie.
4. Hernández, J. d. (s.F.). Notebook matematiky. Prah.
5. Jiménez, J., Rofríguez, m., & Estrada, r. (2005). Matematika 1 september. Prah.
6. Neuhauser, C. (2004). Matematika pre vedu. Pearson Vzdelanie.
7. Peña, m. D., & Muntaner,. R. (1989). Fyzikálna chémia. Pearson Vzdelanie.
8. Segovia, b. R. (2012). Matematické aktivity a hry s Miguelom a Lucíou. Baldomero Rubio Segovia.
9. Tocci, r. J., & Widmer, n. Siež. (2003). Digitálne systémy: princípy a aplikácie. Pearson Vzdelanie.