Vektorová algebra

Čo je vektorová algebra?

On Vektorová algebra Je to odvetvie matematiky zodpovednej za štúdium systémov lineárnych rovníc, vektorov, matíc, vektorových priestorov a ich lineárnych transformácií. Súvisí s oblastiami, ako je inžinierstvo, rozlíšenie diferenciálnych rovníc, funkčná analýza, výskum operácií, výpočtová grafika.

Ďalšou z oblastí, ktoré prijala lineárna algebra, je fyzika, pretože vďaka tomu bolo možné vyvinúť štúdium fyzikálnych javov a opisovať ich pomocou vektorov. To umožnilo lepšie porozumieť vesmíru.

Základy

Vektorová algebra pochádza zo štúdia kvarterniónov (rozšírenie skutočných čísel) 1, I, J a K, ako aj karteziánska geometria podporovaná Gibbs a Heaviside, ktorí si uvedomili, že vektori budú slúžiť ako nástroj pre reprezentáciu pre reprezentáciu pre reprezentáciu pre reprezentáciu pre reprezentáciu pre reprezentáciu niekoľko fyzikálnych javov.

Vektorová algebra je študovaná prostredníctvom troch základov:

Geometricky

Vektory sú reprezentované čiarami, ktoré majú orientáciu, a operácie, ako je súčet, odčítanie a násobenie skutočnými číslami, sú definované geometrickými metódami.

Analyticky

Opis vektorov a ich operácie sa vykonáva s číslami, nazývanými komponentmi. Tento typ opisu je výsledkom geometrického znázornenia, pretože sa používa súradnicový systém.

Axiomaticky

Vytvára sa opis vektorov bez ohľadu na súradnicový systém alebo akýkoľvek typ geometrického znázornenia.

Štúdium obrázkov vo vesmíre sa vykonáva prostredníctvom jeho reprezentácie v referenčnom systéme, ktorý môže byť v jednej alebo viacerých rozmeroch. Medzi hlavné systémy patria:

• Jednorozmerný systém, Že je to čiara, v ktorej bod (alebo) predstavuje pôvod a ďalší bod (P) určuje mierku (dĺžku) a smer tohto:

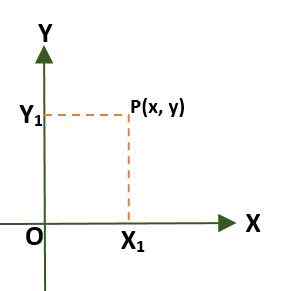
• Obdĺžnikový súradnicový systém (dva rozmery), ktoré sa skladajú z dvoch kolmých čiar nazývaných os x a y, ktoré prechádzajú bodovým (alebo) pôvodom; Týmto spôsobom je plán rozdelený do štyroch regiónov nazývaných kvadranty. V tomto prípade je bod (p) v rovine daný vzdialenosťami, ktoré existujú medzi osami a p.

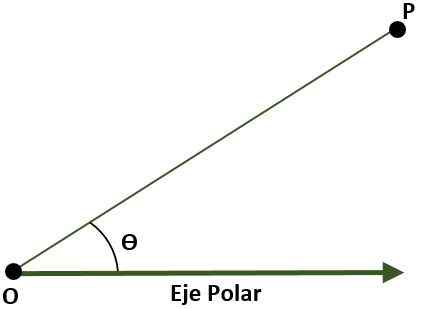
• Polárny systém (dva rozmery). V tomto prípade sa systém skladá z bodu O (pôvod), ktorý sa nazýva pól a semi -réver s pôvodom v alebo sa nazýva polárna osi alebo sa nazýva polárna osi. V tomto prípade je bod P roviny s odkazom na pól a polárnu os daný uhlom (ɵ), ktorý je tvorený vzdialenosťou medzi pôvodom a bodom P.

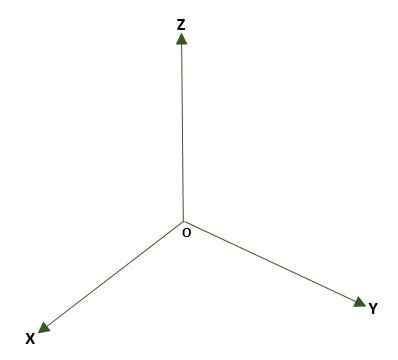
• Obdĺžnikový trojrozmerný systém, tvorené tromi kolmými čiarami (x, y, z), ktoré majú ako svoj bod alebo vo vesmíre. Vytvárajú sa tri súradnicové lietadlá: XY, XZ a YZ; Priestor sa rozdelí do ôsmich regiónov nazývaných oktanty. Referencia bodu P priestoru je daná vzdialenosťami, ktoré existujú medzi rovinami a P.

Veľkoleposť

Veľkosť je fyzické množstvo, ktoré je možné počítať alebo merať pomocou numerickej hodnoty, ako v prípade niektorých fyzikálnych javov; Často je však potrebné opísať tieto javy s inými faktormi, ktoré nie sú číselné. Preto sú veľkosti klasifikované do dvoch typov:

Skalárnosť

Sú to tie sumy, ktoré sú definované a reprezentované numerickým spôsobom; to znamená, modul spolu s jednotkou merania. Napríklad:

A) Čas: 5 sekúnd.

b) Hmotnosť: 10 kg.

c) Zväzok: 40 ml.

D) Teplota: 40 ° C.

Vektor

Sú to sumy, ktoré sú definované a reprezentované modulom spolu s jednotkou, ako aj zmyslom a smerom. Napríklad:

Môže vám slúžiť: Symbolizácia výrazov

A) Rýchlosť: (5ȋ - 3ĵ) m/s.

b) Zrýchlenie: 13 m /s²; S 45 ° E.

c) Sila: 280 N, 120 °.

d) Hmotnosť: -40 ĵ kg -f.

Vektorové veľkosti sú graficky reprezentované vektormi.

Čo sú vektory?

Vektory sú grafické znázornenie vektorovej veľkosti; to znamená, že sú to segmenty riadkov, v ktorých je jeho konečný koniec špičkou šípky.

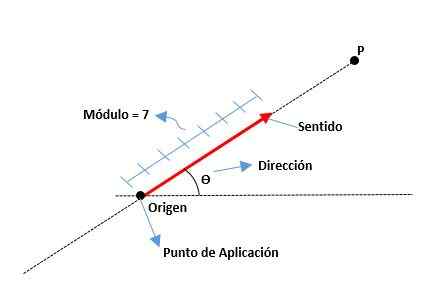
Tieto sú určené jeho modulom alebo dĺžkou segmentu, ich zmyslom, ktorý je označený špičkou jej šípky a smerom podľa čiary, ku ktorej patrí. Pôvod vektora je tiež známy ako bod aplikácie.

Prvky vektora sú nasledujúce:

Modul

Je to vzdialenosť od pôvodu do konca vektora, reprezentovaná skutočným číslom spolu s jednotkou. Napríklad:

| Om = | A | = A = 6 cm

Osloviť

Je to miera uhla, ktorá existuje medzi osou X (z pozitívneho) a vektorom, ako aj kardinálne body (sever, juh, východ a západ).

Zmysel

Je daný špičkou šípky umiestnenej na konci vektora, čo naznačuje, kde je nasmerovaný.

Klasifikácia vektorov

Všeobecne sú vektory klasifikované ako:

Pevný vektor

Je to ten, ktorého aplikačný bod (pôvod) je pevný; to znamená, že zostáva spojený s priestorom vesmíru, takže sa v tomto nemôže pohnúť.

Vektor

Môže sa pohybovať voľne vo vesmíre, pretože jeho pôvod sa presúva do akéhokoľvek bodu bez zmeny modulu, významu alebo smeru.

Posuvný vektor

Je to ten, ktorý dokáže preniesť svoj pôvod pozdĺž svojej činnosti bez zmeny modulu, významu alebo smeru.

Vektorové vlastnosti

Medzi hlavné vlastnosti vektorov patrí:

Vybavovacie vektory

Sú to tie voľné vektory, ktoré majú rovnaký modul, smer (alebo sú rovnobežné) a zmysel ako posuvný vektor alebo pevný vektor.

Rovnocenné vektory

Vyskytuje sa, keď majú dva vektory rovnakú adresu (alebo sú rovnobežné), rovnaký zmysel a napriek tomu, že majú rôzne moduly a aplikačné body, spôsobujú rovnaké účinky.

Vektorová rovnosť

Majú rovnaký modul, smer a zmysel, aj keď sú ich východiskové body odlišné, čo umožňuje paralelnému vektorovi presunúť sa k sebe bez toho, aby ho ovplyvnil.

Oproti vektorom

Sú to tí, ktorí majú rovnaký modul a smer, ale ich význam je opačný.

Jednotný vektor

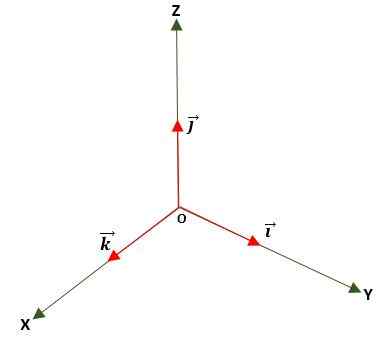
Je to jeden, v ktorom sa modul rovná jednotke (1). Toto sa získa vydelením vektora jeho modulom a používa sa na určenie smeru a smeru vektora, buď v rovine alebo vo vesmíre pomocou štandardizovaných základných alebo jednotkových vektorov, ktoré sú:

Nulová vektor

Je to ten, ktorého modul sa rovná 0; to znamená, jeho bod pôvodu a extrémne sa zhodujú v rovnakom bode.

Vektorové komponenty

Komponenty vektora sú hodnoty vektorových projekcií na osiach referenčného systému; V závislosti od rozkladu vektora, ktorý môže byť v osi dvoch alebo troch rozmerov, sa získajú dve alebo tri zložky.

Komponenty vektora sú reálne čísla, ktoré môžu byť kladné, záporné alebo dokonca nulové (0).

Týmto spôsobom, ak máte ā vektor, ktorý pochádza z obdĺžnikového súradnicového systému v rovine XY (dvojrozmerná), projekcia na osi x je āx a projekcia na osi y a je āy. Vektor bude teda vyjadrený ako súčet svojich vektorov zložiek.

Príklady

Prvý príklad

Máte ā vektor, ktorý začína od pôvodu a súradnice jeho koncov sú uvedené. Teda vektor ā = (ā_X; Do_a) = (4; 5) cm.

Môže vám slúžiť: 120 deliteľov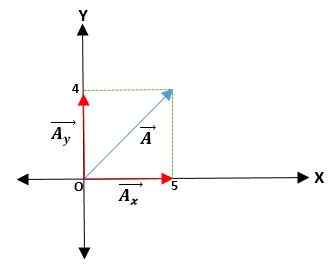

Ak vektor ā pôsobí na pôvod trojrozmerného trojuholníkového súradnice (vo vesmíre) x, y, z, do iného bodu (P), projekcie na ich osiach budú āx, āy a āz; Vektor bude teda vyjadrený ako súčet svojich troch zložkových vektorov.

Druhý príklad

Máte ā vektor, ktorý začína od pôvodu a súradnice jeho koncov sú uvedené. Teda vektor ā = (a_X; Do_a Do_z) = (4; 6; -3) cm.

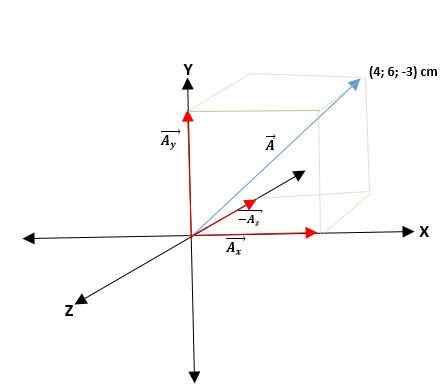
Vektory, ktoré majú svoje obdĺžnikové súradnice, sa dajú vyjadriť podľa svojich základných vektorov. Z tohto dôvodu sa musí vynásobiť iba každá súradnica vektorom jednotky, takže pre rovinu a priestor budú nasledujúce:

Pre lietadlo: ā = a_Xi +a_aJ.

Pre priestor: ā = a_Xi +a_aJ+a_zklimatizovať.

Operácie s vektormi

Existuje veľa veľkostí, ktoré majú okrem iného modul, význam a smer, ako napríklad zrýchlenie, rýchlosť, vytesnenie, sila,.

Uplatňujú sa v rôznych oblastiach vedy a na ich uplatňovanie je v niektorých prípadoch potrebné vykonávať operácie, ako je súčet, odčítanie, násobenie a delenie vektorov a skalárov.

Pridanie a odčítanie vektorov

Súčet a odčítanie vektorov sa považujú za jedinú algebraickú operáciu, pretože odčítanie sa dá písať ako suma; Napríklad odčítanie vektorov ā a ē možno vyjadriť ako:

Ā - ē = ā + (-ē)

Existujú rôzne metódy na vykonanie súčtu a odčítania vektorov: môžu to byť grafika alebo analytika.

Grafické metódy

Používa sa, keď má vektor modul, zmysel a smer. Na tento účel sú čiary, ktoré tvoria obrázok, ktorý následne pomáha určiť výsledné. Medzi najznámejšie patrí:

Metóda rovnobežníka

Aby sa dosiahol súčet alebo odčítanie dvoch vektorov, na súradnicovej osi sa vyberie spoločný bod, ktorý bude predstavovať bod pôvodu vektorov -udržiavať ich modul, smer a smer a smer.

Potom sa k vektorom nakreslia paralelné čiary, aby sa vytvoril rovnobežník. Výsledný vektor je diagonál, ktorý odchádza od bodu pôvodu oboch vektorov do vrcholu rovnobežníka:

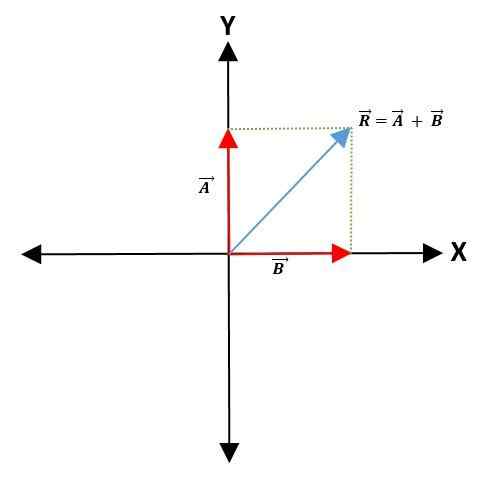
Trojuholník

V tejto metóde sú vektory umiestnené pod druhou a udržiavajú svoje moduly, zmysly a adresy. Výsledný vektor bude spojením pôvodu prvého vektora s koncom druhého vektora:

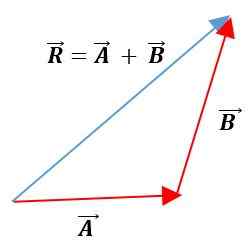
Analytické metódy

Dva alebo viac vektorov je možné pridať alebo odpočítať geometrickou alebo vektorovou metódou:

Geometrická metóda

Keď dva vektory tvoria trojuholník alebo rovnobežník, M [Odulo a smer výsledného vektora sa dá určiť pomocou zákonov prsníka a kosínu. Výsledný vektorový modul, ktorý uplatňuje zákon kozine a metódou trojuholníka, je teda daný:

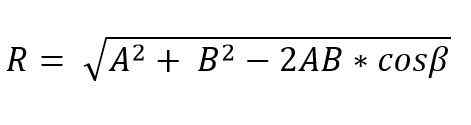
V tomto vzorci je p.

Na druhej strane metódou rovnobežníka je výsledný vektorový modul:

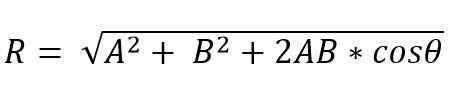
Výsledná vektorová adresa je daná uhlom (a), ktorý tvorí výslednú hodnotu s jedným z vektorov.

Podľa zákona o prsníku je možné súčet alebo odčítanie vektorov vykonať aj metódou trojuholníka alebo rovnobežníka, pretože vie, že v každom trojuholníku sú strany úmerné prsníkom pekných uhlov:

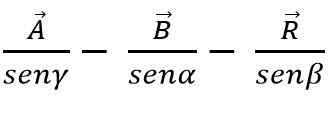
Vektorová metóda

To sa dá urobiť dvoma spôsobmi: v závislosti od jeho obdĺžnikových súradníc alebo jeho základných vektorov.

Vektory, ktoré sa budú pridávať alebo odpočítať smerom k pôvodu súradníc, sa môžu vykonať a potom sa všetky projekcie rozdelia na svoje obdĺžnikové komponenty v každej zo osí pre rovinu (x, y) alebo priestor (x, x, a z); Nakoniec sa jeho komponenty pridávajú algebraicky. Takže pre lietadlo je to:

Môže vám slúžiť: Primo čísla: Charakteristiky, príklady, cvičenia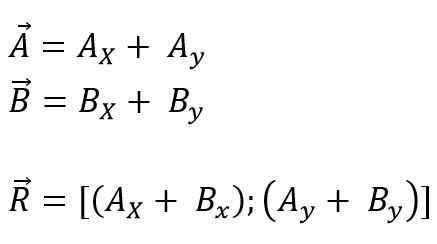

Výsledný vektorový modul je:

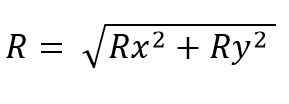
Zatiaľ čo pre priestor je:

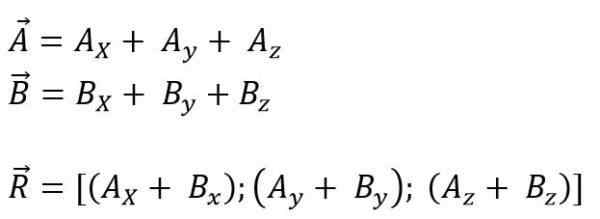
Výsledný vektorový modul je:

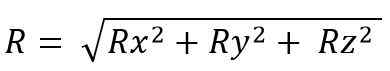
Ak sa vykonávajú vektorové sumy, použije sa niekoľko vlastností, ktoré sú:

• Asociatívna vlastnosť: Výsledok sa nemení najskôr pridaním dvoch vektorov a potom pridaním tretieho vektora.
• Komutatívne vlastníctvo: Poradie vektorov nemení výsledné výsledky.
• Distribučná vlastnosť vektorov: Ak sa skalár vynásobí súčtom dvoch vektorov, rovná sa mu násobenie skalárneho pre každý vektor.
• Distribučná vlastnosť skalárna: Ak sa vektor vynásobí súčtom dvoch skalár.

Násobenie vektora

Násobenie alebo produkt vektorov by sa mohol vykonávať ako súčet alebo odčítanie, ale pri tom stráca fyzický význam a takmer nikdy nie je v aplikáciách. Preto je všeobecne najpoužívanejším typom výrobkov skalárny a vektorový produkt.

Skalárny produkt

Je tiež známy ako bod dvoch vektorov. Keď sa dva -vektorové moduly vynásobia menším uhlom kosínus, ktorý je medzi nimi vytvorený, získa sa skalár. Na vyjadrenie skalárneho produktu medzi dvoma vektormi je umiestnený bod medzi nimi, ktorý možno definovať ako:

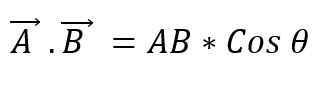
Hodnota uhla, ktorý existuje medzi týmito dvoma vektormi, bude závisieť od toho, či sú rovnobežné alebo kolmé; Preto musíte:

• Ak sú vektory rovnobežné a majú rovnaký zmysel, coseno 0 ° = 1.
• Ak sú vektory rovnobežné a majú opačné zmysly, coseno 180 ° = -1.
• Ak sú vektory kolmé, coseno 90 ° = 0.

Tento uhol je možné vypočítať aj s vedomím, že:

Skalárny produkt má nasledujúce vlastnosti:

• Kombutatívny majetok: Rád vektorov nemení skalár.
• Distribučná vlastnosť: Ak sa skalár vynásobí súčtom dvoch vektorov, rovná sa mu násobenie skalárnych pre každý vektor.

Vektorový produkt

Násobenie vektora alebo krížový produkt dvoch vektorov A a B bude mať za následok nový vektor C a vyjadruje sa pomocou kríža medzi vektormi:

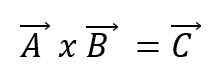
Nový vektor bude mať svoje vlastné vlastnosti. Tým smerom:

• Ten osloviť: Tento nový vektor bude kolmý na rovinu, ktorá je určená pôvodnými vektormi.
• On zmysel: Toto je určené pravou pravou rukou, kde sa vektor A otočí na B, ktorý ukazuje smer rotácie prstami a palcom smerom vektora je označený.
• On modul: Je určená násobením modulov vektorov AXB, linkou menšieho uhla, ktorý existuje medzi týmito vektormi. Je vyjadrené:

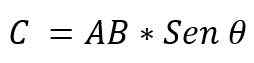
Hodnota uhla, ktorý existuje medzi týmito dvoma vektormi, bude závisieť od toho, či sú rovnobežné alebo kolmo. Takže je možné potvrdiť:

• Ak sú vektory rovnobežné a majú rovnaký význam, sínus 0 ° = 0.
• Ak sú vektory rovnobežné a majú opačné zmysly, sínus 180 ° = 0.
• Ak sú vektory kolmé, sínus 90 ° = 1.

Ak je vektorový produkt vyjadrený podľa svojich základných vektorov, musí:

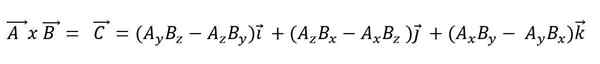
Skalárny produkt má nasledujúce vlastnosti:

• Nie je to komutatívne: poradie vektorov mení skalár.
• Distribučná vlastnosť: Ak sa skalár vynásobí súčtom dvoch vektorov, rovná sa mu násobenie skalárnych pre každý vektor.