Hooke Law Formulas, príklady, žiadosti, cvičenia

Ten Hookeov zákon poukazuje na to, že deformácia, ktorú zažíva elastický objekt, je priamo úmerná aplikovanej sile na ňu. Konštanta proporcionality závisí od povahy objektu, jeho geometrie a materiálu, s ktorým sa vyrába.

Všetky materiály majú elastické vlastnosti vo väčšej alebo menšej miere, takže dodržiavajú Hookeov zákon vždy, keď sa vrátia do svojich pôvodných rozmerov, keď sila prestane. Elastické pramene a ďasná sú dobrými príkladmi predmetov, ktoré sú v súlade so zákonom Hooke, ale aj oceľové kabíly, ktoré sú súčasťou mosta.

postava 1. Hookeov zákon na jar

Ako príklad, pružina alebo dok, aby sa udržala natiahnutá alebo stlačená, je potrebné použiť silu, ktorej veľkosť je f. Podľa Hookeovho zákona bude jar zažiť deformáciu X:

F ∝ x

Konštanta proporcionality, ktorá sa nazýva jar stuhnutosť, Je označovaný ako K, preto:

F = k⋅x

V jednotkách medzinárodného systému sa sila prichádza v Newtone (N) a deformácii v metroch (M). Preto má pružinová konštanta N/M jednotky. Konštanta pružiny predstavuje silu, ktorá sa musí aplikovať na deformovanie v dĺžke 1 m.

Obrázok 2. Keď je pružina natiahnutá, sila vyvíjaná na objekt je naopak. To isté sa stane, ak sa pružina zmenšuje, v tomto prípade riadi objekt v opačnom zmysle. Zdroj: Wikimedia Commons.

Ak po natiahnutí alebo komprimovaní pružiny je uvoľnená, bude sa pohybovať v opačnom smere k použitej sile. To znamená, že ak ho natiahneme, je komprimovaná a naopak. Preto sila f_R taký Jarné cvičenia je:

F_R = -K⋅x

Negatívne znamenie naznačuje, čo sa hovorí: že sila je proti posunu, takže táto sila je známa ako Restoratívna sila.

[TOC]

Vzorec a rovnice

Vzťah medzi silou a vysídlením na jar objavil Robert Hooke (1635-1703), pozoruhodný anglický fyzik a známy svojou súperením s Izákom Newtonom. Hooke bol všestranný vedec, ktorý úspešne fušoval v rôznych oblastiach vedy: mechanika, biológia, astronómia a architektúra.

Obrázok 3. Anglický fyzik Robert Hooke, ktorý nepozná portréty času. Toto je rekonštrukcia umelca Rita Gerera v roku 2004 prostredníctvom opisov, ktoré zanechali tí, ktorí sa stretli s vedcom. Zdroj: Wikimedia Commons. Rita Greer / Fal.

Hooke si uvedomil, že ak sila aplikovaná na mólo nie je príliš veľká, prístavisko je úmerne deformované k sile a akonáhle povedala, že sila zmizne, pružina má svoju prirodzenú dĺžku opäť svoju prirodzenú dĺžku.

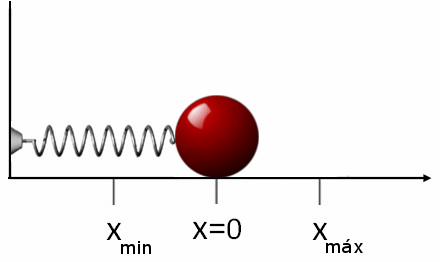
Môže vám slúžiť: Zemská magnetosféra: Charakteristiky, štruktúra, plyny

Týmto spôsobom má Hookeov zákon graficky tvar priamky, ktorej sklon je pružinová konštanta. Nasledujúci obrázok zobrazuje silu vyvíjanú na pružine, ktorá ju natiahne - alebo ju komprimuje - v závislosti od polohy X. Všimnite si, že sila nezávisí od prirodzenej dĺžky pružiny, ale od jej posunu.

Obrázok 4. Veľkosť f potrebnej sily na natiahnutie alebo stlačenie pružiny, v závislosti od deformácie X. Zdroj: Giancoli, D. Fyzika s aplikáciami.

Priemerná sila je uvedená v grafe f s panelou a je rovnocenná s ½ kx_F, kde x_F je konečná poloha jari.

Sila vyvíjaná na pružinu a sila, ktorú uplatňuje na objekt zviazaný s ním, sú premenlivé sily. Čím viac sa chcete natiahnuť alebo komprimovať na jar, tým väčšia sila musíte použiť, aby ste ju mohli dosiahnuť.

Práca vykonaná na natiahnutie alebo komprimovanie pružiny

Ak sa aplikuje sila, ktorá deformuje pružinu, je hotové dielo, ktoré sa ukladá na jar a ktoré sa dá použiť neskôr.

Mechanická práca je definovaná ako oblasť pod grafom sily F v závislosti od polohy x. Na výpočet práce w, ktorú robí premenná sila f (x) pri pohybe objektu z polohy x₁ do polohy x₂ Definovaný integrál sa musí vypočítať:

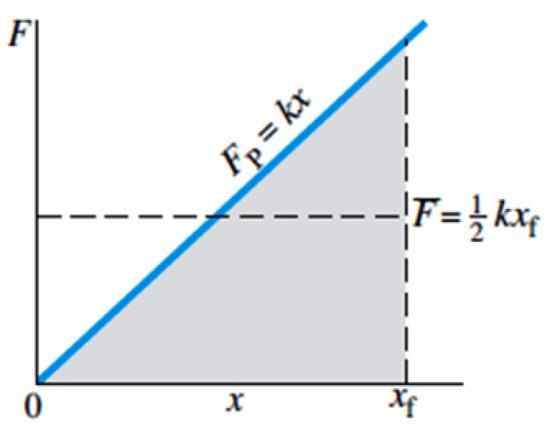
V prípade práce potrebnej na to, aby sa pružina priniesla z jej rovnovážnej polohy do polohy x_F Je to veľmi jednoduché, pretože oblasť, ktorá sa má vypočítať, je oblasť šedého zatieneného trojuholníka na obrázku 4, ktorého vzorec je známy:

Oblasť trojuholníka = ½ základňa. výška

Preto je potrebná práca:

W = ½ x_F . (KX_F) = ½ K (x_F)²

A ak chcete vypočítať potrebné práce, aby ste priniesli na pružinu z polohy X do polohy X_F, Bolo by to ekvivalentné výpočtu plochy poškriabaného lichobežníka na obrázku 5:

W = ½ K (x_F)² - ½ k x²

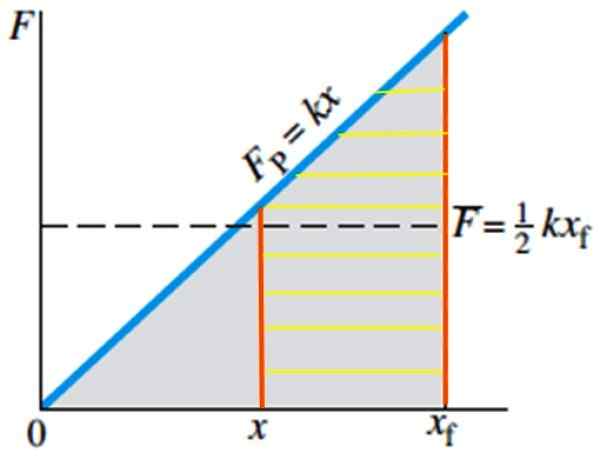Obrázok 5. Práca vykonaná na roztiahnutie pružiny od polohy X do polohy XF, ktorá je rovnajúca sa oblasti Rayada. Zdroj: Giancoli, D. Fyzika s aplikáciami.

Príklady prameňov

Podľa aplikácie, na ktorú sú určené, môžu byť pružiny valcové, kužeľové špirálové, s kruhovým prierezom (najbežnejším), štvorcovej alebo obdĺžnikovej časti.

Môže vám slúžiť: elektrické vodiče

Všeobecne používaná klasifikácia je podľa typu úsilia, ku ktorému budú vystavené: existujú torzie, flexia, kompresia a predlžovacie pramene. Posledne menované sa používajú vo veľkej miere a pracujú tiež pre napätie a kompresiu.

Kompresná pružina

Príkladom kompresnej pružiny je to, čo sa používa v hračke zvanej Pogo ani Saltoín Palo. Tieto pružiny ukladajú pomerne potenciálnu energiu, keď sú stlačené a uvoľnené postupne pri návrate do rovnovážnej polohy. Týmto spôsobom nie sú doskoky príliš náhle.

Obrázok 6. Pogo alebo Saltoínova palica je založená na kompresnej pružine. Zdroj: Wikimedia Commons.

Predlžovacie a torzné pramene

Pružina pre pružiny sú typom predlžovacích pružín a vyrábajú sa s dobre vlečnými zákrutami, s dvoma háčikmi na koncoch. Sú schopní udržať si dostatok potenciálnej energie, ktorú neskôr uvoľnia, keď niekto stúpa a začne skočiť na plátno, čo má tiež vlastnú elastickú reakciu, rovnako ako všetky materiály.

Torsion Springs sú veľmi bežné, pretože slúžia na výrobu svoriek na odevy. Namiesto háčikov na koncoch sa ohýbajú pod uhlom, aby odolali silám, ktoré majú tendenciu cvičiť torziu.

Obrázok 7. Springs sú súčasťou nespočetných mechanizmov, ako sú tieto odevné pinzety. Zdroj: pxfuel.

Materiály pre výrobné pramene

Najvhodnejšie materiály na výrobu prameňov sú tie, ktoré majú a Konečný odpor (konečný odpor), to znamená, že podporujú veľké úsilie pred zlomením. Je tiež vhodné, aby materiál mal vysoký bod tečenia, takže nestratí svoje elastické vlastnosti s malým úsilím.

Priemyselné používanie sa vyrábajú s zliatinami, ktoré zahŕňajú oceľ s vysokým obsahom uhlíka, medi, niklu a bronzového obsahu.

Hookeove zákonné žiadosti

Keďže pramene majú cnosť ukladania potenciálnej energie, keď sa natiahnú alebo komprimujú, sú schopní pracovať tým, že sa pohybujú s vecami, ako sú mechanizmy.

Týmto spôsobom majú pružiny veľa aplikácií, od malých a denných predmetov, cez autá až po stroje všetkých druhov. Springy slúžia:

-Šokové vibrácie.

-Výroba zatiahnuteľných mechanizmov: pero, zavesenie pinzety, háčiky na vlasy.

-Robiť pružinu alebo dynamometre

A sú tiež súčasťou mechanizmu:

Môže vám slúžiť: zatvorený elektrický obvod

-Hodinky.

-Trampolíny.

-Zámky.

-Hračky.

-Zbrane.

-Izle, napríklad galvanometer, používaný na meranie prúdov, napätia a odporov.

Vyriešené cvičenia

- Cvičenie 1

Použije sa sila veľkosti 5.0 n na pružine, čím sa dá dĺžka 3 úsek.5 cm od jeho prirodzenej dĺžky.

a) Koľko sa natiahne, keď je aplikovaná sila 7 n?

b) Nájdite prácu vykonanú aplikovanou silou, aby sa natiahla na jar 3.5 cm od jeho prirodzenej dĺžky.

Roztok

S vedomím, že pružina je natiahnutá 3.5 cm uplatňovaním 5.0 n Môžeme vypočítať vašu konštantu:

k = f / x = 5.0 n / 3.5 cm = 1.43 n / cm.

Keď sa použije sila 7 N, získa sa nasledujúci úsek:

x = f / k = 7.0 n / 1.43 N/m = 4.9 cm

Riešenie B

Potrebná práca na deformovanie pružiny je daná:

W = ½ kx² = 0.5 x 1.43 N / cm x (3.5 cm)² = 8.76 n . cm = 8.76 n . 1 x10 ^-2 m = 0.0876 J.

- Cvičenie 2

Spring zúfalého cesta a 10 cm dlhé visí od podpory. Ak je hmotnosť 2 kg obesená, pružina sa roztiahne, až kým nedosiahne 15 cm. Vypočítať:

a) pružina konštanta

b) Veľkosť pružiny, keď je zavesená hmotnosť 3 kg.

Roztok

Jarný úsek je x = 15 - 10 cm = 5 cm

Keďže systém je v statickej rovnováhe, sila vyvíjaná pružinou pri natiahnutí sa nasmeruje vertikálne smerom nahor, aby sa kompenzovala hmotnosť, ktorá je nasmerovaná nadol, potom:

F_R = W → kx = mg

K = 2 x 9.8 N / 5 x10 ^-2 M = 392 n/m

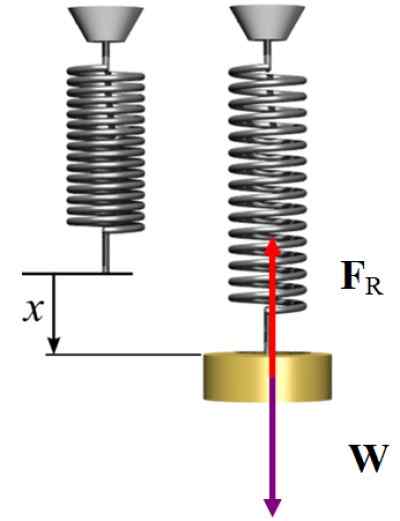Diagram voľného tela pre cvičenie vyriešené 2. Zdroj: Wikimedia Commons/F. Zapata.

Riešenie B

Keď je zavesená hmotnosť 3 kg, nová sila je W = 3 x 9.8 n = 29.4 n

V tomto prípade je úsek:

x = mg /k = 29. 4 N / 392 N / M = 0.075 m = 7.5 cm

Odkazy

1. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill.
2. Kreatívne mechanizmy blog. Štyri rôzne typy prameňov. Získané z: kreativicechanizmov.com.
3. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 2. Dynamika. Editoval Douglas Figueroa (USB).
4. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6. Edimatizovať. Sála.
5. Rytier, r.  2017. Fyzika pre vedcov a inžinierstvo: Strategický prístup.  Pearson.