Fickov zákon

Čo je to Fickov zákon?

Ten Fickov zákon Je to matematická rovnica, ktorá sa týka hmotnostného prietoku šíreného v médiu s koncentráciami alebo gradientom tlaku. Bol formulovaný v roku 1855 nemeckým fyziológom a doktorom Adolfom Fickom, ktorý sa inšpiroval Fourierove zákony (tepelné vedenie) a OHM (elektrické vedenie), modelovali proces difúzie kyslíka do alveol pľúc pľúc.

Fickov zákon predstavuje osobitnosť, že je použiteľný iba na chemické alebo biochemické difúzne javy, ale aj na fenomény akéhokoľvek druhu prírody. Preto slúži na modelovanie šírenia atómov medzi tuhými látkami, ktoré je veľmi užitočné vo fyzike materiálov a inžinierstva.

Zastúpenie difúzneho procesu prostredníctvom semiperpermosabilnej membrány. Zdroj: Gabriel Bolívar.

Centrálna základňa je však rovnaká pre takmer všetky difúzne javy, ktoré sú ilustrované vyššie. Fialové častice, atómy alebo molekuly, sa šíria cez semipermakciu hrubú membránu L a priečnu plochu do. Vľavo máme väčšiu koncentráciu C₁ častíc, ktoré vpravo, c₂.

Fickov zákon stanovuje nasledujúce: Hmotný tok, ktorý sa šíri povrchom, je úmerný koncentračnému gradientu (C₂-C₁/L) a konštanta D nazývaná koeficient difúzie alebo difúzivity.

Tento zákon má dve formy: jedna založená na priestore (x) a druhá v závislosti od priestoru a času (x, t). Prvý sa vzťahuje pre systémy v stacionárnych podmienkach, zatiaľ čo druhý pre skutočné, nestacionárne systémy.

Fickov prvý zákon

Komponenty a rovnica

Hrubá L semiperpermosabilnej membrány predstavuje vzdialenosť (x), že častice musia cestovať, aby dosiahli druhú stranu. Ako je možné vidieť na obrázku, fialové častice, čím viac sa pohybujú od ľavého priestoru, kde C₁ Je to skvelé, jej koncentrácia klesá na hodnotu C₂. To znamená, že koncentrácia sa mení pozdĺž hrúbky membrány, závisí od x.

Táto variácia koncentrácie v závislosti od vzdialenosti je známa ako koncentračný gradient: (C₂-C₁)/L o (c₂-C₁)/X. Všimnite si, že jeho hodnota je záporná (-1), pretože C₂ > C₁.

Na druhej strane máme tiež rýchlosť, s akou sa častice šíria cez membránu alebo dotknutý priestor. Táto rýchlosť závisí od veľkosti a hmotnosti častíc, ako aj od povahy prostredia a teploty. Difúzny koeficient D predstavuje túto rýchlosť a môže byť konštantný alebo nie počas difúzie.

Môže vám slúžiť: laboratórny filter): Charakteristiky, funkcie, typy

A nakoniec, máme hmotnostný tok „j“, ktorý prechádza priečnou plochou membrány alebo kanála, kde sa častice šíria. Zoskupenie týchto podmienok sa zrodí rovnica prvého zákona Ficku:

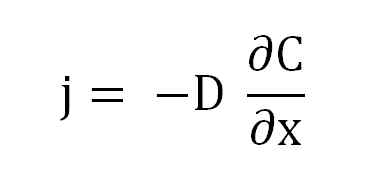Rovnica prvého zákona Ficku. Zdroj: Gabriel Bolívar.

Kde j je úmerný k d a a (∂c/∂x), koncentračný gradient.

Interpretácia a jednotky

Negatívny symbol v rovnici slúži na neutralizáciu negatívneho znaku gradientu koncentrácií. Inak by J mala zápornú hodnotu, ktorá je nezasiahnutá. Podobne je hodnota D pozitívna, takže vynásobením záporným znakom, ktorý mu predchádza, poskytuje zápornú hodnotu.

Fickov prvý zákon označuje nasledujúce: čím väčší je gradient koncentrácie (∂c/∂x), tým väčší je hmotnostný tok j. To znamená rozdiel medzi C₂ a c₁ Zväčší sa, a preto sa cez membránu šíri viac častíc.

Na druhej strane J závisí aj od D, ktorý zase závisí od parametrov, ako je teplota, viskozita, molekulová hmotnosť a priečna oblasť na:

D ∝ (a/l) (s/√m_W)

Kde S je rozpustnosť častíc, ktorá sa šíri v prostredí a m_W Jeho molekulová hmotnosť.

Pokiaľ ide o jednotky komponentov alebo podmienok rovnice, ktorú máme:

-C (kg · m^-3 alebo mol · m^-3)

-D (m^-2· S^-1)

-J (kg · m^-2· S^-1 alebo mol · m^-2· S^-1)

Čistý kvadratický posun

Počas šírenia sa častice navzájom zrážajú a po krátkodobom časovom intervaloch skončia cestovaním obrovskými vzdialenosťami δx. Avšak v závislosti od významu týchto posunov môže mať δx záporné alebo pozitívne hodnoty (podľa bodu pôvodu). Preto priemer hodnôt Ax pre všetky molekuly má tendenciu 0.

Na druhej strane, hodnoty Ax sú veľmi malé v porovnaní so vzdialenosťami, ktoré prevádzkujú častice. Keď sa zrazia, strácajú mobilitu smerom smerom, čo majú obmedzené čisté vysídlenie; Napríklad 2 cm postup v jednom smere po cestovaní stovky metrov v zrážkach a doskokoch.

Einstein v roku 1905 našiel matematický výraz pre priemerný posúvanie posunu (preto sa líši od 0):

<(Δx)²> = 2dt

Definujúci

(Δx)_Rms ≡ <(Δx)²>^1/2 = (2dt)^1/2

(Δx)_Rms Je to priemerný čistý kvadratický posun príslušných častíc. (Δx)_Rms Hovorí nám, koľko častíc sa pohybuje v priemere (v pozitívnom alebo negatívnom smere) podľa času. Niektoré častice sa budú pohybovať ďalej alebo najbližšie vzdialenosti ako (δx)_Rms, spôsobujúce gaussovské rozdelenie.

Môže vám slúžiť: oxid vápenatý (CAO)

Druhý zákon

Rovnica

Fickov prvý zákon popisuje difúziu v stacionárnych podmienkach, to znamená, že hmotnostný tok j sa v priebehu času nemení. V skutočných systémoch však máme nestacionárne podmienky, kde sa tok hmotnosti nielen líši vo vesmíre, ale aj v priebehu času. Preto sa zaujíma o určenie (∂c/∂t).

Nižšie máme dve rovnice, ktoré predstavujú Fickov druhý zákon:

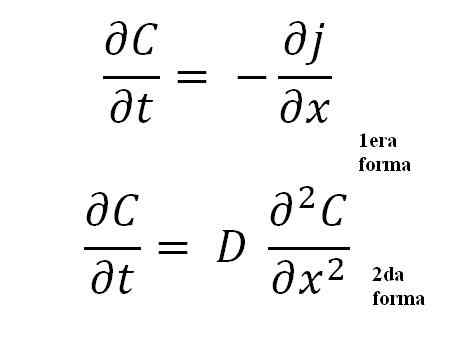Rovnice druhého zákona Ficku. Zdroj: Gabriel Bolívar.

Druhá forma je najdôležitejšia zo všetkých, pretože predstavuje všeobecnú matematickú rovnicu pre akýkoľvek proces šírenia; Buď tepelné, elektrické, atómové atď.

Odpočet

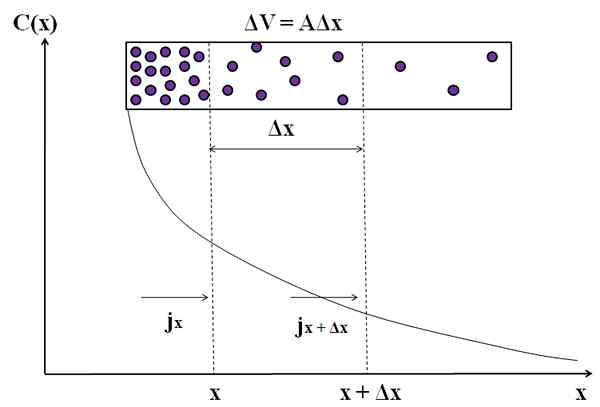Grafické znázornenie toho, ako nie je tok hmotnosti konštantný pri šírení týchto molekúl. Zdroj: Gabriel Bolívar.

Zoberme si znova fialové častice v obdĺžnikovej komore. Medzi vzdialenosťami x a x+δx máme tok j_X (prichádzajúci) a j_x+δx (vychádzajúce). Objem fotoaparátu medzi týmito vzdialenosťami je definovaný podľa:

ΔV = A5

Všimnite si, že graf C (x) vs x nepochádza po priamke, takže máme rôzne hodnoty j (j_X ≠ j_x+δx). Musíme určiť ΔC/δt.

Hmota m_X Bude to rovnaké:

m_X = J_X AAt

Dimenzionálna analýza pomáha pochopiť, prečo:

kg = (kg · m^-2· S^-1) (M²)

Rovnakým spôsobom vypočítame m_x+δx:

m_{x+ δx} = J_x+δx AAt

Byť hmotnosť, ktorá sa hromadí v tejto oblasti rovnajúcou sa ΔM:

ΔM = m_X - m_{x+ δx}

= (j_X - J_{x+ δx}) AAt

= -(j_{x+ δx} - J_X) AAt

= -AJAATT

A s vedomím, že ΔC = ΔM/ΔV

ΔC = -AJAAH/ AV

= -AJAAT /AAX

= -AjAt/δx

Vyčistíme δc/Δt

Δc/Δt = -Aj/δx

Táto expresia naznačuje, že variácia koncentrácie v priebehu času sa rovná variácii prietoku j vzhľadom na jeho posunutie. Použitie limitov pre AT a AX, ktoré majú tendenciu na 0, dostaneme rovnaký výraz ako čiastočný derivát:

∂c/∂t = -(∂j/∂x) (1. formulár)

Nakoniec sa druhý formulár získa nahradením J Fickov prvým zákonom:

∂c/∂t = -∂/∂x (-d∂c/∂x)

= D (∂²C/∂x²) (2. formulár)

Vyriešené cvičenia

V nasledujúcich cvičeniach sa budú brať do úvahy veľmi jednoduché systémy, ktorých neznámych sa dajú vyriešiť pomocou prvého zákona Ficku.

Cvičenie 1

Vyhlásenie

V potrubí s rozlohou 15 metrov dlhá a 21 centimetrov, ktorá je tiež nasýtená dusíkom, sa kyslíkový prúd šíri z jedného konca na druhý pri teplote 0 ° C. S vedomím, že tlak na ľavej strane (P₁) je 20 kg/m³, A že tlak na pravej strane (P₂) je 10 kg, určte:

Môže vám slúžiť: Hydronio ión

a) Tok hmotnosti, ktorý sa šíri

b) Koľko kilogramov alebo₂ Roztiahnu sa cez potrubie za 17 minút?

c) koncentračný gradient alebo tlaky

d) tlak O₂ vo vzdialenosti 7 metrov od vchodu do plynovodu

e) Koľko bude 80 kg O₂ Pri šírení tejto potrubia?

Zvážte to D_O2-n2 sa rovná 1.8 · 10^-5 m²· S^-1.

Rozhodnutie

Z prvého zákona Fick musíme vyriešiť pododdiel A):

J = -D (P₂-P₁)/L

= -(1.8 · 10^-5 m²· S^-1) (10-20) (kg/m³)/(15 m)

= 1.2 · 10^-5 kg · m^-2· S^-1

Do b) potrebujeme oblasť potrubia:

A = π (0.21 m)²

= 0.14 m²

A vynásobíme j o a a čas t, aby sme určili hmotnosť alebo₂ Neusradený:

m_O2 = (1.2 · 10^-5 kg · m^-2· S^-1) (17 s) (0.14 m²)

= 3.57 · 10^-5 kg

Teraz pre pododdiel C) máme, že gradient sa rovná:

Gradient = (P₂-P₁)/L

= (10-20) (kg/m³)/15 m

= -2/3 (kg/m³) · M^-1

Berieme však pozitívnu hodnotu, ktorá má fyzický zmysel:

2/3 (kg/m³) · M^-1

Táto hodnota nám potom bude slúžiť na vyriešenie pododdielu d) ak je gradient dobre interpretovaný: každý meter tlak alebo₂ 2/3 kg/m padne³. Šírením 7 metrov budeme mať:

2/3 (kg/m³) · M^-1 (7 m) = 14/3 alebo 4.7 kg/m³

To znamená, že tlak v tejto vzdialenosti bude:

(20-4.7) (kg/m³) = 15.3 kg/m³

A nakoniec, pododdiel E) je podobný ako b), iba to, že teraz vyčistíme čas a nie hmotnosť:

m_O2 = Jat

t = m_O2/Ja

= (80 kg)/(1.2 · 10^-5 kg · m^-2· S^-1) (0.14 m²)

= 47619.04 s alebo 0.55 dní

Cvičenie 2

Vyhlásenie

Stanovte (δx)_Rms Pre sacharózu vo vode pri t = 1 minútach, 1 h a 1 deň. Koeficient šírenia sacharózy vo vode je 0.52 · 10^-5cm²· S^-1.

Rozhodnutie

Uplatňujeme rovnicu:

(Δx)_Rms ≡ <(Δx)²>^1/2 = (2dt)^1/2

Hodnotíme (ΔX)_Rms S časmi vyjadrenými v sekundách. Pre t = 1 minútu alebo 60 s:

(Δx)_Rms = ((2 (0.52 · 10^-5cm²· S^-1) (60 s)))^1/2

= 0.025 cm

Pre t = 1 h alebo 3600 s:

(Δx)_Rms = ((2 (0.52 · 10^-5cm²· S^-1) (3600 s))^1/2

= 0.19 cm

A nakoniec pre t = 1 deň alebo 86400 s:

(Δx)_Rms = ((2 (0.52 · 10^-5cm²· S^-1) (86400 s))^1/2

= 0.95 cm

Všimnite si, že s časom prebieha molekuly sacharózy, ani sa nedokázali pohybovať 1 cm žiadnym smerom.

Odkazy

1. Walter J. Moore. (1963). Fyzikálna chémia. V chemickej kinetike. Štvrté vydanie, Longmans.
2. Irán. Levine. (2009). Princípy fyzikálneho spôsobu. Šieste vydanie. MC Graw Hill.
3. Úvod do vedy o materiáloch a inžinierstve. (11. marca 2018). Fickov druhý zákon. Profesor. Rajesh Prasad. [Video]. Obnovené z: YouTube.com
4. Wikipedia. (2020). Fickove zákony difúzie. Zdroj: In.Wikipedia.orgán
5. Laura Dickson. (10. september 2020). Rozptýlenie. Chémia librettexts. Získané z: Chem.Librettexts.orgán
6. Larissa Zhou a kol. (1. september 2015). Pochopenie teórie difúzie a Fickov zákon prostredníctvom jedla a varenia. Americká fyziologická spoločnosť. doi.org/10.1152/Advan.00133.2014