Charakteristiky divergentných šošoviek, prvky, typy, aplikácie

Ten divergentné šošovky sú tie, ktoré sú tenšie v jej strednej a silnejšej časti na okrajoch. V dôsledku toho oddeľujú (odlišujú) svetelné lúče, ktoré ich ovplyvňujú paralelne s hlavnou osou. Ich rozšírenia nakoniec zbiehajú v zaostrovacom obrázku umiestnenom vľavo od objektívu.

Divergentné alebo negatívne šošovky, ako sú známe, tvoria to, čo sa nazýva virtuálne obrazy objektov. Majú rôzne aplikácie. Najmä v Ophtamológii sa používajú na korekciu krátkozrakosti a niektorých typov astigmatizmu.

Randrijo87 [CC BY-SA 4.0 (https: // creativeCommons.Org/licencie/By-SA/4.0)]

Takže, ak trpíte krátkozrakosťou a nosením okuliarov, máte dokonalý príklad divergentnej šošovky.

[TOC]

Charakteristiky divergentných šošoviek

Ako je uvedené vyššie, divergentné šošovky sú užšie vo svojej ústrednej časti ako na okrajoch. Okrem toho v tomto type šošoviek je jeden z jej povrchov vždy konkávny. To dáva tomuto typu šošoviek sériu charakteristík.

Na začiatok, predĺženie lúčov, ktoré ich ovplyvňujú. Je to tak preto, že lúče, ktoré prechádzajú cez šošovku, sa v žiadnom okamihu nekonvergujú, pretože sa líšia vo všetkých smeroch. Okrem toho v závislosti od zakrivenia šošovky sa lúče otvoria vo väčšej alebo menšej miere.

Ďalšou dôležitou črtou tohto typu šošoviek je to, že zameranie je vľavo od objektívu, takže je medzi tým a objektom.

Okrem toho sú v divergentných šošovkách obrázky menšie ako objekt a sú medzi týmto a zameraním.

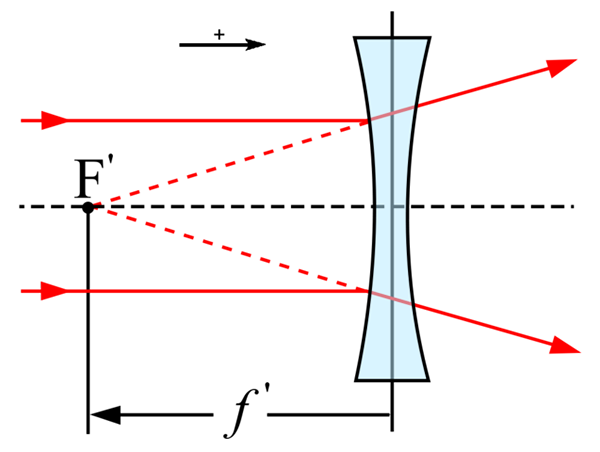Jipaul / z Henrika [CC BY-SA 3.0 (https: // creativeCommons.Org/licencie/By-SA/3.0)]

Prvky divergentných šošoviek

Pri ich štúdiu je nevyhnutné vedieť, aké prvky tvoria šošovky všeobecne a najmä odlišné šošovky.

Nazýva sa to optické centrum šošovky do bodu, prostredníctvom ktorého lúče nezažívajú žiadnu odchýlku. Na druhej strane hlavnou osou je čiara, ktorá sa pripojí k tomuto bodu a hlavným zameraním, ktorá je zastúpená písmenom F.

Môže vám slúžiť: zdroj napätia

Hlavné zameranie dostáva bod, v ktorom sa nachádzajú všetky lúče, ktoré ovplyvňujú objektív paralelne s hlavnou osou.

Týmto spôsobom sa vzdialenosť medzi optickým centrom a zameraním nazýva ohnisková vzdialenosť.

Centrá zakrivenia sú definované ako centrá sfér, ktoré vytvárajú šošovku; Týmto spôsobom rádiá zakrivenia rádiá sféry, ktoré vedú k šošovke. A nakoniec, centrálna rovina šošovky sa nazýva optická rovina.

Tvorba obrazu

Ak chcete grafovať tvorbu obrázka v tenkej šošovke, je potrebné len poznať smer, ktorý budú nasledovať dva z troch lúčov
ktorého trajektória je známa.

Jeden z nich je ten, ktorý ovplyvňuje objektív paralelne s optickou osou šošovky. Toto, akonáhle sa v objektívu prepadne, prejde obrazom zaostrenia. Druhý z lúčov, ktorých trajektória je známa, je ten, ktorý prechádza optickým centrom. To neuvidí upravená jej trajektória.

Tretí a posledný je ten, ktorý prechádza zaostrením objektu (alebo jeho predĺženia prechádza zaostrenie objektu), ktorý po prefakovaní bude nasledovať smer rovnobežne s smerom optickej osi šošovky.

Týmto spôsobom sa vo všeobecnosti bude vo šošovkách tvoriť typ obrazu alebo iného v závislosti od polohy objektu alebo tela vzhľadom na šošovku.

Avšak v konkrétnom prípade divergentných šošoviek, bez ohľadu na polohu tela pred šošovkou, bude mať obraz, ktorý sa vytvorí. A v divergentných šošovkách bude obraz vždy virtuálny, menší ako telo a vpravo.

Môže vám slúžiť: číslo toku: Ako sa vypočíta a príklady

Žiadosti

Skutočnosť, že môžu oddeliť svetlo, ktoré ich prechádza, dáva divergentné šošovky niektoré zaujímavé vlastnosti v oblasti optiky. Týmto spôsobom môžu opraviť krátkozrakosť a niektoré špecifické typy astigmatizmu.

Divergentné oftalmické šošovky oddeľujú lúče svetla, takže keď sa dostanú k ľudskému oku, sú vzdialenejšie. Keď teda prechádzajú rohovkou a šošovkou, ktoré idú ďalej a môžu dosiahnuť sietnicu, ktorá vedie problémy s zrakom ľudí, ktorí trpia krátkozrakosťou.

Chlapci

Ako sme už spomenuli, konvergentné šošovky majú aspoň jeden konkávny povrch. Z tohto.

Divergentné šošovky Bicócavas sa tvoria z dvoch konkávnych povrchov, planknas majú konkávny a rovný povrch, zatiaľ čo v konvexnom devergentnom menisku povrch je povrch mierne vypuklý a druhý je konkávny.

Rozdiely s konvergentnými šošovkami

V konvergentných šošovkách, na rozdiel od toho, čo sa deje v divergencii, hrúbka klesá zo stredu na hrany. V tomto type šošovky sú teda svetelné lúče, ktoré ovplyvňujú hlavnú os paralelne. Týmto spôsobom vždy vytvárajú skutočné obrázky objektov.

V optike sa konvergentné alebo pozitívne šošovky používajú hlavne na korekciu ďalekozrakosti, presbyopie a niektorých typov astigmatizmu.

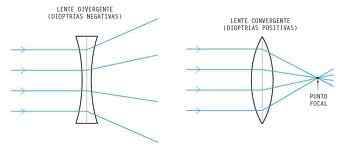GrantExGator [CC BY-SA 3.0 (https: // creativeCommons.Org/licencie/By-SA/3.0)]

Gaussova rovnica šošoviek a zvýšená šošovka

Typ šošovky, ktorý sa najčastejšie študuje, sa nazývajú tenké šošovky. Takto sú definované všetky šošovky, ktorých hrúbka je veľmi malá v porovnaní s rádiami zakrivenia povrchov, ktoré ich obmedzujú.

Štúdium tohto typu šošoviek sa môže vykonávať hlavne prostredníctvom dvoch rovníc: Gaussovu rovnicu a rovnicu, ktorá umožňuje určiť zvýšenie šošovky.

Gaussová rovnica

Dôležitosť Gaussovej rovnice tenkých šošoviek spočíva vo veľkom počte základných optických problémov, ktoré umožňujú vyriešenie. Váš výraz je nasledujúci:

Môže vám slúžiť: eliptické galaxie: formovanie, charakteristiky, typy, príklady

1/f = 1/p +1/q

Kde 1/ f je sila šošovky a F je ohnisková vzdialenosť alebo vzdialenosť od optického stredu k Focamu. Jednotka miery výkonu šošovky je diopter (d), čo predstavuje hodnotu 1 d = 1 m^-1. Na druhej strane sú p a q, respektíve vzdialenosť, v ktorej je objekt a vzdialenosť, ku ktorej je pozorovaný jeho obraz.

Cvičenie

Telo je umiestnené 40 centimetrov od divergentnej šošovky -40 centimetrov ohniskovej vzdialenosti. Vypočítajte výšku obrázka, ak je výška objektu 5 cm. Tiež určte, či je obrázok správny alebo obrátený.

Máme nasledujúce údaje: h = 5 cm; P = 40 cm; F = -40 cm.

Tieto hodnoty sa nahradia v Gaussovej rovnici tenkých šošoviek:

1/f = 1/p +1/q

A získa sa:

1/-40 = 1/40 +1/q

Kde q = - 20 cm

Ďalej nahradíme výsledok predtým získaný v rovnici zvýšenia šošovky:

M = - q / p = -20 / 40 = 0,5

Získanie, že hodnota zvýšenia je:

M = h '/h = 0,5

Vymazanie tejto rovnice H ', čo je hodnota výšky obrázka, dosahuje:

H '= h/2 = 2,5 cm.

Výška obrazu je 2.5 cm. Okrem toho je obrázok správny, pretože m> 0 a znížené, pretože absolútna hodnota M je menšia ako 1.

Odkazy

1. Svetlo (n.d.). Na Wikipédii. Z toho 11. apríla 2019.Wikipedia.orgán.
2. Lekner, John (1987). Teória reflexie, elektromagnetických a partelových vĺn. Prubár.
3. Svetlo (n.d.). Na Wikipédii. Získané 11. apríla 2019 z.Wikipedia.orgán.
4. Objektív (n.d.). Na Wikipédii. Z toho 11. apríla 2019.Wikipedia.orgán.
5. Objektív (optika). Na Wikipédii. Získané 11. apríla 2019 z.Wikipedia.orgán.
6. Acts, Eugene (2002). Optika (4. vydanie.). Addison Wesley.
7. Tupler, Paul Allen (1994). Fyzický. 3. vydanie. Barcelona: obrátil som sa.