Multiplikatívne inverzné vysvetlenie, príklady, cvičenia vyriešené
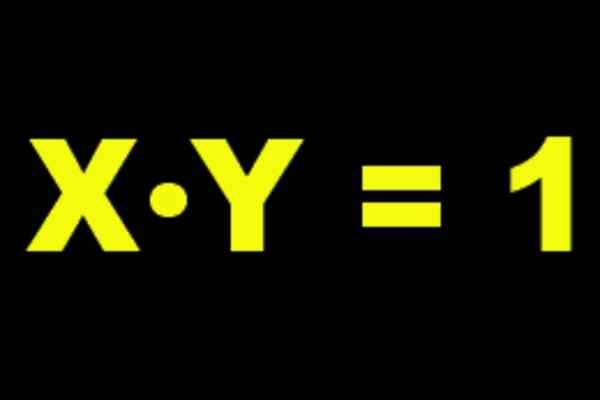
- 1387
- 235
- Adrián Fajnor
Rozumie to Inverzný multiplikačný jedného čísla, ďalšie číslo, ktoré sa vynásobí prvými výsledkami v neutrálnom prvku produktu, to znamená jednotka. Ak máte skutočné číslo do potom je jeho multiplikatívna inverzia označená do-1, A je splnené, že:
a-1 = a-1 A = 1
Zvyčajne číslo do Patrí do súboru skutočných čísel.
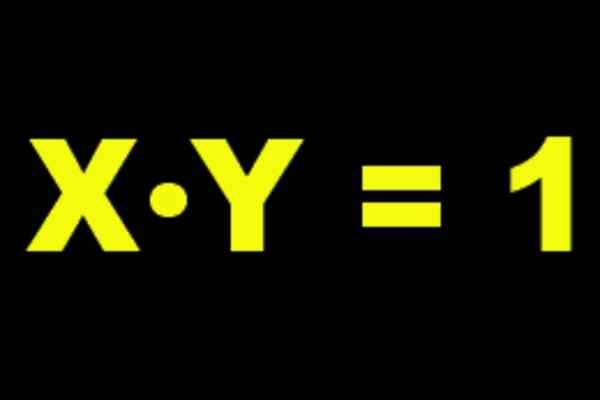 postava 1. A je to inverzná multiplikatívna z x a x je multiplikatívna inverzia y.
postava 1. A je to inverzná multiplikatívna z x a x je multiplikatívna inverzia y. Ak napríklad berieme A = 2, Potom je vaša multiplikatívna inverzia 2-1 = ½ Pretože sa overuje toto:
2 ⋅ 2-1 = 2-1⋅ 2 = 1
2lek ½ = ½ ⋅ 2 = 1
Do Inverzný multiplikačný čísla sa tiež nazýva recipročný, Pretože multiplikatívna inverzia sa získa výmenou čitateľa a menovateľa, napríklad multiplikatívna inverzia 3/4 je 4/3.
Spravidla sa dá povedať, že pre racionálne číslo (P/q) Vaša multiplikatívna inverzia (p/q)-1 Je to recipročné (Q/p) Ako je možné overiť nižšie:
(p/q) ⋅ (p/q)-1 = (p/q) ⋅ (q/p) = (p⋅ q)/(qrem p) = (p zajtra q)/(p⋅ q) = 1
Multiplikatívna inverzia neexistuje v číselnom súbore celých čísel, Napríklad, ak sa odoberie celé číslo 2, jeho multiplikatívna inverzia podľa toho, čo bolo uvedené vyššie, by bolo ½, ale ½ nie je celé číslo.
Existuje tiež multiplikatívna inverzia nulového prvku násobenia. Inými slovami, nulové číslo (0), ktoré je nulovým prvkom multiplikačnej operácie, nemá multiplikatívnu inverziu, pretože neexistuje žiadne číslo, ktoré sa vynásobí nulou jednotky.
Multiplikatívna inverzia existuje v racionálnych číslach, v reálnych číslach a zložitých číslach.
Multiplikatívne inverzné príklady
Príklad 1
Nájdite multiplikatívnu inverziu 3/2 a overte, či spĺňa vlastnosť multiplikatívnych celých čísel.
Môže vám slúžiť: Coplanares body: rovnica, príklad a vyriešené cvičeniaPodľa vyššie uvedeného pravidla sa multiplikatívna inverzia (3/2) je (2/3) vymenená týmto spôsobom. Na overenie sa vykonáva násobenie týchto dvoch čísel:
(3/2) ⋅ (2/3) = (3 ⋅ 2)/(2 ⋅ 3) = 6/6 = 1.
Ak chcete vynásobiť dve frakčné čísla, jednoducho vynásobte čitateľa prvého druhým čitateľom, aby ste získali výsledný čitateľ.
Na získanie menovateľa produktu frakčných čísel, postupujte podobným spôsobom, to znamená, že menovatelia sa navzájom vynásobia a výsledkom je menovateľ produktu. V našom príklade sa overuje, že čitateľ produktu čísla a jeho recipročného je 6 a menovateľ je 6, pričom frakcia 6/6 ponecháva 1, čo je 1.
Príklad 2
Multiplikatívna inverzia -5 by sa nemala zamieňať so svojou symetrickou (+5), ktorá sa niekedy nazýva aritmetická inverzia. Multiplikatívna inverzia sa získa takto:
(-5) ⋅ x = 1
Kde x je multiplikatívna inverzná, ktorá sa má získať. Možný postup spočíva v vyčistení neznámeho x. AS (-5) vynásobí neznáme X v ľavom členovi, potom sa stáva delením správneho člena:
X = 1 / (-5)
Ako je známe + medzi - je to - potom sa konečne získa x:
X = - ⅕ .
Na záver - ⅕ je multiplikatívna inverzia -5.
Príklad 3
Získajte multiplikatívnu inverziu -√2. Predpokladajme, že multiplikatívna inverzia je x, potom -√2 vynásobená x musí byť jednotka, podmienka, ktorú ukladáme nižšie:
-√2 ⋅ x = 1
Obaja členovia sú rozdelení -…2 na získanie:
)
Prvý člen je zjednodušený -„Zostávajúce:
Môže vám slúžiť: Štandardná chyba odhadu: Ako sa vypočítava, príklady, cvičeniaX = 1 / (-√2)
Tento výraz možno racionalizovať, to znamená, že eliminuje koreň menovateľa, ktorý sa vynásobí v čitateľovi (-√2) a v menovateľovi pre rovnaké množstvo, aby sa výsledok nezmenil:
X = (-√2) / [(-√2) (-√2)] =-(√2 / 2)
Záverom - (√2/2) je multiplikatívna inverzia (-√2).
Príklad 4
Predpokladajme akékoľvek číslo X, získajte svoju multiplikatívnu inverziu a graficky ho reprezentujte.
V tomto prípade ide o funkciu f (x) = x, získanie multiplikatívnej inverzie je nájsť funkciu g (x) tak, aby sa vynásobil prvou jednotkou jednotky. Funkcia G je recipročná funkcia F a nemala by sa nijako zamieňať s jeho inverznou funkciou.
Inými slovami, multiplikatívna inverzia X je A a taká, že sa splní nasledujúce:
x ⋅ y = 1
Kde vyčistiť a mať:
y = 1/x.
Vyššie uvedené sa takto interpretuje vzhľadom na hodnotu x, predchádzajúci vzorec nám dáva jeho multiplikatívnu inverziu.
Je možné dosiahnuť grafické znázornenie, ako je to znázornené na nasledujúcom obrázku:
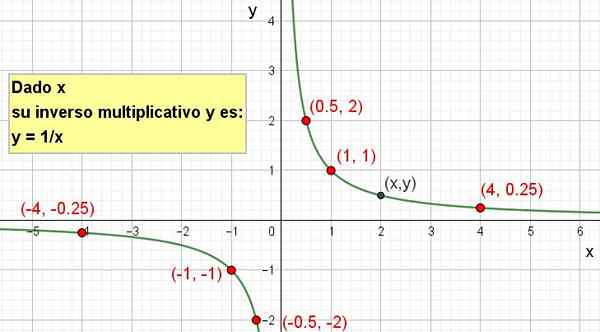 Obrázok 2. Multiplikatívna inverzia x je y = 1/x.
Obrázok 2. Multiplikatívna inverzia x je y = 1/x. Cvičenia
Cvičenie 1
Vzhľadom na x = 2 - √2, získajte svoju multiplikatívnu inverziu a.
Riešenie:
Takže a je to multiplikačný x x
x ⋅ y = 1
X je nahradený jeho hodnotou:
(2 - √2) ⋅ y = 1
Potom to vymaže a:
y = 1 / (2 - √2)
Racionalizácia výsledku vynásobí čitateľa a menovateľa jeho konjugovaným binomiálnym prúdom:
y = (2 + √2) / ((2 + √2) (2 - √2))
U menovateľa sa uznáva pozoruhodný produkt nazývaný produkt súčtu pre rozdiel, čo je rozdiel štvorcov. Týmto spôsobom koreň zmizne v menovateľovi.
y = (2 + √2) / (2^2 - (√2)^2)
Môže vám slúžiť: PomerRiešenie právomocí:
y = (2 + √2) / (4 - 2)
Zjednodušenie:
y = (2 + √2) / 2
Cvičenie 2
Získajte multiplikatívnu inverziu (1/a + 1/b), kde a a b sú rôzne reálne čísla.
Riešenie:
Voláme a multiplikatívnu inverziu (1/a + 1/b), takže je potrebné splniť nasledujúcu rovnicu:
A ⋅ (1/a + 1/b) = 1
Premenná je vyčistená a:
Y = 1/(1/a + 1/b)
Menovateľ je vyriešený:
Y = 1 / ((b + a) / a b)
Ako je známe o pravidlách algebry, menovateľ menovateľa prechádza čitateľovi:
Y = (a b) / (b + a)
Je nariadené, aby sa konečne získalo:
(a b)/(a + b), čo je multiplikatívna inverzia (1/a + 1/b).
Cvičenie 3
Získajte multiplikatívnu inverziu (a - b) / (a^2 - b^2).
Riešenie:
Pripomeňme, že multiplikatívna inverzia sa tiež nazýva recipročná, pretože sa získava iba výmena čitateľa a menovateľa.
Potom bude multiplikatívna inverzia (a - b) / (a^2 - b^2):
(A^2 - b^2) / (a - b)
Tento výraz sa však dá zjednodušiť, ak si podľa pravidiel algebry uvedomíme, že čitateľ je rozdielom štvorcov, ktoré možno faktorovať ako produkt súčtu pre rozdiel:
((A + b) (a - b)) (a - b)
Pretože v čitateľovi a menovateľovi existuje spoločný faktor (a - b), pokračujeme v zjednodušení, nakoniec získaní:
(a + b) čo je multiplikatívna inverzia (a - b) / (a^2 - b^2).
Odkazy
- Zdroje, a. (2016). Základná matematika. Úvod do výpočtu. Luk.com.
- Garo, m. (2014). Matematika: Kvadratické rovnice: Ako vyrieši kvadratickú rovnicu. Marilù garo.
- Haeussler, e. F., & Paul, r. Siež. (2003). Matematika pre správu a ekonomiku. Pearson Vzdelanie.
- Jiménez, J., Rofríguez, m., & Estrada, r. (2005). Matematika 1 september. Prah.
- Vzácny, c. Tón. (2005). Kurz matematiky 3o. Redakčný progreso.
- Rock, n. M. (2006). Algebra I je ľahká! Tak ľahké. Tímová rocková tlač.
- Sullivan, J. (2006). Algebra a trigonometria. Pearson Vzdelanie.

