Vzorce magnetickej indukcie, ako sa vypočítajú a príklady

Ten magnetická indukcia alebo hustota magnetického toku je zmena prostredia spôsobeného prítomnosťou elektrických prúdov. Upravujú povahu okolitého priestoru a vytvárajú a lúka Vektor.

Vektor Magnetická indukcia, hustota magnetického toku Alebo jednoducho magnetické pole B, Má tri výrazné charakteristiky: intenzita vyjadrená numerickou hodnotou, adresa a tiež zmysel uvedený v každom bode vesmíru. Zvýrazňuje sa tučným písmom, aby sa odlíšil od čisto číselných množstiev alebo skalárnych.

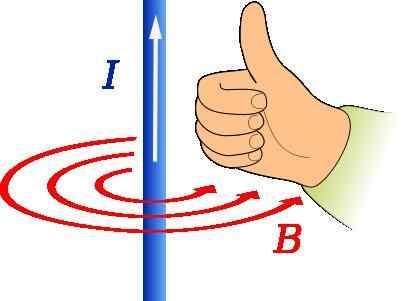Pravidlo pravého palca na určenie smeru a smeru magnetického indukčného vektora. Zdroj: JFMelero [CC BY-SA 4.0 (https: // creativeCommons.Org/licencie/By-SA/4.0)]

Pravidlo pravého palca sa používa na nájdenie smeru a smeru magnetického poľa vzniknutého vodičom, ktorý transportuje prúd, ako je znázornené na obrázku vyššie.

Palec pravej ruky by mal smerovať smerom k prúdu. Potom nalom zostávajúcich prstov naznačuje formu B, že na obrázku je reprezentované koncentrickými kruhmi červenej.

V tomto prípade adresa B Je tangenciálny k sústrednému obvodu s drôtom a význam je v rozpore s hodinovými rukami.

Ten magnetická indukcia B V medzinárodnom systéme sa meria Tesla (T), je však bežnejšie zmerať ho v inej jednotke s názvom Gauss (G). Obe jednotky boli vymenované na počesť Nikola Tesly (1856-1943) a Carl Friedrich Gauss (1777-1855) za ich mimoriadne príspevky k vede o elektrine a magnetizme.

[TOC]

Aké sú vlastnosti magnetickej indukcie alebo hustoty magnetického toku?

Kompas, ktorý je umiestnený v blízkosti drôtu so prúdom, sa vždy zarovná s B. Dánsky fyzik Hans Christian Oersted (1777-1851) bol prvým, kto si tento jav uvedomil na začiatku 19. storočia.

Môže vám slúžiť: Areolar Speed: Ako sa vypočítava a vyrieši

A keď súčasný prestane, kompas ukazuje na geografický sever, ako vždy. Opatrnou zmenou polohy kompasu sa mapa získa z tvaru magnetického poľa.

Táto mapa má vždy formu koncentrických kruhov k drôtu, ako je opísané na začiatku. Týmto spôsobom sa dá vizualizovať B.

Aj keď drôt nie je rovný, vektor B bude okolo neho tvoriť koncentrické kruhy. Aby sa určilo, akú formu má pole, stačí si predstaviť veľmi malé segmenty drôtov, ktoré sa zdajú byť priamočiare a obklopené sústrednými obvodmi.

Magnetické polia vedenia produkované drôtenou slučkou, ktorá prepravuje prúd. Zdroj: Pixabay.com

To naznačuje dôležitú vlastnosť riadkov magnetického poľa B: Chýbajú im princíp alebo koniec, vždy sú to zatvorené krivky.

Zákon o biote-savart

19. storočie určilo začiatok éry elektriny a magnetizmu vo vede. V roku 1820 francúzski fyzici Jean Marie Biot (1774-1862) a Felix Savart (1791-1841) objavili zákon, ktorý nesie jeho meno a ktorý umožňuje výpočet vektora B.

Urobili nasledujúce pozorovania o príspevku do magnetického poľa vytvoreného segmentom drôtovej dĺžky diferenciálov DL ktorý prepravuje elektrický prúd Jo:

• Veľkosť B klesá s inverziou na štvorcový vzdialenosť od drôtu (to dáva zmysel: ďaleko od drôtu intenzita intenzity B Musí to byť menej ako v blízkych bodoch).
• Veľkosť B Je úmerný intenzite prúdu Jo ktoré cestuje na drôte.
• Adresa B Je to tangenciálne k obvodu rádiu r stredom na drôte a smer B Ako sme povedali, je uvedené pravidlom pravého palca.

Vektorový alebo produktový krížový produkt je vhodným matematickým nástrojom na vyjadrenie posledného bodu. Na vytvorenie vektorového produktu sú potrebné dva vektory, ktoré sú definované takto:

• dl Je to vektor, ktorého veľkosť je dĺžka diferenciálneho segmentu DL
• r Je to vektor, ktorý prechádza z drôtu do bodu, kde chcete nájsť pole

Môže vám slúžiť: elektromagnetické spektrum: Charakteristiky, pásma, aplikácie

Vzorce

To všetko sa dá kombinovať v matematickom výraze:

Konštanta proporcionality potrebná na stanovenie rovnosti je Magnetická priepustnosť voľného priestoru μ_ani  = 4π.10^-7 Tón.m/a

Tento výraz je Biot a Savartov zákon, ktorý vám umožňuje vypočítať magnetické pole aktuálneho segmentu.

Takýto segment musí byť zase súčasťou väčšieho a väčšieho obvodu: Distribúcia prúdu.

Podmienka, že obvod je uzavretý, je potrebný na prietok elektrického prúdu. Elektrický prúd nemôže prúdiť v otvorených obvodoch.

Nakoniec, aby ste našli celkové magnetické pole tohto súčasného rozdelenia, pridajú sa všetky príspevky každého diferenciálneho segmentu dl. Toto je rovnocenné s integráciou všetkého distribúcie:

Ak chcete uplatniť zákon Biot-Savart a vypočítať vektor magnetickej indukcie, je potrebné zvážiť veľmi dôležité dôležité body:

• Vektorový produkt medzi dvoma vektormi vždy vedie k inému vektorovi.
• Rozsah vektorového produktu v zákone Biot-Savart je:kde θ je uhol medzi dl a r.
• Mal by sa nájsť vektorový produkt pred Ak je integrálne rozlíšenie vyriešené, potom je integrál každej z komponentov získaných osobitne vyriešený.
• Je potrebné nakresliť situáciu a vytvoriť primeraný súradnicový systém.
• Kedykoľvek sa pozoruje existencia nejakej symetrie, musí sa použiť na uloženie času výpočtu.
• Ak existujú trojuholníky, veta Pythagoras a Cosine Terem veľmi pomáhajú nadviazať geometrický vzťah medzi premennými.

Ako sa vypočítava?

S praktickým príkladom výpočtu B Pre priamy drôt sa tieto odporúčania používajú.

Môže vám slúžiť: Presné zaťaženie: Vlastnosti a zákon Coulomb

Príklad

Vypočítajte vektor magnetického poľa, ktorý veľmi dlhý rektilový drôt produkuje v bode p priestoru, podľa zobrazeného obrázku.

Geometria potrebná na výpočet magnetického poľa v bode P, nekonečne dlhého prúdového drôtu. Zdroj: Self Made.

Z čísla, ktorú musíte:

• Drôt je nasmerovaný vertikálne, pričom prúd tečiem hore. Táto adresa je +a v súradnicovom systéme, ktorého pôvod je v mieste alebo.
• θ je uhol medzi dl a r A je tiež pravda, že: 
• V tomto prípade podľa pravidla pravého palca, B V bode P je nasmerovaný do papiera, takže je označený malým kruhom a „x“ na obrázku. Táto adresa sa považuje za -z.
• Pravý trojuholník, ktorého nohy sú a a R, Vzťahuje obe premenné podľa vety Pythagoras: r²= R²+a²

To všetko sa nahradí v integráli. Vektor alebo krížový produkt je označený jeho veľkosťou plus smerom a významom:

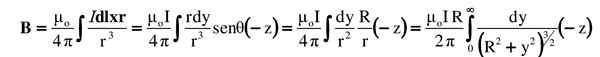
Navrhovaný integrál sa hľadá v integrálnej tabuľke alebo je vyriešený vhodnou trigonometrickou substitúciou (čitateľ môže skontrolovať výsledok pomocou y = rtg 9):

Výsledok súhlasí s očakávanými: veľkosť poľa klesá so vzdialenosťou R a proporcionálne sa zvyšuje s intenzitou prúdu i.

Zatiaľ čo nekonečne dlhý drôt je idealizácia, získaný výraz je veľmi dobrý prístup k poľu dlhého drôtu.

S zákonom o biote a savart je možné nájsť magnetické pole iných distribúcií s vysokou symetriou, ako je kruhová špirála, ktorá prepravuje prúd alebo zložené drôty kombinujúce priamočiare a krivočiare segmenty.

Aby sa analyzovala integrálny, musí mať problém vysoký stupeň symetrie. Inak alternatívou je numerické riešenie integrálu.

Odkazy

1. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 2. Mexiko. Redaktori učenia sa Cengage. 367-372.