Matematická rovnosť
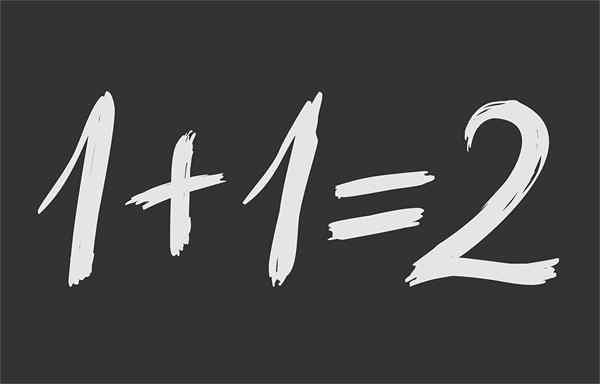
- 4242
- 137
- Tomáš Mydlo
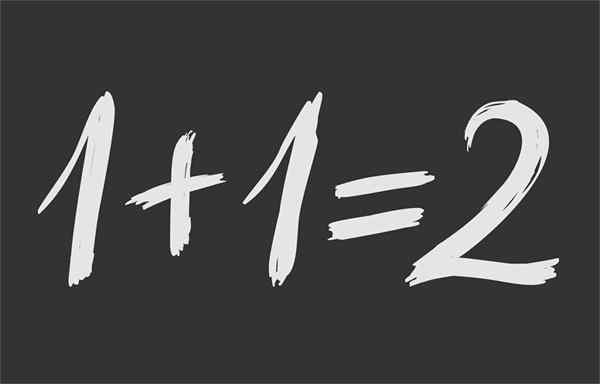 postava 1.- Matematická rovnosť zaisťuje, že 1 + 1 je rovnaká 2
postava 1.- Matematická rovnosť zaisťuje, že 1 + 1 je rovnaká 2 Čo je matematická rovnosť?
Matematická rovnosť zaisťuje, že dva výrazy sú rovnaké alebo odlišné, sú úplne rovnocenné. Tieto výrazy môžu byť rozmanité, napríklad čísla, písmená, ktoré symbolizujú množstvá alebo veľkosti, kombinácie čísel a písmen, matíc a ďalších.
Symbol používaný na označenie rovnosti v matematickom jazyku je stav dvoch paralelných a vodorovných riadkov, ktoré v tlačenom texte sú dobre známym symbolom "=". Napríklad, ak máte tri jablká, môžete napísať nasledujúcu rovnosť:
Počet jabĺk = 3
Fráza „Počet jabĺk“ je členom ľavej strany a číslo 3 je členom napravo od rovnosti.
Pretože je možné písať číselné sumy rôznymi spôsobmi, rovnosť sa používa na ich označenie. Pri konkrétnom prípade na ilustráciu tohto bodu existuje niekoľko spôsobov, ako napísať číslo 4, okrem tých najzreteľnejších, čo je 4 = 4, je možné napísať nasledujúce prostredníctvom matematickej rovnosti:
2 + 2 = 4
6 - 2 = 4
8 ÷ 2 = 4
2 × 2 = 4
22 = 4
Tu zobrazená rovnosť je pravdivá, ale rovnosť nemusí byť, napríklad 10 + 5 = 20 je nepravdivá, pretože 10 + 5 = 15.
Čitateľ určite pozná iné spôsoby, ako napísať číslo 4. Všimnite si, že výrazy na každej strane rovnosti môžu byť čísla, slová, písmená, ktoré symbolizujú sumy alebo iné symboly, napríklad:
x + 1 = 7
do2B - 1 = xy
f (x) = 2x2
Matematici nepoužívali vždy symbol rovnosti, takže staré matematické zmluvy boli veľmi rozsiahle.
Pripisuje sa matematikovi a doktorovi Robertovi Pamätam (1510-1558), narodený vo Walese, vytvorenie symbolu rovnosti „=“, tak známe všetkým dnešným dneškom. Pamätajte si, že je zjavne unavený z písania frázy „Rovnako ako“ v jednej z jeho matematických zmlúv, rozhodol sa namiesto toho skrátiť príbuzné paralelné pruhy.
Môže vám slúžiť: Pentagonálny hranol: Charakteristiky, časti, vrcholy, hrany, objemVlastnosti matematickej rovnosti
Nasledujúce vlastnosti umožňujú správne pracovať s matematickou rovnosťou. Sú axiomatickí, takže nevyžadujú demonštráciu:
1.- Reflexný majetok
Táto vlastnosť ustanovuje, že akákoľvek suma sa rovná sebe samému. Najmä, pretože akékoľvek číslo sa rovná sebe samému, je možné napísať rovnaké:
5 = 5
36.35 = 36.35
Ak je suma doslovná alebo je to kombinácia písmen a čísel, rovná sa aj sebe:
3x = 3x
do2Bc-1 = a2Bc-1
2.- Vlastnosť symetrie
Sumy alebo členovia na oboch stranách rovnosti sa môžu vymeniť bez stratenej platnosti. To znamená, že ak je to, čo je vľavo od symbolu „=“, napísané po vašej pravici a čo je po vašej pravici, je umiestnené vľavo, je to rovnaká rovnosť.
Napríklad expresia 5 + 2 = 7 je ekvivalent tomuto: 7 = 5 + 2. Rovnakym sposobom:
12 + 8 = 20; 20 = 12 + 8
x + 1 = 3; 3 = x + 1
x - z = y; y = x - z
3.- Prekladací majetok
Táto vlastnosť sa vzťahuje na rovnocennosť rovnosti. Ak majú dve rovnosť spoločného člena, potom sú tiež rovnaké, pretože všeobecne:
Ak „x = y“ a „y = z“, potom x = z
Na ilustráciu tejto vlastnosti zvážte tieto dve číselné rovnosti: 2 + 2 = 4 a 6 - 2 = 4. Pretože obidve sa rovnajú 4 (majú spoločného člena), potom je možné napísať nasledujúce, bez straty akejkoľvek platnosti:
2 + 2 = 6 - 2
Ďalší príklad, tentoraz s písmenami:
Áno x + 1 = 5
A
A - B = 5
Tak:
x+1 = a - b
4.- Zhoršenie
Rovnosť sa nezmení, ak v oboch členoch existuje rovnaká suma, ktorá pridáva (alebo odpočítava) a rozhodne sa to vylúčiť alebo zrušiť toto. Toto je zrušovacia vlastnosť sumy.
Zoberme si príklad nasledujúcu numerickú rovnosť, v ktorej sa 10 objaví v prísahe, ako aj v ľavej ľavej strane:
Môže vám slúžiť: trigonometrické funkcie: Základné, v karteziánskej rovine, príklady, cvičenie2 + 2 + 10 = 6 - 2 + 10
Číslo 10 sa dá zrušiť bez toho, aby stratila svoju platnosť, zostala ďalšia kratšia rovnosť a ekvivalent k predchádzajúcemu:
2 + 2 = 6 - 2
V rovnosti (10 ÷ 2) - 3 = 5 - 3 celé číslo - 3 patrí obom členom rovnosti a javí sa ako pridanie, preto je možné zrušiť a získať:
10 ÷ 2 = 5
Stáva sa to tiež s doslovnými množstvami, napríklad:
Áno x + 2y + z = −a + b + z
Potom je možné zrušiť „z“, pretože sa nachádza na oboch stranách rovnosti ako pridanie (as rovnakým znakom).
Týmto výsledkom je:
x + 2y = −a + b
Môže tiež definovať zrušovaciu vlastnosť násobenia. Ak rovnaká suma C vynásobí oboch členov rovnosti, môže byť táto suma zrušená napríklad:
Cx = cy
Potom je možné C zrušiť, aby sa získalo jednoducho:
x = y
5.- Uniformita
Rovnosť zostáva nemenná pridaním, odpočítaním, vynásobením alebo delením rovnakým množstvom na oboch stranách toho istého.
Napríklad musí na 8 + 5 = 13, ak obaja členovia vynásobia určité ľubovoľné číslo C = 2, rovnosť zostáva:
(8+5) × 2 = 13 × 2
13 × 2 = 26
Matematické rovnaké triedy
Existujú rôzne typy matematickej rovnosti, takže sú klasifikované pre ich najlepšie porozumenie v:
-Totožnosť, Sú to rovnosť, v ktorej sú obaja členovia identickí:
2 = 2
x = x
2x = x + x
a tak ďalej.
-Rovnicia, Toto sú rovnosti, v ktorých sa objaví jeden alebo viac neznámych a sú pravdivé pre určité hodnoty, to znamená, že rovnosť nie je splnená pre žiadnu svojvoľnú hodnotu, takže sú známe aj ako známe ako podmienka. Príklady:
x + 1 = 5
X3 = 27
A + B = 40
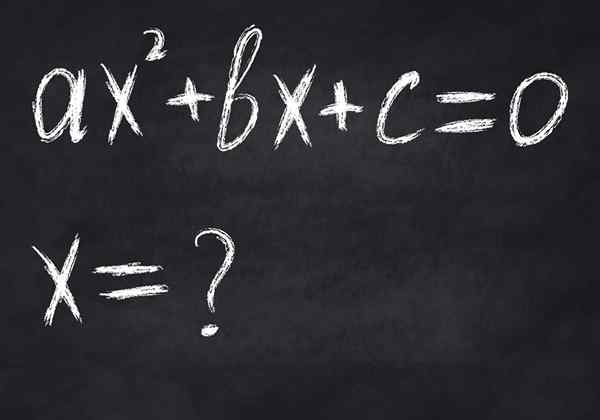 Obrázok 2.- Rovnica je podmienená matematická rovnosť, pretože je splnená iba pre určité premenné hodnoty. Obrázok zobrazuje rovnicu druhého stupňa, ktorá má nanajvýš dve skutočné riešenia
Obrázok 2.- Rovnica je podmienená matematická rovnosť, pretože je splnená iba pre určité premenné hodnoty. Obrázok zobrazuje rovnicu druhého stupňa, ktorá má nanajvýš dve skutočné riešenia -Rovnocennosť, V nich je člen ľavice rovnocenný s tým vpravo, aj keď nie sú rovní, napríklad v: 23 = 8.
Môže vám slúžiť: Aditívny princíp-Vzorce, Je to rovnosť, ktorá je vždy splnená pre hodnoty nezávislej premennej, ako v dobre známeho vzorca pre vzdialenosť D v závislosti od času t mobilu s rovnomerným priamkovým pohybom: D = v ∙ t
Vyriešené cvičenia
Cvičenie 1
Napíšte číslo 10 až štyri rôzne a ekvivalentné rovnosť.
Riešenie
Všetky tieto rovnosti expresné číslo 10, ale rôznymi spôsobmi:
5 × 2 = 10
11-1 = 10
101= 10
20 ÷ 2 = 10
Cvičenie 2
Aká je hodnota X, ktorá spĺňa rovnosť x + 1 = 3?
Riešenie
Táto rovnosť je rovnica, pretože hodnota X nie je známa. Ak je pridaný výraz X + 1 = 3, ak sa pridá výraz x + 1 = 3 (−1) na oboch stranách symbolu "=", rovnosť zostáva:
x + 1 + (−1) = 3 + ( - 1)
Pri pridávaní (−1) k členovi vľavo a operácii je vyriešená, „x“ je sám na ľavej strane rovnosti, tento postup sa nazýva odbavenie:
x + 1 - 1 = 3-1
x = 2
Preto hodnota, ktorá vyhovuje tejto rovnosti, je x = 2.
Cvičenie 3
Ak má mobil s rovnomerným priamym pohybom rýchlosť 2.5 m/s, aká je vzdialenosť, ktorá prebieha po 3 sekundách?
Riešenie
Používa sa vzorec v predchádzajúcej časti, D = v ∙ t, v ktorej sa nahradí hodnota V:
D = 2.5 ∙ t
Výraz sa stáva rovnosťou, keď t = 3 sekundy a operácia je vyriešená:
D = 2.5 ∙ 3 m = 7.5 m
Čo má za následok rovnosť:
D = 7.5 m
Odkazy
- Barnett, r. 2000. Predbežná časť. 4. Vydanie. McGraw Hill.
- Larson, R. 2012. Predbežná časť. 8. Vydanie. Učenie sa.
- Pérez, V. Vlastnosti algebraickej rovnosti. Obnovené z: matematiky.LAGUIA2000.com.
- Vlastnosti rovnosti. Zdroj: PPS.K12.Alebo.my.
- Stewart, J. 2007. Predklulácia: matematika na výpočet. 5. Vydanie. Učenie sa.

