Trigonometrické identity (príklady a cvičenia)

Ten trigonometrické identity Toto sú vzťahy medzi trigonometrickými dôvodmi, ktoré sú pravdivé pre akúkoľvek hodnotu premennej. Napríklad:

Tan θ = sin θ /cos θ

Je to trigonometrická identita, ktorá sa týka troch dôvodov uhla 9, tangens, prsníka a kosínus uvedeného uhla.

postava 1. Niektoré trigonometrické identity široko používané pri výpočte. Zdroj: f. Zapata.

Táto identita platí pre celú hodnotu, s výnimkou tých, ktoré robia 0 menovateľ. COS θ je 0 pre 9 = ± π/2, ± 3π/2, ± 5π/2… Ďalším príkladom trigonometrickej identity je:

hriech x . Sec x . CTG X = 1

[TOC]

Demonštrácia

Existujú dva základné spôsoby, ako preukázať, že trigonometrická identita je pravdivá:

1- transformácia jedného z členov rovnosti na druhého, prostredníctvom pohodlných algebraických manipulácií.

2- Rozvíjajte oboch členov rovnosti osobitne, až kým príslušné konečné výrazy každého z nich nie sú rovnaké.

V navrhovanej identite sa zmeníme ľavá strana rovnosti, pre ktorú vyjadrujeme CTG X a Sec X z hľadiska prsníka a kosínus nasledovne:

Ctg x = cos x / sen x

Sec x = 1 /cos x

Tento výraz nahradzujeme na ľavej strane identity a zjednodušujeme:

hriech x . (1/cos x). (cos x / sen x) = (sin x. cos x / cos x . hriech x) = 1

A pravdivosť identity sa už osvedčila.

Typy trigonometrických identít

Existuje niekoľko druhov trigonometrických identít. Ďalej stručne opíšeme tie hlavné:

- Základné trigonometrické identity

Rozlišujeme dva typy základných identít:

I) tie, ktoré sú vyjadrené prostredníctvom základných dôvodov, kosínus a tangens:

• Sec x = 1 /cos x
• Harm x / 1 / sin x
• Ctg x = 1 / tg x
• Tg x = sin x /cos x
• Ctg x = cos x / sen x

I) tie odvodené z parity. Prostredníctvom jeho grafu vieme, že Sen X je zvláštna funkcia, čo znamená, že:

Môže vám slúžiť: 60 deliteľov

sin (-x) = - sin x

Z tohto dôvodu je teda pár, preto:

cos (-x) = cos x

Tak:

tg (-x) = sen (-x) / cos (-x) = -sen x / cos x

Podobne:

• COTG (-x) = -ctg x
• sec (-x) = sec x
• Harm (-x) = - Harm x

- Pythagorské identity

Sú to tie získané z aplikácie vety Pythagoras na obdĺžnikový trojuholník mačiek A a B a hypotenusa c. Pozrime sa:

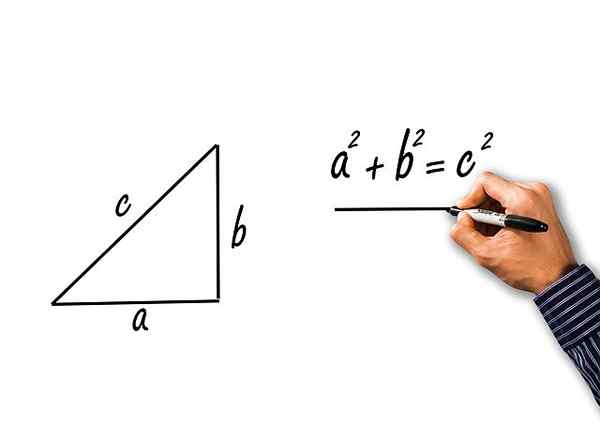Obrázok 2.- Z Pythagorasovej vety sa získajú tri pythagorské trigonometrické identity. Zdroj: Pixabay.

Pythagorasova veta uvádza, že:

c² = a² + b²

Rozdelenie všetkého medzi C²:

c² / c² = (a² / c²) + (B² / c²)

Termín vľavo je 1 a pamätá, že sínus a kosínus akútneho uhla α sú definované ako:

Sin α = A/C

cos α = b/c

Výsledok:

1 = (sin a)² + (cos α)²

Táto identita je známa ako základná identita.

Postup sa môže vykonať rozdelením medzi² a b², čo vedie k ďalším dvom identitám:

Sekundu² a = 1 + tg² α

haroghect² a = 1 + ctg² α

- Vzorce pre kosínus a prsník súčtu/odčítania uhlov

Hlavné trigonometrické identity pre kosínus, prsia a dotyčnicu súčtu a odčítania sú nasledujúce:

Demonštrácia Sen (a + β) a cos (a + β)

Tieto identity sa dajú demonštrovať geometricky alebo tiež prostredníctvom Eulerovho vzorca:

a^iA = cos a + i sin α

Pozrime sa, čo sa stane so vzorcom pri výmene súčtu dvoch uhlov α a β:

a^{I (α +p)} = cos (a + β) + i sin (a + β)

Táto expresia je zložitá, jej skutočná časť je cos (a + β) a jej imaginárna časť je I sin (a + β). Tento výsledok si ponecháme, aby sme ho použili neskôr a zamerali sa na rozvoj exponenciálnej časti:

a^{I (α +p)} = e^iA ⋅ E^ip = (cos a + i sin α) . (cos β + i sin β) =

Môže vám slúžiť: šesťuholníkový hranol

= cos α⋅cos β + cos α⋅I Sen β + i⋅sen α cos β - sen αsen β

Skutočná časť tohto výrazu je tá, ktorá nie je vynásobená imaginárnou jednotkou „I“:

cos α⋅cos β - sen α. Senátor

Imaginárna časť je preto:

I (cos a kedy β + sen a⋅cos β)

Aby boli dva komplexné výrazy rovnaké, skutočná časť jedného sa musí rovnať skutočnej časti druhej. To isté platí pre imaginárne časti.

Berieme výsledok uložený a porovnávame ho s týmto:

cos α. cos β - sen α. SIN β = cos (a + β)

I (cos a kedy β + sen a⋅cos β) = I sin (a + β)

sin (a + β) = (cos α. sin β + sen a⋅cos β)

- Vzorce pre dvojitý uhol

V predchádzajúcich vzorcoch berieme β = α a vyvíjame sa:

SIN (a + a) = sen 2 α = sen a+cos a + cos α. sin a = 2 šor

cos (a + a) = cos2 α = cos a Dobre² α - sen ² α

Tg (a + a) = Tg2 a = [Tg a + Tg a] / [1- Tg a kedy sa² α

Ak sa v druhom výraze vymenia cos² α = 1 - sen² α sa získa:

cos 2 α = cos² a- (1- cos² a) = 2 cos² α -1

- Polovičné vzorce

V tejto poslednej expresii nahrádzame a/2, zostáva nasledujúce:

cos α = 2 cos ²(a/2) -1

Vyčistenie:

Vyriešené cvičenia

- Cvičenie 1

Ukáž to:

Riešenie

Ideme pracovať algebraicky termín, ktorý zostal. Ako v pravom termíne sa javí Sen X, prvým krokom je vyjadriť cos²X Pokiaľ ide o sen X, takže všetko je z hľadiska rovnakého trigonometrického dôvodu:

Môže vám slúžiť: frakcia ekvivalentná 3/5 (riešenie a vysvetlenie)

Potom 1 - sen je faktor² x pre to, že je rozdiel v dokonalých štvorci. Za týmto účelom je to zrejmé zo základnej identity:

cos²X = 1 - sen² X

1 - sen² x = (1-sin x) (1+senx)

A faktorizácia v pôvodnom výraze sa nahradí:

Termín (1- senx) je zjednodušený a rovnosť zostáva:

1 + sen x = 1 + senx

- Cvičenie 2

Vyriešte nasledujúcu trigonometrickú rovnicu a uveďte riešenie pre hodnoty medzi 0 a 360 °:

TG X + SEC² x = 3

Riešenie

V ľavom období existujú dva trigonometrické dôvody, preto musíte zredukovať všetko na jeden, aby ste mohli vyčistiť neznáme. Termín SEC² X je vyjadrená prostredníctvom jednej z pythagorských identít:

Sekundu² a = 1 + tg² α

Nahradením rovnice:

TG X + 1 + TG² x = 3

Usporiadanie pojmov:

Tg² x + tg x + 1 = 3

Táto rovnica je vyriešená zmenou premennej:

tg x = u

alebo² + U + 1 - 3 = 0 → u² + U - 2 = 0

Táto rovnica druhého stupňa je ľahko vyriešená faktorizáciou:

(U +2) (u-1) = 0

Preto u₁ = -2 a u₂ = 1, ekvivalent:

Tg x₁ = -2

Tg x₂ = 1

Konečne:

X₁ = arctg (-2) = 296.6

X₂  = arctg (1) = 45 °

Odkazy

1. Carena, m. 2019. Príručka matematiky preduniverzity. Národná univerzita pobrežia.
2. Figuera, J. 1999. Matematika. 1. Diverzifikovaný. Bolivarian Collegiate Editions.
3. Hoffman, J. Výber matematických problémov. Zväzok 4.
4. Jiménez, r. 2008. Algebra. Sála.
5. Wikipedia. Identity a vzorce trigonometrie. Obnovené z: je.Wikipedia.orgán.
6. Zapata, f. 4 spôsoby, ako vyriešiť rovnicu druhého stupňa. Získané z: Francesphysics.Blog.com.
7. Zill, D. 1984. Algebra a trigonometria. McGraw Hill.