História geometrie pozadia a vývoja z jeho pôvodu

Ten Geometria Začína sa prvými civilizáciami, ktoré využívali túto odvetvie matematiky praktickým spôsobom, konkrétne obyvateľmi Indo Valley a Babylon, ktorí poznali tupé trojuholníky, okolo 3000 až.C.

V spisoch egyptského pisára Ahmesa (1550 až.C.) Metódy sa používajú na výpočet plochy kruhu. Babylončania mali všeobecné pravidlá na meranie objemov a oblastí. 

Ahme papyrus alebo rhind matematický papyrus

Obidve civilizácie, Egypťania aj Babylončania, poznali verzie vety Pythagory 1500 rokov pred pythagorskými verziami. Na druhej strane Indiáni védskeho obdobia (1500-100 až.C.) použitá geometria v konštrukcii oltárov.

[TOC]

Staroveké Grécko

Gréci boli po dlhú dobu naklonení k rozvoju matematiky. Postavy ako Pythagoras a Platón súvisia so všetkými, čo existuje na svete. Matematika bola pre nich kľúčom k interpretácii vesmíru; Tento ideál nasledoval niekoľko storočí v sledovateľoch Pythagorejcov.

Príbehy Miletus

Tales de Mileto bol jedným z prvých Grékov, ktorý prispel k pokroku geometrie. Dlhý čas strávený v Egypte az týchto naučených základných znalostí. Bol prvým, ktorý stanovil vzorce na meranie geometrie.

Príbehy Miletus

Podarilo sa mu zmerať výšku pyramíd Egypta a merať jeho tieň v presnom okamihu, keď sa jeho výška rovnala miere jej tieňa.

Pythagoras

Pythagoras

V rámci najvýznamnejšieho príspevku Pythagory (569 k.C. - 475 a.C.) Do geometrie je slávna veta Pythagorov, ktorá sa uvádza, že v rámci obdĺžnika sa štvorcový pokles (strana na rozdiel od pravého uhla) sa rovná súčtu štvorcov zvyšných strán.

Prvky euklidov

Najvýznamnejšou prácou, ktorá bola zachránená od staroveku, bola štúdia Prvky, z Euclid de Alejandría (325 a.C. - 265 a.C.), vyrobené počas 300. rokov.C. Je to dielo s veľkou historickou hodnotou, ktorá slúži ako základ pre výučbu matematiky už viac ako 2000 rokov.

Euklid

Prvky Bola to jedna z prvých kníh a kompilácií štúdií, ktoré vysvetlili matematické princípy, ktoré by sa dali uplatniť na každú situáciu. Zahŕňa postuláty, ktoré sú základnými zásadami geometrie vo svojej práci. Na druhej strane existujú kvantitatívne princípy známe ako základné pojmy.

Euclid výučba znížila stavebné nástroje v rámci geometrie iba na dve: pravidlo bez opatrení a kompas. To vyvolalo tri klasické problémy, ktoré nenašli odpovede až do devätnásteho storočia: kvadratúra kruhu, duplikácia kocky a trisekcia uhla. 

Môže vám slúžiť: V ktorom storočí Španieli dobyli Tenochtitlán?

Pre staroveku sú dve ideálne geometrické entity priamkou a kruhom, takže väčšina z geometrických teorémov, ktoré boli navrhnuté, boli produktom prieskumu s týmito nástrojmi.

Geometria v astronómii

Geometria bola prospešná aj pre Grékov z hľadiska štúdia hviezd. Vypočítali pohyby pozorovaním a urobili geometrické roviny oblohy, ktoré zakladajú Zem ako ústredný bod, a slnko, ako aj Mesiac a ďalšie planéty a entity, ktoré sa pohybovali okolo nich, a otáčali sa v sade kruhov. 

Jedným z najvplyvnejších príspevkov bol Almagest, napísané v druhom storočí d.C od Claudio Ptolemy (100 D. C.- 170 D.C), astronomická kontajnerka katalógu hviezd. Bol to najkompletnejší text jeho času a ovplyvňoval astronomické štúdie transcendentálnym spôsobom až do stredoveku veľmi pokročilé. Bola to súčasť médií, ktoré najpopulašovali geocentrický systém, ktorý tvrdil, že Zem je centrom vesmíru.

Ptolemicia

Islamský vplyv

V rámci IX storočia, keď bol arabský svet vo svojej veľkej expanzii, veľká časť svojej kultúry prenikla do niekoľkých oblastí vedy a umenia. Boli to veľkí fanúšikovia matematických a filozofických diel Grékov. 

Jednou z najviac preskúmaných vetiev v rámci ich potrieb bola astronómia, aby sa našla presná orientácia, v ktorej mala MECA vykonať vety.

Po štúdiách euklidov a iných príspevkov, ako sú príspevky Ptolemii, moslimovia vyvinuli stereografickú projekciu, to znamená projekciu nebeskej gule v lietadle, aby ju použili ako mapu. To znamenalo pokrok týkajúci sa štúdie trigonometrie.

Medzi najreprezentatívnejšie postavy patrí Thābit Ibn Qurra (826/36-901), ktorý vykonal relevantné preklady starodávnych textov Apollonius, Archimedes, Euclid a Ptolemy. Niektoré z nich sú jedinými prežívajúcimi verziami starodávnych spisov.

Prieskum týkajúce sa astronomickej geometrie tiež umožnilo vytvorenie jedného z najreprezentatívnych nástrojov, Astrolabio, ktoré zjednodušili astronomické výpočty okamihu. Okrem toho im tento nástroj tiež umožnil poznať čas a konečne získať usmernenie na MECA. 

Môže vám slúžiť: 8 zvykov a tradícií Mixtecs

Európsky dedičský rozvoj

V dvanástom storočí, po vložení klasických učení Grékov vďaka moslimskej expanzii a rozvoju ich rovnakých objavov, sa preklady latinských textov priamo z gréčtiny začali robiť priamo z gréčtiny alebo z arabského jazyka. 

To by spôsobilo cestu pre nové vzdelávanie v Európe, ktoré by bolo propagované renesanciou. Znovuobjavenie pojmov, ako napríklad „dôkaz“, začal koncept vyvinutý medzi Grékmi, ktorý sa zaujímal o demonštráciu postulátov v skutočnosti.

Geometria v umení

Znalosti sa odrážali aj v umení, ako je maľovanie alebo architektúra, pretože geometria by sa začala byť základnou súčasťou rozvoja perspektívy v umení.

Filippo Brunelleschi (1377-1446) bol tým, ktorý podarilo rozvíjať lineárnu perspektívu prostredníctvom matematiky. Cieľom tejto teórie bolo reprezentovať v lietadle trojrozmerný priestor z toho, ako ho vnímalo ľudské oko. Týmto sa uvádza, že všetky riadky na obrázku sa museli zbližovať alebo nájsť únik, aby sa vytvoril pocit hĺbky. 

Filippo Brunelleschi. Zdroj: i, Sailko/CC By-S (http: // creativeCommons.Org/licencie/By-SA/3.0/)

Brunelleschi bol prvý, kto opísal perspektívu ako vedecký postup, a to fungovalo ako základ následných pracovných miest v rámci umenia.

V rámci iných príkladov uplatňovania geometrie na štúdium umenia a ľudskej bytosti samo osebe je práca Leonarda da Vinciho (1452 -1519) vo svojom kresbe Muž Vitruvio. Je to štúdia založená na najdokonalejších rozmeroch pre ľudské telo prostredníctvom geometrickej analýzy jeho štruktúry.

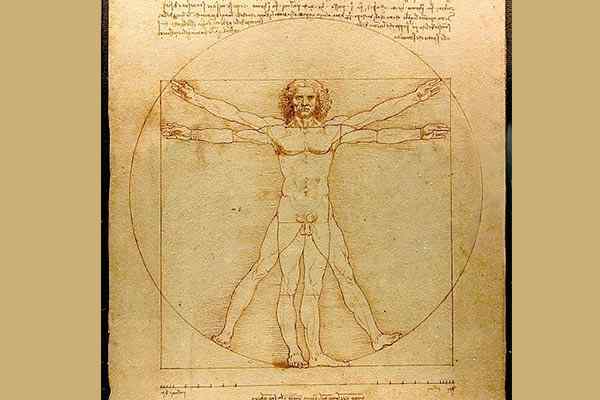Muž Showcase od Leonarda da Vinci / Public Domain

Okrem iných oblastí vyniká aj architektúra, kde sa začali objavovať rôzne prvky ako symetria a rovnováha ako základné vlastnosti. Štvorcové, obdĺžnikové dvere a okná, umiestnené vyváženým spôsobom; Použitie klasických prvkov staroveku, ako sú stĺpce, kupoly a klenby.

Krok k modernosti

Analýza perspektív a projekcií počas renesancie bola jednou z stimulov vzbudenia záujmu matematikov. Od tejto chvíle sa v geometrii začnú zakladať solídnejšie a zložitejšie matematické základne.

Jedným z najdôležitejších diel pre modernitu bolo diela architekta Girarda odzbrojeného (1591-1661), ktoré predpokladalo začiatok projektívnej geometrie. Na jednej strane sa zistilo, že paralelné čiary v projekcii by sa mali zbližovať v bode na nekonečnej čiare, to znamená horizont.

Môže vám slúžiť: Tuxtepec povstanie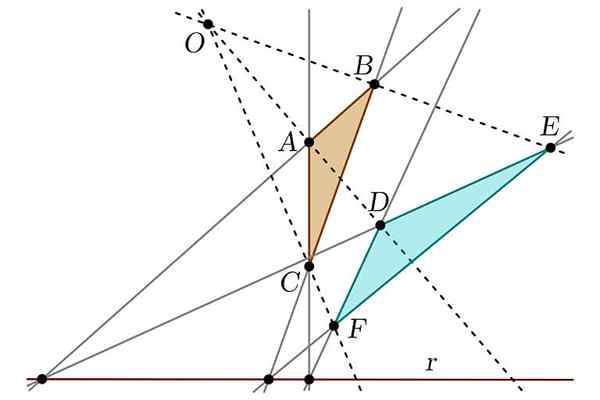Zrušovať vetu

Na druhej strane tiež zistil, čo by sa uznalo ako Disarrangerova veta, ktorá vytvára vzťah medzi dvoma číslami, ktoré možno považovať za „projektívne“. Bol tiež zodpovedný za zjednodušenie diel Apolloniusa s ohľadom na časti kužeľa, čím sa analógie medzi týmto obrázkom a valcom.

Ďalšou veľkou udalosťou tohto obdobia bolo vytvorenie analytickej geometrie prostredníctvom štúdií René Descartes (1596-1650) a Pierre de Fermat (1601-1665) nezávisle. Toto je štúdium geometrie pomocou súradníckeho systému. 

René Descartes pracujú na vašej pracovnej ploche. Wikimedia Commons

Neeuklidovská geometria

Štúdie 18. a 19. storočia sa začali v neuklidovskej geometrii. Konkrétne boli Gauss, Johann Boleai a Lobachevsky, ktorí zistili, že piaty postulat euklid, známy ako paralelný postulát, sa nedal overiť.

Týmto spôsobom vyvinuli typ geometrie, v ktorej bol tento postulát kvalifikovaný ako nepravdivý. Táto nová forma bola úspešná tým, že poskytla uspokojivé výsledky v štýloch geometrie, ktoré nemusia nevyhnutne spĺňať všetky euklidové postuláty. Hyperbolická geometria a eliptická geometria sa teda narodili neskôr.

Je potrebné zdôrazniť prácu Leonharda Eulera (1707-1783) v 18. storočí, pokiaľ ide o rozvoj matematického zápisu. Následne by so sebou dvadsiate storočie prinieslo vývoj špecifickejších oblastí geometrie, medzi ktorými patrí:

-Algebraická geometria: Je to odvetvie matematiky, ktorá kombinuje abstraktnú algebru a analytickú geometriu.

-Konečná geometria: Je to geometrický systém, ktorý sa skladá z konečného množstva bodov, to znamená, že majú koniec alebo limit, a preto sa dajú merať.

-Digitálna geometria: Je to odvetvie informatiky, že štúdium algoritmov a dátových štruktúr, ktoré môžu byť zastúpené geometrický. 

Odkazy

1. (2016) Čo urobilo z euclidových prvkov jedinú knihu, ktorá môže konkurovať Biblii. BBC. BBC sa zotavila.com
2. Tri klasické problémy gréckej matematiky. University of Antioquia. Uzdravené z výučby.vy.Edu.co
3. Heilbron J.L (2020). Geometria. Encyclopædia Britannica. Zotavené z Britannice.com
4. História geometrie. Wikipedia, bezplatná encyklopédia. Získaný z.Wikipedia.orgán
5. Analytická geometria. Wikipedia, bezplatná encyklopédia. Získaný z.Wikipedia.orgán
6. (2017) Geometria a matematika v renesancii. Zotavené z Ukessays.com
7. Sáiz a. Lineárna perspektíva v Brunelleschi. University of Valencia. UV sa získal.je
8. Redaktori Encyclopaedia Britannica (2019). Renesančná architektúra. Encyclopædia Britannica. Zotavené z Britannice.com
9. Andersen K (2020). Girard odzbrojil. Encyclopædia Britannica. Zotavené z Britannice.com
10. (2011) Zaujímavý úvod do výpočtovej geometrie. Zdroj z Gaussians.com