Trigonometrické funkcie a aplikácie jednotného kruhu

On Kruh Je to polomerový kruh rovný 1, ktorý sa zvyčajne zameriava na bod (0,0) karteziánskeho súradnice Xy. Používa sa na ľahké definovanie trigonometrických dôvodov uhlov obdĺžnikami.

Rovnica jednotného kruhu zameraná na pôvod je:

X² + a² = 1

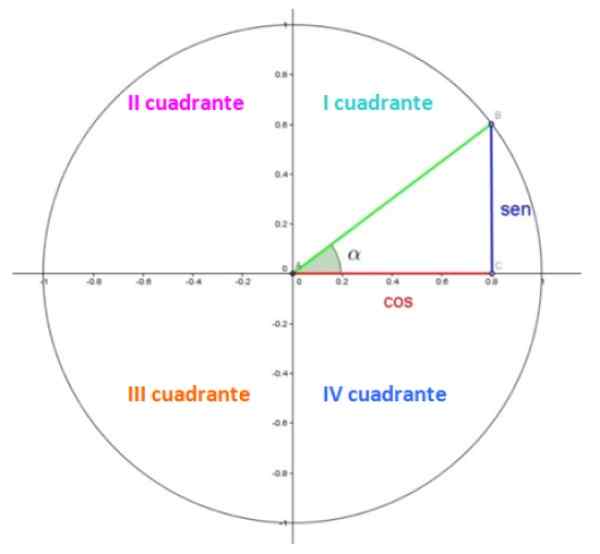
postava 1. Jednotkový kruh. Zdroj: Wikimedia Commons.

Na obrázku 1 máme jednotkový kruh, v ktorom je každá miestnosť v kvadrante. Kvadranty sú očíslované s rímskymi číslami a sú počítané proti horlivosti.

V prvom kvadrante je trojuholník. Kategórie, v červenej a v modrom meraní 0.8 a 0.6, zatiaľ čo hypotenus v zelených opatreniach 1, pretože ide o rádio.

Akútny uhol a je centrálny uhol v štandardnej polohe, čo znamená, že jeho vrchol sa zhoduje s bodom (0,0) a jeho počiatočnou stranou s kladnou osou x. Uhol sa meria v rozpore s hodinovými rukami a na základe konvencie je pridelené pozitívne znamenie.

No, v jednotkovom kruhu sú súradnice coseno a sínus a súradnice X a Y v bode B, ktoré sú v uvedenom príklade 0.8 a 0.6.

Z týchto dvoch sú definované:

• Tg a = sin a/cos α = 0.6/0.8 = 0.75
• Sec a = 1/ cos α = 1/0.8 = 1.25
• poškodenie α = 1 / sin α = 1/0.6 = 1.66 ..
• ctg a = 1/tg = 0.8/0.6 = 1.33 ..

[TOC]

Unitárne kruhové aplikácie

Ak sa obmedzíme na obdĺžniky, trigonometrické dôvody by sa použili iba na akútne uhly. S pomocou jednotkového kruhu sa však výpočet trigonometrických dôvodov rozširuje na akýkoľvek uhol α.

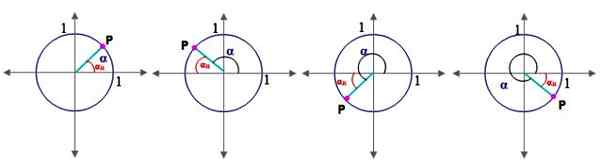Obrázok 2.- Uhly v kvadrantoch a referenčný uhol v jednotkovom kruhu. Zdroj: f. Zapata.

Z tohto dôvodu je potrebné definovať koncept referenčného uhla α ako prvý_R:

Môže vám slúžiť: konečná súprava: Vlastnosti, príklady, vyriešené cvičenia

Referenčný uhol

Nech a je uhol v štandardnej polohe (ten, ktorého Počiatočná strana zhoduje sa s kladnou osou x), jeho referenčný uhol α_R Je medzi jej koncová strana a os x. Obrázok 2 zobrazuje referenčný uhol uhlov v kvadrante I, II, III a IV.

Pre každý kvadrant sa referenčný uhol vypočíta takto:

-Prvý kvadrant: α_R = α

-Druhý kvadrant: α_R = 180 ° - α

-Tretí kvadrant: α_R = α - 180 °

-Štvrtý kvadrant: α_R = 360 ° - α

Všimnite si, že prvý kvadrantový uhol a zhoduje sa s jeho referenčným uhlom. Trigonometrické dôvody uhla a sú rovnaké ako ich referenčný uhol, so znakmi podľa tých, ktorí majú kvadranty, v ktorých je terminálna strana α pádov.

Inými slovami, trigonometrické dôvody Coseno a prsník uhla sa zhodujú s súradnicami bodu P podľa obrázku 2.

Na nasledujúcom obrázku vidíme trigonometrické dôvody niektorých pozoruhodných uhlov, ako je odvodené z jednotkového kruhu.

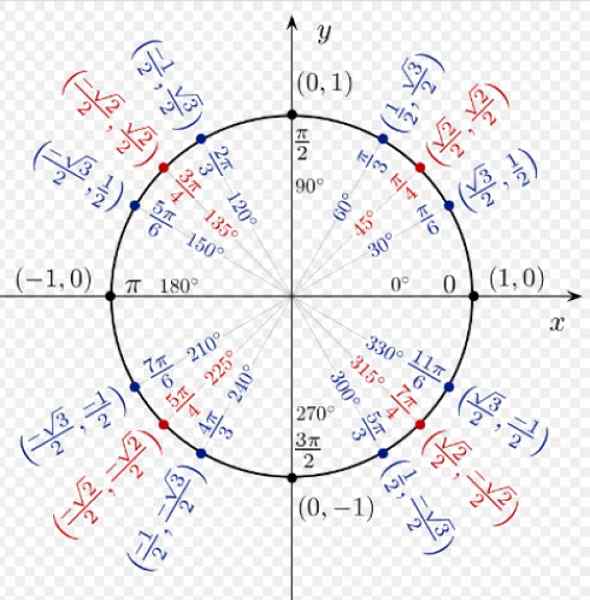Obrázok 3. Súradnice niektorých významných bodov v kruhu jednotky. Zdroj: Wikimedia Commons.

Dôvody, prečo sú coseno a prsia akéhokoľvek uhla v kvadrante I pozitívne. Pre a = 60 ° máme súradnice (1/2; √3/2), ktoré zodpovedajú COS 60 ° a sen 60 °.

Súradnice a = 120 ° sú (-1/2; √3/2), pretože v druhom kvadrante je súradnica x negatívna.

Rozloženie grafov kosínus a sínus

S pomocou jednotkového kruhu a súradnice bodov P na ňom je možné nakresliť grafy funkcií cos t a sen t, ako uvidíme nižšie.

Môže vám slúžiť: uhlové posunutie

Na tento účel je v jednotkovom kruhu umiestnených niekoľko pozícií bodu P (t). Začneme grafom funkcie f (t) = sen t.

Môžeme poznamenať, že keď ideme z t = 0 do t = π/2 (90 °), hodnota sent sa zvyšuje na 1, čo je maximálna hodnota.

Na druhej strane, od t = π/2 do t = 3π/2 hodnota sint T klesá z 1 a prechádza cez 0 pri t = π na svoje minimum -1 pri t = 3π/2.

Obrázok zobrazuje graf prvého cyklu F (t) = sen t, ktorý zodpovedá prvému návratu do kruhu jednotky, táto funkcia je periodická perióda 2π.

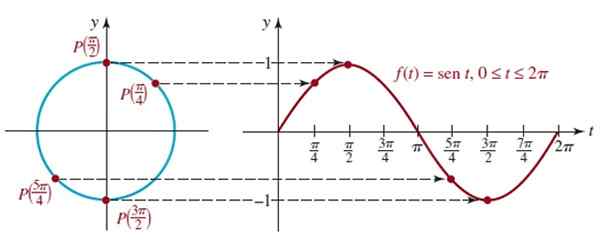Obrázok 4. Obrázok grafu f (t) = sent pre cyklus. Zdroj: Zill, D. Algebra, trigonometria a analytická geometria.

Analogický postup sa môže vykonať, aby sa získal graf funkcie f (t) = cos t, ako je uvedené v nasledujúcej animácii:

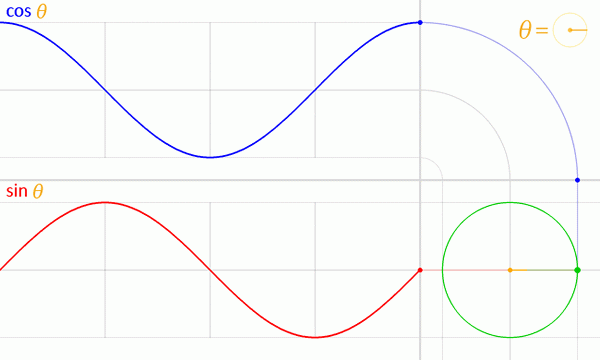Obrázok 5. Grafy sínusu a kosínus funkcie z jednotkového kruhu. Zdroj: Wikimedia Commons.

Vlastnosti Seno a Coseno Funkcie

-Obe funkcie sú kontinuálne v súbore skutočných a tiež periodických čísel, perióda 2π.

-Doména funkcií f (t) = sen t a f (t) = cos t sú všetky skutočné čísla: (-∞, ∞).

-Pre trasu prsníka alebo sínusovej a kosínus máte interval [-1,1]. Zahrnuté sú zátvorky, že -1 a 1 sú zahrnuté.

- Sin t num sú hodnoty, ktoré zodpovedajú nπ celému celému číslu, zatiaľ čo nuly cos t sú [(2n+1)/2] s n tiež celé.

-Funkcia f (t) = sin t je čudná, má symetriu vzhľadom na pôvod, zatiaľ čo funkcia cos t je rovnomerná, jej symetria je vzhľadom na vertikálnu osi.

Môže vám slúžiť: náhodné výbery s výmenou alebo bez výmeny

Vyriešené cvičenia

- Cvičenie 1

Vzhľadom na cos t = - 2/5, čo je horizontálna súradnica bodu P (t) v jednotkovom kruhu v druhom kvadrante, získajte zodpovedajúcu vertikálnu súradnicu Sen t.

Riešenie

Pretože p (t) patrí do jednotkového kruhu, v ktorom sa splní:

X² + a² = 1

Preto:

y = ± √ 1 - x²

Pretože p (t) je v druhom kvadrante, kladná hodnota sa bude brať. Vertikálna súradnica bodu P (t) je y:

y = √ 1 - (-2/5)² = √0.84

- Cvičenie 2

Matematický model teploty Tón V stupňoch Fahrenheita v ktoromkoľvek dni, tón Hodiny po polnoci sú dané:

T (t) = 50 + 10 sen [(π /12) × (t - 8)]

S pochopeným medzi 0 a 24 hodinami. Nájsť:

a) teplota o 8:00.

b) hodiny, počas ktorých t (t) = 60 ° F

c) maximálne a minimálne teploty.

Roztok

V danej funkcii nahradíme t = 8:

T (8) = 50 + 10 sen [(π/12) × (t-8)] = 50 + 10 sen [(π/12) × (8-8)] =

= 50 + 10 x sen 0 = 50 ° F

Riešenie B

50 + 10 sen [(π/12) × (t-8)] = 60

Je to trigonometrická rovnica a vy musíte vyčistiť neznáme „T“:

10 sen [(π/12) × (t -8)] = 60 - 50 = 10

sin [(π/12) × (t-8)] = 1

Vieme, že sen π/2 = 1, preto musí byť argument prsníka 1:

(π/12) × (t-8) = π/2

T-8 = 6

t = 14 h

Dospelo sa k záveru, že 14 hodín po polnoci je teplota 60 °, tj o 14:00. Počas celého dňa (24 hodín) nie je žiadna iná hodina, v ktorej sa to stane.

Riešenie c

Maximálna teplota zodpovedá hodnote, v ktorej Sen [(π/12) × (t-8)] = 1 a je 60 ° F. Na druhej strane, dochádza k minimu, ak Sen [(π/12) × (t -8)] = -1 a je 40 ° F.

Odkazy

1. Figuera, J. 1999. Matematika. 1. Diverzifikovaný. Bolivarian Collegiate Editions.
2. Hoffman, J. Výber matematických problémov. Zväzok 4.
3. Jiménez, r. 2008. Algebra. Sála.
4. Matematika je zábava. Kruh. Získané z: od: Mathsisfun.com.
5. Wikipedia. Identity a vzorce trigonometrie. Obnovené z: je.Wikipedia.orgán.
6. Zill, D. 1984. Algebra a trigonometria. McGraw Hill.