Heptagon

Príklad heptagónu

Čo je heptagon?

On heptagon Je to polygón so siedmimi stranami a siedmimi vnútornými uhlami. Ako geometrické slovo slovo heptagon pochádza z gréčtiny Hepta, čo znamená sedem a gonos, preložené ako uhol. Je to preto polygón so siedmimi uhlami.

Polygón je plochá geometrická postava, ktorá tvorí a zatvára tri alebo viac segmentov, ktoré sa tiež nazývajú strany. Spoločné body, ktoré sa bočné bočné nazývajú Vrcholy.

Oblasť medzi susednými stranami na vnútornej strane obrázku je Vnútorný, ktorého vrchol je tiež jedným z vrcholov heptagónu.

Ak majú všetky strany a vnútorné uhly rovnaké opatrenie, je to pravidelný heptagon, inak je a nepravidelný heptagón. Nepravidelné heptony prijímajú veľké množstvo foriem.

Môže byť tiež heptagón vypuklý ani konkávny, Podľa miery jeho vnútorných uhlov. Ak vnútorné uhly merajú menej ako 180 °, heptagón je konvexný, ale ak jeden alebo viac uvedených uhlov prekročí 180 °, potom je konkávny.

Heptagon, ktorého strany sú rovnaké opatrenie, sa volá Salaterálny. To môže byť konkávne alebo konvexné, pravidelné alebo nepravidelné.

Pravidelný a nepravidelný heptagon

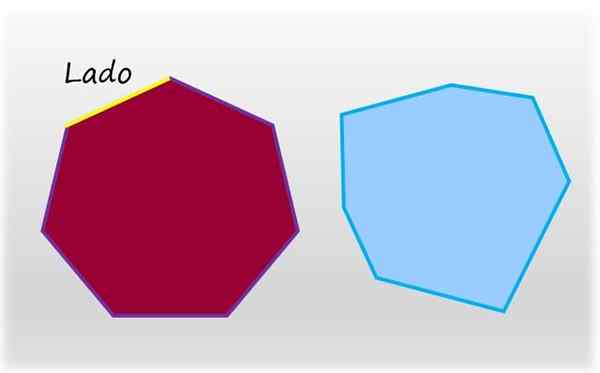Heptagon je plochá a uzavretá postava siedmich strán. Vľavo, pravidelný heptagón, ktorého strany a vnútorné uhly majú rovnakú mieru. Napravo, nepravidelný heptagón. Zdroj: f. Zapata.

Pravidelný heptagón je taký, ktorý má svoje sedem strán a sedem vnútorných uhlov rovnakej miery, opak nepravidelného heptagónu, ktorý má aspoň jednu stranu iného meradla alebo iný vnútorný uhol.

Pravidelný heptagon

Symetria

Pravidelný heptagón je vysoko symetrická postava. Môžu sa nakresliť segmenty, ktoré spájajú vrchol so stredom opačnej strany, z ktorých všetky sa pretína v strede heptagónu. Toto je sedem osí symetrie na obrázku.

Môže vám slúžiť: Oblasť pravidelného a nepravidelného Pentagónu: Ako sa užíva, cvičenia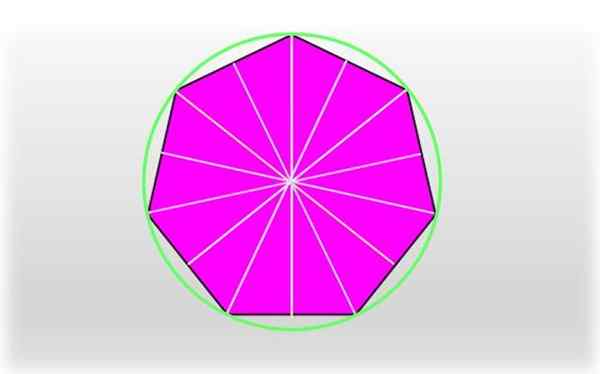 Pravidelný heptagón a jeho symetrické osi. Obvod, ktorý prechádza každým z vrcholov heptagónu.

Segment, ktorý sa spája s vrcholom so stredom heptagónu, sa volá Cirkulódio, Zodpovedá polomeru jedinečného obvodu, ktorý prechádza každým z vrcholov, ako je to znázornené na obrázku.

Uhly

V heptagóne vynikajú nasledujúce uhly:

• Vnútorný ϕ, ktorého vrchol sa zhoduje s jedným z vrcholov heptagónu, keďže sú bokmi uhla, dve susedné strany heptagónu. Pre pravidelný heptagón je miera každého zo siedmich vnútorných uhlov približne 128.57 °.
• Vonkajší uhol, Ten, ktorý sa tvorí medzi jednou zo strán a predĺžením jednej zo susedných strán, je spoločným vrcholom medzi týmito dvoma stranami vrcholu uhla. Podobne sa vytvorí sedem vonkajších uhlov a ich hodnota sa vypočíta odpočítaním 180 ° od vnútorného uhla, ktorý pre pravidelný heptagón vedie k 51.43 °.
• Centrálny uhol θ, Má svoj vrchol v strede pravidelného heptgónu. Vypočíta sa vydelením 360 ° o 7, čo má za následok približne 51.43 °.

Súčet vnútorného uhla a centrálny uhol sa rovná 180 °, to znamená:

ϕ + 9 = π

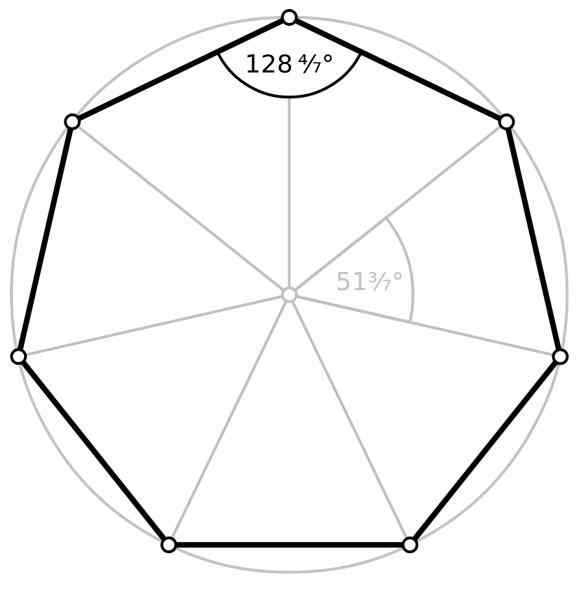Vnútorný uhol a centrálny uhol pravidelného heptagónu. Zdroj: Wikimedia Commons

Oblasť

Pokiaľ ide o pravidelný heptagón, existujú vzorce, zatiaľ čo pre nepravidelný heptagón sa musíte uchýliť k iným metódam, ako je napríklad jeho rozdelenie na iné jednoduchšie polygóny, ako napríklad trojuholníky.

Môže vám slúžiť: Pravidlo T: Charakteristiky, takže je to príklady

Pravidelná plocha heptagonu

1. Ak obvod P a apothém to_p:

Či už do oblasti Heptagon. Existuje vzorec na výpočet oblasti, ktorý je platný pre akýkoľvek pravidelný polygón:

2. Ak sú známe L a apothém do_p:

Pretože obvod je súčet strán a bočné opatrenia L v bežnom heptagóne sa získa:

P = 7 šu

Výmena v predchádzajúcom vzorci:

3. Ak je strana známa        

Nasleduje približný, platný vzorec, keď je známa miera heptagónu:

A = 3.634 ∙ l²

Nepravidelný heptagon

Nepravidelná plocha heptagonu sa dá vypočítať pomocou triagulácia, ktorý spočíva v rozdelení heptagónu na päť trojuholníkov (pozri nasledujúci obrázok). Vypočíta sa plocha každého z nich a výsledky sa pridajú, čím sa získa úplná plocha heptagónu.

Druhá metóda sa volá Determinant, A je potrebné umiestniť heptagón do obdĺžnikového súradnicového systému, aby ste poznali súradnice každého vrcholu. Táto oblasť sa vypočíta vzorcom, ktorý zahŕňa hodnoty týchto súradníc.

Diagonála

Ten diagonála Sú to segmenty, ktoré spájajú vrchol s iným, ktorý nie je nasledujúci (ak segment spojí dva po sebe nasledujúce vrcholy strana). Heptagon má celkovo 14 diagonálov.

Počet diagonálov D ​​ľubovoľného polygónu sa vypočíta prostredníctvom vzorca:

D = n · (n - 3) / 2

Výmena n = 7, zostáva:

D = 7 · (7 - 3) / 2 = 7 · (4/2) = 14

Súčet vnútorných uhlov

Pre akýkoľvek heptagón, bez ohľadu na to, či je pravidelný, súčet jeho vnútorných uhlov sa rovná 900 ° alebo 5π radiánov.

Môže vám slúžiť: trigonometrické dôvody: príklady, cvičenia a aplikácie

Táto vlastnosť je veľmi ľahké demonštrovať, pretože heptagón je rozdelený na jednotlivé trojuholníky, ktoré sa neprekrývajú a kreslia priamočiare segmenty, ktoré spájajú vrcholy, bez toho, aby sa navzájom prekročili.

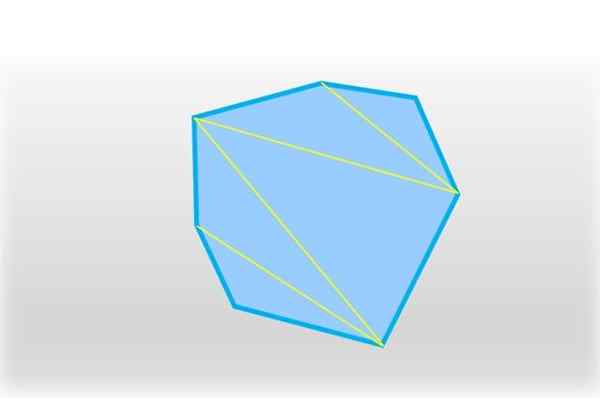Heptagón možno rozdeliť do piatich trojuholníkov, ktoré sa spájajú s segmentom dva, ktoré nekonzkujujú vrcholy. Zdroj: f. Zapata.

Získava sa päť trojuholníkov a v každom z nich je súčet jeho vnútorných uhlov 180 °, čo sa vynásobí 5, ktoré sa rovná 900 °:

5 x 180 ° = 900 °

Vzorce

Obvod

Pre pravidelný heptagón z L sa obvod P vypočíta takto:

P = 7 šu

Ak je obvod nepravidelný, pridajú sa dĺžky každej zo siedmich strán.

Meranie vnútorného uhla

V pravidelnom heptagóne sa vnútorný uhol 9 meria:

9 = [180 (n-2)]/n

Kde n = 7.

Apotém

Buďte na strane pravidelného heptagónu. Apotém je segment, ktorý prechádza zo stredu heptagónu, kolmo na opačnú stranu.

Nechať a_p Dĺžka apotheme. Poznanie polomeru ohraničeného obvodu, ktorý je označený ako r_c A na strane heptagónu, máte:

Poznanie vnútorného uhol 9 je vyššie uvedený ekvivalentný:

Oblasť

Ak je to pravidelný heptagón z L, oblasť A je daná:

A = 3.634 ∙ l²

Keď je heptagón nepravidelný, sú potrebné obdĺžnikové súradnice každého vrcholu (x_n , a_n), Kde n = 1, 2, 3 ... 7.

Potom sa na nájdenie oblasti A použije nasledujúci vzorec:

Diagonála

Počet D diagonálov je uvedený:

D = n · (n - 3) / 2

Kde n = 7 pre heptagon.

Ako vyrobiť heptagon

Nasledujúca animácia ukazuje, ako nakresliť približne pravidelný heptagón, pomocou pravidla a kompasu.

Výstavba pravidelného heptagónu. Zdroj: Wikimedia Commons

Odkazy

1. Alexander, D. 2013. Geometria. 5. Vydanie. Učenie sa.
2. Lemonis, m. Pravidelná kalkulačka hepalle. Obnovené z: CalcResource.com.
3. Matematika otvorená referencia. Polygón. Získané z: Mathpenref.com.
4. Vesmír. Heptagon. Získané z: Universoformulas.com.
5. Wikipedia. Heptagon. Obnovené z: je.Wikipedia.com.