Stupne slobody Ako ich vypočítať, typy, príklady

Ten stupne slobody V štatistike je počet nezávislých zložiek náhodného vektora. Ak má vektor n komponenty a existujú p lineárne rovnice, ktoré súvisia s jeho komponentmi, potom stupeň slobody Je to n-p.

Koncept stupne slobody Objavuje sa tiež v teoretickej mechanike, kde v hrubom režime sú rovnocenné s rozmerom priestoru, kde sa častice pohybujú, s výnimkou počtu ligátov.

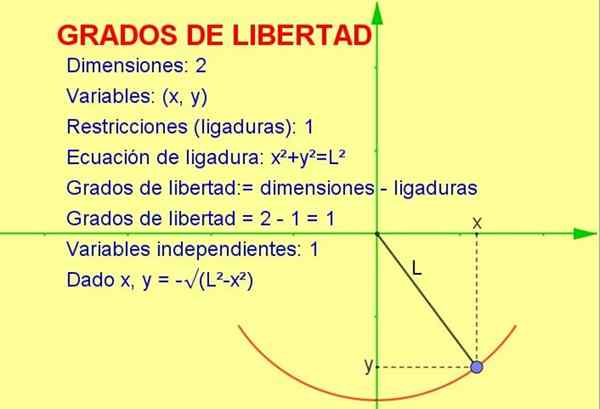
postava 1. Kyvadlo sa pohybuje v dvoch dimenziách, ale má iba určitý stupeň slobody, pretože je povinný pohybovať sa v oblúku polomeru. Zdroj: f. Zapata.

Tento článok bude diskutovať o koncepcii stupňov slobody aplikovanej na štatistiku, ale mechanický príklad sa ľahšie vizualizuje geometricky.

[TOC]

Typy stupňov slobody

Podľa kontextu, v ktorom sa uplatňuje, sa spôsob výpočtu počtu stupňov slobody môže meniť, ale základná myšlienka je vždy rovnaká: celkový rozmer menší počet obmedzení.

V mechanickom prípade

Zoberme si častice, ktorá osciluje zviazanú na lano (kyvadlo), ktoré sa pohybuje vo vertikálnej rovine x-y (2 rozmery). Častica je však povinná pohybovať sa po obvode polomeru rovnajúce sa dĺžke lana.

Pretože častica sa môže pohybovať iba na tejto krivke, počet stupne slobody Je to 1. Toto je možné vizualizovať na obrázku 1.

Spôsob výpočtu počtu stupňov voľnosti je zmeniť počet rozmerov okrem počtu obmedzení:

Stupne voľnosti: = 2 (rozmery) - 1 (ligácia) = 1

Ďalšie vysvetlenie, ktoré nám umožňuje dosiahnuť výsledok, je nasledujúce:

-Vieme, že dve rozmerové polohy sú predstavované súradnicovým bodom (x, y).

-Ale ako tento bod musí splniť rovnicu obvodu (x² + a² = L²) Pre danú hodnotu premennej x, premenná a je určená uvedenou rovnicou alebo obmedzením.

Týmto spôsobom je iba jedna z premenných nezávislá a systém má Jeden (1) stupeň slobody.

Môže vám slúžiť: Klasická pravdepodobnosť: výpočet, príklady, vyriešené cvičenia

V súbore náhodných hodnôt

Na ilustráciu toho, čo tento koncept znamená, predpokladajme vektor

X = (x₁, X₂,…, X_n)

Predstavujúce vzorku n Náhodné hodnoty normálne distribuované. V tomto prípade náhodný vektor X mať n nezávislé komponenty, a preto sa hovorí X mať n stupne slobody.

Postavme teraz vektor r odpad

r = (x₁ - , X₂ - ,.. ., X_n - )

Kde predstavuje priemer vzorky, ktorá sa vypočíta takto:

= (x₁ + X₂ +.. .+ X_n) / n

Potom súčet

(X₁ - )+(x₂ - )+.. .+(X_n - ) = (x₁ + X₂ +.. .+ X_n) - n = 0

Je to rovnica, ktorá predstavuje obmedzenie (alebo ligácia) vo vektorových prvkoch r odpadu, pretože ak sú známe N-1, vektorové komponenty r, Reštrikčná rovnica určuje neznámu zložku.

Preto vektor r dimenzie n s obmedzením:

∑ (x_Jo - ) = 0

Mať (N - 1) stupne slobody.

Opäť sa uplatňuje, že výpočet počtu stupňov voľnosti je:

stupne voľnosti: = n (rozmery) - 1 (obmedzenia) = n -1

Príklady

Rozptyl a stupne slobody

Rozptyl s² Je definovaný ako priemer štvorca odchýlok (alebo odpadu) vzorky údajov:

siež² = (r•r) / (N-1)

kde r je vektor odpadu r = (x1 -, x2 -, .. ., Xn -) a hrubý bod (•) je skalárny operátor produktu. Prípadne je možné vzorec rozptylu napísať takto:

siež² = ∑ (x_Jo - )² / (N-1)

V každom prípade by sa malo poznamenať, že pri výpočte priemeru štvorca odpadu je rozdelený (n-1) a nie medzi n, pretože ako je uvedené v predchádzajúcej časti, počet stupňov slobody voľnosti vektor r je (n-1).

Ak pre výpočet rozptylu bol rozdelený medzi n Namiesto (n-1) by výsledok mal zaujatosť, ktorá je veľmi významná pre hodnoty n Menej ako 50.

Môže vám slúžiť: analytická geometria

V literatúre sa tiež javí ako vzorec rozptylu s deliteľom N namiesto (N-1), pokiaľ ide o rozptyl populácie.

Ale sada náhodnej premennej odpadu, reprezentovaná vektorom r, Aj keď má rozmer N, má iba (N-1) stupne voľnosti. Ak je však číslo údajov dostatočne veľké (n> 500), obe vzorce sa konvertujú na rovnaký výsledok.

Kalkulačky a tabuľky ponúkajú dve verzie rozptylu a štandardnú odchýlku (ktorá je odmocninou rozptylu).

Naše odporúčanie, vzhľadom na tu uvedenú analýzu, je vždy zvoliť verziu s (n-1) zakaždým, keď je potrebné vypočítať rozptyl alebo štandardnú odchýlku, aby ste sa vyhli výsledkom so zaujatosťou.

V štvorcovej distribúcii Chi

Niektoré rozdelenie pravdepodobnosti v kontinuálnej náhodnej premennej závisí od parametra s názvom stupeň slobody, Toto je prípad distribúcie štvorcových štvorcov (χ²).

Názov uvedeného parametra pochádza práve z stupňov slobody náhodného vektora, na ktorom je tento distribúcia aplikovaný.

Predpokladajme, že existujú populácie G, z ktorých sú odobraté vzorky veľkosti n:

X₁ = (x1₁, x1₂,... x1_n)

X2 = (x2₁, x2₂,... x2_n)

.. .

X_J = (xj₁, xj₂,… Xj_n)

.. .

Xg = (xg₁, Xg₂,… Xg_n)

Obyvateľstvo J To má priemernú a štandardnú odchýlku SJ, Postupujte podľa normálnej distribúcie n (, SJ ).

Typifikovaná alebo normalizovaná premenná ZJ_Jo je definovaný ako:

Zj_Jo = (xj_Jo - ) / SJ.

A vektor Zj Je to definované takto:

Zj = (Zj₁, Zj₂,..., zj_Jo,..., zj_n) A postupujte podľa normálneho distribúcie typizovaného n (0,1).

Potom premenná:

Otázka = ((Z1₁ ^2 + z2₁^2+… . + Zg₁^2),… ., (Z1_n^2 + z2_n^2+… . + Zg_n^2))

Postupujte podľa distribúcie χ²g) nazývané Distribúcia Chi Square s stupňom slobody g.

V kontraste s hypotézou (s rozlíšeným príkladom)

Ak chcete urobiť kontrast hypotézy na základe určitej sady náhodných údajov, je potrebné poznať Počet stupňov slobody g Aby ste mohli použiť test Chi Square Test.

Môže vám slúžiť: Kontinuálne rovnomerné rozdelenie: charakteristiky, príklady, aplikácie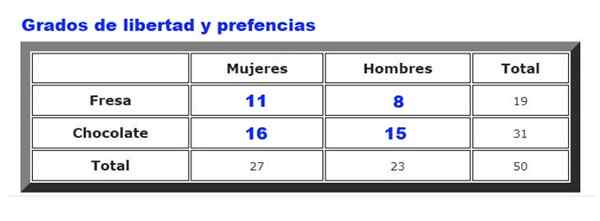 Obrázok 2. Existuje vzťah medzi zmrzlinou a pohlavím zákazníkov? Zdroj: f. Zapata.

Napríklad údaje zozbierané na preferenciách čokolády alebo jahody medzi mužmi a ženami v nejakom obchode so zmrzlinou sa budú analyzovať. Frekvencia, s akou si muži a ženy vyberajú jahody alebo čokoládu, je zhrnutá na obrázku 2.

Po prvé, vypočíta sa očakávaná tabuľka frekvencie, ktorá sa vytvára vynásobením Celkové riadky pre neho Celkové stĺpce, deleno Celkové údaje. Výsledok je znázornený na nasledujúcom obrázku:

Obrázok 3. Výpočet očakávaných frekvencií na základe pozorovaných frekvencií (modré hodnoty na obrázku 2). Zdroj: f. Zapata.

Potom pokračujeme v výpočte štvorca Chi (z údajov) podľa nasledujúceho vzorca:

hrebeň² = ∑ (f_ani - F_a)² / F_a

Kde f_ani sú pozorované frekvencie (obrázok 2) a f_a sú očakávané frekvencie (obrázok 3). Suma je nad všetkými radmi a stĺpcami, ktoré v našom príklade uvádzajú štyri výrazy.

Po vykonaní operácií dostanete:

hrebeň² = 0,2043.

Teraz je potrebné porovnávať s teoretickým štvorcom, ktorý závisí od Počet stupňov slobody g.

V našom prípade je toto číslo určené nasledovne:

G = (#Filas - 1) (#columnas - 1) = (2 - 1) (2 - 1) = 1 * 1 = 1.

Ukazuje sa, že počet stupňov slobody g tohto príkladu je 1.

Ak chcete overiť alebo odmietnuť nulovú hypotézu (H0: Neexistuje žiadna korelácia medzi chuťou a pohlavím) s úrovňou významnosti 1%, teoretický štvorec chi sa počíta s stupňom slobody G = 1.

Vyžaduje sa hodnota, ktorá vytvára akumulovanú frekvenciu (1 - 0.01) = 0.99, to je 99%. Táto hodnota (ktorá sa dá získať z tabuliek) je 6.636.

Keď teoretický chi prekoná vypočítaný, potom sa overuje nulová hypotéza.

To znamená, že so zozbieranými údajmi neexistuje žiadny vzťah medzi príchuťou premenných a pohlavím.

Odkazy

1. Minitab. Aké sú stupne slobody? Zdroj: Podpora.Minitab.com.
2. Moore, David. (2009) Základné aplikované štatistiky. Editor Antoni Bosch.
3. Leigh, Jennifer. Ako vypočítať stupne slobody v štatistických modeloch. Získané z: Geniolandia.com
4. Wikipedia. Stupeň slobody (štatistika). Obnovené z: je.Wikipedia.com
5. Wikipedia. Stupeň slobody (fyzické). Obnovené z: je.Wikipedia.com