Stupeň polynómu, ako sa určuje, príklady a cvičenia

On stupeň polynómu v a premenná je daná pojmom, ktorý má hlavný exponent, a ak má polynóm dve alebo viac premenných, Potom je stupeň určený súčtom exponentov každého termínu, pričom hlavnou súčtom polynómu je.

Pozrime sa, ako určiť stupeň polynómu praktickým spôsobom.

postava 1. Slávna Einsteinova rovnica pre energiu E je absolútnym monomiálnym menom 1. pre hmotnostnú premennú označenú M, pretože rýchlosť svetla C sa považuje za konštantnú. Zdroj: piqsels.

Predpokladajme, že polynóm P (x) = -5x + 8x³ + 7 - 4x². Tento polynóm má premennú, v tomto prípade je to premenná X. Tento polynóm pozostáva z niekoľkých výrazov, ktoré sú nasledujúce:

-5x; 8x³; 7; - 4x²

 Vyberme si zo štyroch výrazov, ktorých exponent je väčší, tento výraz je:

8x³

A teraz, čo je exponent? Odpoveď je 3. Preto P (x) je polynóm stupňa 3.

Ak má príslušná polynóm viac ako jedna premenná, potom môže byť tento stupeň:

-Absolútny

-Vo vzťahu k premennej

Absolútny titul je vysvetlený na začiatku: pridanie exponentov každého pojmu a výber najväčšieho.

Na druhej strane, stupeň polynómu vzhľadom na jednu z premenných alebo písmen, je najväčšou hodnotou exponentu, ktorý uviedol písmeno. Bod bude jasnejší s príkladmi a cvičeniami vyriešenými z nasledujúcich častí.

[TOC]

Príklady známky polynómu

Polynomiály sa dajú klasifikovať podľa titulu, ktoré sú schopné mať prvý stupeň, druhý stupeň, tretí stupeň atď. Pre príklad na obrázku 1 je energia prvou monomiálnou hmotnosťou.

Môže vám slúžiť: Zhoda: zhodné čísla, kritériá, príklady, cvičenia

Je tiež dôležité poznamenať, že počet výrazov, ktoré má polynóm, sa rovná stupňu plus 1. Tak:

-Polynomiály prvého stupňa majú 2 výrazy: a₁x + a_ani

-Druhý polynóm s degom má 3 výrazy: a₂X² + do₁x + a_ani

-Polynóm tretieho stupňa má 4 výrazy: a₃X³ + do₂X² + do₁x + a_ani

A tak ďalej. Pozorný čitateľ bude pozorovať, že polynómy predchádzajúcich príkladov sú napísané klesajúcim spôsobom, to znamená najprv umiestnenie pojmu s hlavným stupňom.

V nasledujúcej tabuľke sa objavujú rôzne polynómy, a to z jednej aj niekoľkých premenných a ich príslušných absolútnych stupňov:

stôl 1. Príklady polynómov a ich stupňov

Polynóm	Stupeň
3x4+5x3-2x+3	4
7x3-2x2+3x-6	3
6	0
X-1	1
X5-BX4+ABX3+AB3X2	6
3x3a5 + 5x2a4 - 7xy2 + 6	8

Posledné dva polynómy majú viac ako jednu premennú. Termín, ktorý má najväčší absolútny titul, vynikal tučným písmom, takže čitateľ rýchlo skontroluje titul. Je dôležité si uvedomiť, že keď premenná nemá písomný exponent, chápe, že uvedený exponent sa rovná 1.

Napríklad v významnom termíne AB³X² Existujú tri premenné, konkrétne: do, b a X. V tomto termíne, do Je zvýšená na 1, to znamená:

a = a¹

Preto AB³X² = a¹b³X²

Pretože exponent B je 3 a x je 2, okamžite sa dodržiava, že stupeň tohto termínu je:

1+3+2 = 6

A je to absolútny stupeň polynómu, pretože žiadne iné z týchto výrazov nemá väčší stupeň.

Postup pri práci s polynómami

Pri práci s polynómami je dôležité venovať pozornosť tomuto stupňu, pretože v prvom rade a pred vykonaním akejkoľvek operácie je vhodné postupovať podľa týchto krokov, na ktoré tento stupeň poskytuje veľmi dôležité informácie:

-Objednajte si preferenčný polynóm v klesajúcom zmysle. Týmto spôsobom je termín s najvyššou známkou vľavo a ten s najnižším vpravo.

Môže vám slúžiť: endacegon

-Znížte podobné výrazy, postup, ktorý spočíva v pridávaní všetkých podmienok rovnakej premennej a stupňa, ktoré sú vo výraze algebraicky expresie.

-Ak je to potrebné, polynómy sú dokončené a rozptýlia sa výrazmi, ktorých koeficient je 0, v prípade podmienok s určitým exponentom.

Objednať, znížiť a dokončiť polynóm

Vzhľadom na polynóm P (x) = 6x² - 5x⁴- 2x+3x+7+2x⁵  - 3x³ + X⁷ -12 Vyžaduje sa, aby sa nariadil, aby sa znížil, znížil podobné podmienky, ak existujú a dokončite podmienky, ktoré chýbajú v presnosti.

Prvá vec, ktorú treba hľadať, je termín s hlavným exponentom, ktorý je stupňom polynómu, ktorý sa ukáže ako:

X⁷

Preto P (x) je stupeň 7. Potom je nariadený polynóm, počnúc týmto výrazom vľavo:

P (x) = x⁷ + 2x⁵ - 5x⁴ - 3x³ + 6x² - 2x+3x+7 -12

Podobné výrazy sú teraz znížené, ktoré sú nasledujúce: - 2x a 3x na jednej strane. A 7 a -12 na druhej strane. Aby sa ich znížilo, koeficienty sa pridávajú algebraicky a premenná sa ponechá nezmenená (ak sa premenná neobjaví vedľa koeficientu, treba pamätať na to, že x⁰ = 1):

-2x+3x = x

7 -12 = -5

Tieto výsledky sa nahradia v p (x):

P (x) = x⁷ +2x⁵ - 5x⁴ - 3x³ + 6x² + x -5

A nakoniec sa polynóm skúma, aby sa zistilo, či chýba exponent a v skutočnosti, termín, ktorého exponent je 6, chýba, preto je dokončený s nulami, ako je tento:

P (x) = x⁷ + 0x⁶ +2x⁵ - 5x⁴ - 3x³ + 6x² + X - 5

Teraz sa zistilo, že polynóm bol ponechaný s 8 termínmi, pretože, ako už bolo povedané, počet výrazov sa rovná stupňu + 1.

Dôležitosť stupňa polynómu v súde a odčítaní

Pri polynómoch je možné vykonať súčet a odčítanie operácií, v ktorých sa pridávajú alebo odpočítajú iba podobné výrazy, ktoré sú rovnakou premennou a rovnakým stupňom. Ak neexistujú žiadne podobné výrazy, súčet alebo odčítanie zostanú jednoducho uvedené.

Môže vám slúžiť: distribučný majetok

Po vykonaní súčtu alebo odčítania, ktoré sú súčtom opaku, je stupeň výsledného polynómu vždy rovný alebo menší ako stupeň polynómu vo väčšom stupni.

Vyriešené cvičenia

- Cvičenie vyriešené 1

Nájdite nasledujúcu sumu a určte jeho absolútny stupeň:

do³- 8ax²  + X³ + 5²X - 6ax² - X³ + Tretí³ - 5²x - x³ + do³+ 14ax² - X³

Riešenie

Je to polynóm dvoch premenných, takže je vhodné znížiť podobné výrazy:

do³- 8ax²  + X³ + 5²X - 6ax² - X³ + Tretí³ - 5²x - x³ + do³+ 14ax² - X³ =

= a³ + Tretí³ + do³ - 8ax² - 6ax²+ 14ax² +5²X - 5a²x+ x³- X³- X³- X³ =

= 5a³ - 2x³

Oba výrazy sú v každej premennej stupni 3. Preto absolútny stupeň polynómu je 3.

- Cvičenie vyriešené 2

Vyjadriť ako polynóm oblasť nasledujúceho plochého geometrického obrázku (obrázok 2 vľavo). Aký je výsledný stupeň polynómu?

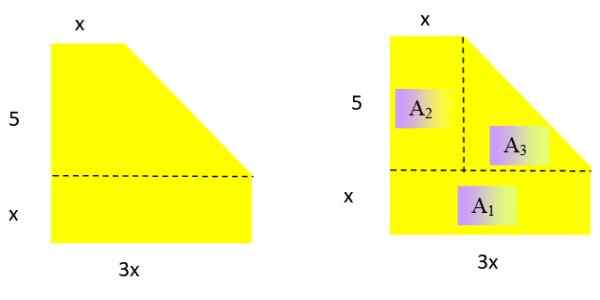Obrázok 2. Vľavo, číslo za rok vyriešené 2 a vpravo, rovnaké číslo sa rozložilo v troch oblastiach, ktorých výraz je známy. Zdroj: f. Zapata.

Riešenie

Výsledný polynóm, ktorý je v oblasti, musí byť stupňom 2 v premennej x. Na určenie primeraného výrazu pre oblasť je číslo rozdelené do známych oblastí:

Oblasť obdĺžnika a trojuholníka sú: Výška a Base X Výška /2

Do₁ = x . 3x = 3x²; Do₂ = 5 . x = 5x; Do₃ = 5 . (2x /2) = 5x

Poznámka: Základ trojuholníka je 3x - x = 2x a jeho výška je 5.

Teraz sa pridávajú tri získané výrazy, s tým máte plochu obrázku v závislosti od toho X:

3x² + 5x + 5x = 3x² + 10x

Odkazy

1. Baldor, a. 1974. Elementárna algebra. Venezuelský kultúrny.Do.
2. Jiménez, r. 2008. Algebra. Sála.
3. Wikilibros. Polynómia. Obnovené z: je. Wikibooks.orgán.
4. Wikipedia. Stupeň (polynóm). Obnovené z: je.Wikipedia.orgán.
5. Zill, D. 1984. Algebra a trigonometria. Mac Graw Hill.