Matematika

Vektorové funkcie

4501
1467
Alfréd Blaho

Čo sú vektorové funkcie?

A vektorová funkcia parameter tón, Je to funkcia, ktorej doména sú skutočné hodnoty tón, zatiaľ čo trasa tvorí vektory formulára r (tón). Takáto funkcia možno vyjadriť ako:

r (tón) = f (tón) Jo + g (tón) J + H (tón) klimatizovať

Kde Jo, J a klimatizovať Sú jednotkové vektory v troch hlavných smeroch priestoru a funkcie f, g a h sú skutočnými funkciami premennej tón. Zápis využíva tučný čas na rozlíšenie vektorových veľkostí.

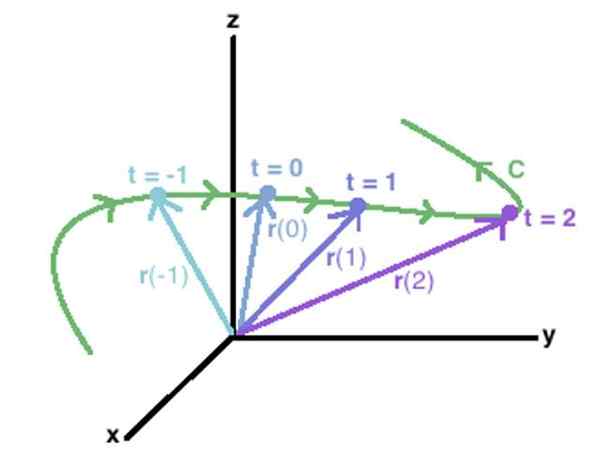Na opis krivky C sa môže použiť vektorová funkcia vo vesmíre, ktorá spája extrémne body každého z vektorov určených uvedenou funkciou. Zdroj: Wikidot.

Ďalším spôsobom, ako označiť vektorovú funkciu, je cez štvorcové zátvorky:

r (tón) = tón), G (tón), H (tón)>

Vektorové funkcie sa môžu použiť na štúdium kriviek v rovine a priestore, ako je napríklad trajektória, ktorá sleduje pohybujúci sa objekt. Príkladom je podobenstvo opísané premietanou loptou s počiatočnou rýchlosťou, pod gravitáciou.

Ak chcete poznať polohu lopty v každom okamihu tón, Vektorová funkcia s dvoma komponentmi, jedna vodorovná a jedna vertikálna:

r (tón) = x (tón) Jo + a (tón) J

Obidve x (tón) ako y (tón) Sú časové funkcie tón. Preto pri vstupe do extrémnych bodov každého z vektorov r(tón) Možné, vytvorte podobenstvo opísané loptou v rovine Xy.

Koncept sa ľahko rozširuje na krivku C vo vesmíre, ako je tá, ktorá je znázornená na obrázku vyššie. V ňom sa objavujú vektory r (-1), r (0), r (1) r (2), ktorého konce kreslia krivku C, nakreslené zelenou farbou.

Limity, odvodené a neoddeliteľné vektorové funkcie

Výpočtové nástroje, ktoré sa vzťahujú na skutočné reálne premenné funkcie, sa dajú použiť aj na vektorové funkcie.

Môže vám slúžiť: faktorizácia

Limit vektorovej funkcie

Limit vektorovej funkcie r (tón) = f (tón) Jo + g (tón) J + H (tón) klimatizovať, Keď t → a, je definovaný ako:

$\dpi110 \displaystyle \lim_t \to a\textbfr(t)=\left [ \displaystyle \lim_ t\to a f(t)\right ]\textbfi+\left [ \displaystyle \lim_ t\to a g(t)\right ]\textbfj+\left [ \displaystyle \lim_ t\to a h(t)\right ]\textbfk$

Za predpokladu, že existujú príslušné limity f (tón), G (tón) a h (tón), kedy tón → a.

Odvodené z vektorovej funkcie

Definícia odvodená z vektorovej funkcie r (t) = f (tón) Jo + g (tón) J + H (tón) klimatizovať Je to analogické s derivátom skutočnej funkcie skutočnej premennej. Volanie r'(t) na uvedenom deriváte, máte:

$\dpi110 \mathbfr'(t)=\displaystyle \lim_\Delta t \to 0\frac\mathbfr(t+\Delta t)-\mathbfr(t)\Delta t$

Derivát existuje vždy, keď existuje predchádzajúci limit, a ak áno, funkcia r(tón) je diferencovateľné v tón.

Integrál vektorovej funkcie

Byť r (t) = f (tón) Jo + g (tón) J + H (tón) klimatizovať vektorová funkcia, takže funguje F, G a H, sú integrovateľné v tón.

Tak:

$\dpi110 \int \mathbfr(t)dt =\left [ \int f(t)dt \right ]\mathbfi+\left [ \int g(t)dt \right ]\mathbfj+\left [ \int h(t)dt \right ]\mathbfk+\mathbfC$

C = c₁Jo + c₂J

Čo znamená, že integračná konštanta je tiež vektor, ale konštantná.

Príklady vektorovej funkcie

Príklad 1

Máte vektorovú funkciu daná pomocou r (tón) = 3 s tón Jo + 2tan tón J. Je možné ho vyhodnotiť pre rôzne hodnoty t, ako napríklad t = π/4 a t = π, čo vedie k vektorom r (π/4) a r (π):

r (π/4) = 3 s (π/4) Jo + 2tan (π/4) J = 3√2 Jo + 2 J

r (π) = 3 s (π) Jo+2tan (π) J = - 3 Jo

Však, r (tón) Neexistuje pre hodnoty t = ∓π/2, ∓3π/2, ∓5π/2…, od funkcie SEC tón = 1 /cos tón Nie je definovaný, je to tak tón = Sen tón / cos tón.

Preto je doménou funkcie R (T) všetky skutočné hodnoty T, s výnimkou hodnoty formulára:

∓ (2n+1) π/2; S n = 0, 1, 2, .. .

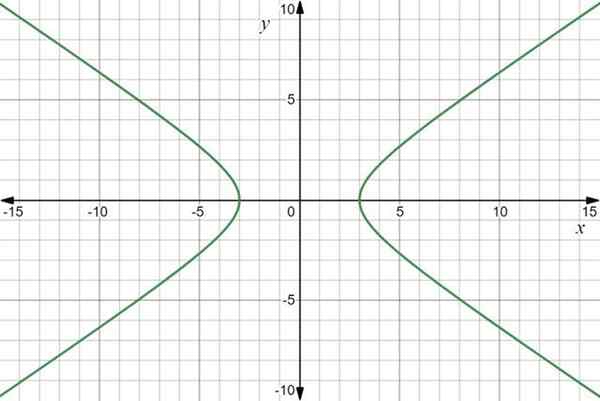
Graf funkcie je hyperbola:

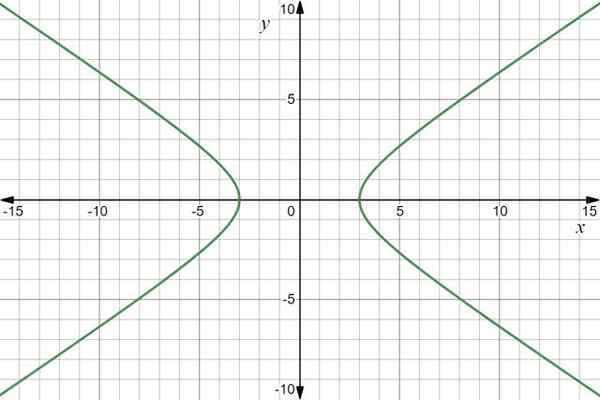Graf funkcie vektora r (t) = 3sec t Jo+2 tan t J. Zdroj: f. Zapata cez Desmos.

Príklad 2

Pri sklone spustenia projektilu je mobilná pozícia vektorová funkcia r (tón) = x (tón) Jo + a (tón) J . Za predpokladu, že odpor vzduchu nezasahuje a že gravitácia je jedinou silou, ktorá pôsobí na mobil, horizontálny pohyb je rovnomerný priamy, zatiaľ čo vertikál je rovnomerne zrýchlený, pretože G = 9.8 m/s² Hodnota zrýchlenia. Toto zrýchlenie je vertikálne smerom k zemi.

Môže vám slúžiť: pravidlá odvodenia (s príkladmi)

V tomto prípade funkcie x (tón) a (tón) Sú to:

x (t) = x_ani + vložka_vôl∙ t
a (t) = y_ani + vložka_Odvoz∙ t - ½ gt²

Sumy v_vôl a v_Odvoz Sú to komponenty vektorovej funkcie, ktoré vždy popisujú mobilnú rýchlosť:

vložka (tón) = v_X(tón) Jo + vložka_a(tón) J

vložka_vôl = v_ani∙ cos θ
vložka_Odvoz = v_ani∙ sen θ

Byť 9 uhol, ktorý tvorí počiatočnú rýchlosť vzhľadom na vodorovnú.

Pokiaľ ide o svoju časť, počiatočnou polohou mobilu je súradnicový bod (x_ani,a_ani) alebo rovnocenne, polohový vektor daný:

r_ani (tón) = x_ani Jo + a_ani J

Všimnite si, že v zobrazených rovniciach bol negatívny znak priradený vertikálnemu smeru, takže tretí termín rovnice pre y (t) ju berie. Je tiež možné priradiť pôvod k počiatočnej polohe mobilu.

Okamžitá rýchlosť projektilu

Okamžitá rýchlosť V (t) je prvá odvodená z polohy, vzhľadom na čas. Vypočíta sa uplatňovaním známych pravidiel derivácie:

vložka(t) = R ' (tón) = [x (tón) Jo + a (tón) J]'= X '(tón) Jo + a '(tón) J = vložka_vôlJo + (v_Odvoz - Gt) J

Rýchlostný modul je daný:

$\dpi110 \left|\textbfv \right|=\sqrtv_ox^2+v_oy^2$

Okamžité zrýchlenie projektilu

Je známe, že je to G, vo vertikálnom smere a smerovaní nadol. Toto je overené s vedomím, že zrýchlenie je prvým derivátom rýchlosti vzhľadom na čas (alebo druhý derivát polohy vzhľadom na čas, ak sa uprednostňuje):

do(t) = V ' (tón) = [V_vôlJo + (v_Odvoz - Gt) J] '= [V_vôlJo] '+ [(v_Odvoz - Gt) J] '= = - g J

Toto je presne očakávaný výsledok.

Cvičenie

Vzhľadom na vektorovú funkciu r (tón) = 3T Jo + (T - 1) J, Nájsť R '(t) a r "(T).

Riešenie

Uplatňovanie pravidiel derivácie na každú z komponentov máte:

Môže vám slúžiť: integrácia konštanta: význam, výpočet a príklady

R '(t) = = 3 Jo + J

A pretože derivát konštanty je 0:

r "(t) = 0

To znamená, r "(t) sa rovná nulovému vektoru.

Odkazy

Figueroa, D. 2005. Séria: Fyzika pre vedu a inžinierstvo. Zväzok 1. Kinematika. Editoval Douglas Figueroa (USB).
Larson, R. Výpočet analytickou geometriou. Druhý. Vydanie. McGraw Hill.
Matematika. Funkcie s hodnotou vektorov. Obnovené z: Mathonline.Wikidot.com.
Opentax. Počet objem 3. Zdroj: Openstax.orgán.
Purcell, e. J. 2007. Kalkulácia. Pearson Vzdelanie.