Typy transcendentných funkcií, definícia, vlastnosti, príklady

Ten transcendentné funkcie Elemental sú exponenciálne, logaritmické, trigonometrické, inverzné trigonometrické funkcie, hyperbolické a inverzné hyperbolické. To znamená, že sú to tie, ktoré nemôžu byť vyjadrené polynómom, polynómovým alebo polynómovým koreňom. 

Non-elementárne transcendentné funkcie sú známe aj ako špeciálne funkcie a medzi nimi môže byť chybová funkcia pomenovaná. Ten algebraické funkcie (polynómy, polynómové kvocienty a polynomické korene) vedľa transcendentné funkcie Elementals predstavuje to, čo je v matematike známe ako elementárne funkcie.

Považuje sa tiež za transcendentné funkcie, ktoré sú výsledkom operácií medzi transcendentnými funkciami alebo medzi transcendentnými a algebraickými funkciami. Tieto operácie sú: súčet a rozdiel funkcií, produktu a pomer funkcií, ako aj zloženie dvoch alebo viacerých funkcií.

[TOC]

Definícia a vlastnosti

Exponenciálna funkcia

Je to skutočná funkcia skutočnej nezávislej premennej formulára:

f (x) = a^x = a^X

kde do Je to pozitívne skutočné číslo (A> 0) fixované nazývané základňa. Circumflejo alebo dohľad sa používajú na označenie potenciálnej operácie.

Poďme pre prípad A = 2 Potom je funkcia taká:

f (x) = 2^x = 2^X

Ktoré sa vyhodnotia pre niekoľko hodnôt nezávislej premennej X:

Nižšie je grafika, kde je reprezentovaná exponenciálna funkcia pre niekoľko základných hodnôt vrátane základne a (Neper číslo a ≃ 2.72). Základňa a Je také dôležité, že vo všeobecnosti, keď hovoríte o exponenciálnej funkcii, premýšľate E^x, to sa tiež označuje exp (x).

postava 1. Exponenciálna funkcia a^x, pre niekoľko hodnôt základne a. (Vlastné rozpracovanie)

Vlastnosti exponenciálnej funkcie

Z obrázku 1 je zrejmé, že doména exponenciálnych funkcií sú reálne čísla (DOM F = R) a rozsah alebo trasa sú pozitívne skutočné (Ran f = R⁺). 

Môže vám slúžiť: symetria

Na druhej strane, bez ohľadu na hodnotu základne A, všetky exponenciálne funkcie prechádzajú bodom (0, 1) a podľa bodu (1, a). 

Keď základňa A> 1, Potom funkcia rastie a kedy 0 < a < 1 Funkcia klesá. 

Krivky y = a^x a y = (1/a)^x  Sú symetrické vzhľadom na os A. 

S výnimkou prípadu A = 1, Exponenciálna funkcia je injekčná, tj k každej hodnote obrázka, zodpovedá a iba počiatočná hodnota.

Logaritmická funkcia

Je to skutočná funkcia skutočnej nezávislej premennej na základe definície logaritmu čísla. Založený na logaritme do číslo X, Je to číslo a na ktorý musí byť základňa zvýšená, aby sa získal argument X:

protokol_do(x) = y ⇔ a^y = x

To znamená, funkcia logaritmu v základni do Je to inverzná funkcia na exponenciálnu funkciu založenú na do.

Napríklad:

protokol₂1 = 0, pretože 2^0 = 1

Ďalší prípad, denník₂4 = 2, pretože 2^2 = 4

Koreňový logaritmus 2 je log₂√2 = ½, pretože 2^½ = √2

protokol₂ ¼ = -2, v pohľade, že 2^(-2) = ¼ 

Nižšie je graf funkcie logaritmu v rôznych základoch.

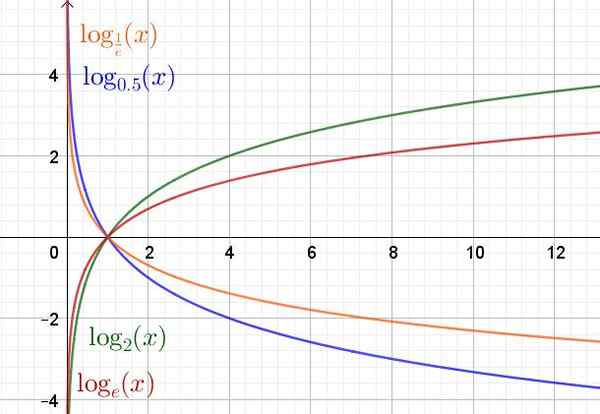Obrázok 2. Exponenciálna funkcia pre rôzne základné hodnoty. (Vlastné rozpracovanie)

Vlastnosti funkcie logaritmo

Doména funkcie logaritmu a (x) = logdo(X)  Sú to pozitívne reálne čísla R+. Rozsah alebo trasa sú skutočné čísla R.

Bez ohľadu na základňu funkcia logaritmu vždy prechádza bodom (1.0) a bod (a, 1) patrí do grafu uvedenej funkcie.

Môže vám slúžiť: Teória frontov: História, model, pre čo je pre to a príklady pre

V prípade, že základňa A je väčšia ako jednotka (a> 1) funkcia logaritmu sa zvyšuje. Ale áno (0 < a < 1) entonces es una función decreciente.

Funkcie Seno, Coseno a Tangent

Funkcia sínusu priraďuje skutočné číslo a každej hodnote x, kde x predstavuje mieru uhla v Radianoch. Na získanie hodnoty Sen (x) z uhla je uhol reprezentovaný v jednotkovom kruhu a projekcia uvedeného uhla na zvislej osi je prsia zodpovedajúci tomuto uhlu.

Nižšie je (na obrázku 3) trigonometrický kruh a prsia pre niekoľko uhlových hodnôt x1, x2, x3 a x4.

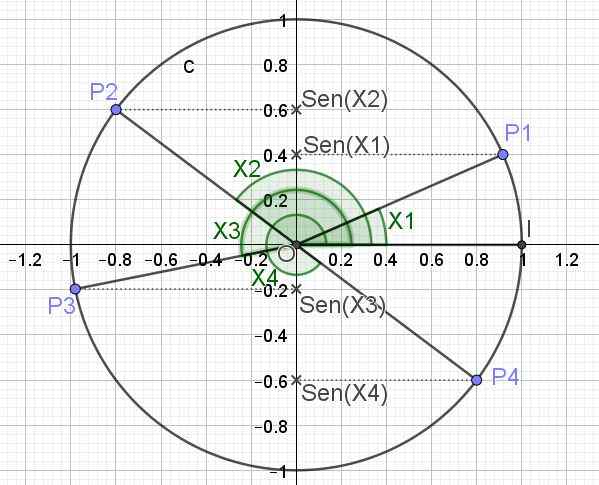Obrázok 3. Trigonometrický kruh a lona niekoľkých uhlov. (Vlastné rozpracovanie)

Definované týmto spôsobom maximálna hodnota, ktorú môže mať funkcia Sen (x), je 1, ktorá sa vyskytuje, keď x = π/2 + 2π n, je N celé číslo (0, ± 1, ± 2,). Minimálna hodnota, ktorú môže funkcia Sen (x) trvať, keď x = 3π/2 + 2π n. 

Funkcia coseno y = cos (x) je definovaná podobným spôsobom, ale projekcia uhlových polohy p1, p2 atď. Sa vykonáva na horizontálnej osi trigonometrického kruhu.

Na druhej strane, funkcia y = tan (x) je pomer medzi funkciou sínusov a funkciou kosínu.

Potom je zobrazený graf transcendentných funkcií Sen (x), cos (x) a tan (x)

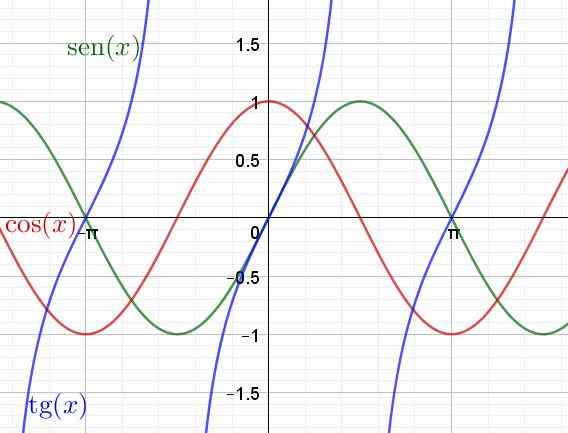Obrázok 4. Graf transcendentných funkcií, prsníka, kosínus a tangens. (Vlastné rozpracovanie)

Odvodený a integrálny

Odvodené z exponenciálnej funkcie

Derivát a ' exponenciálnej funkcie y = a^x Je to funkcia A^x znásobené ním Neperiánsky logaritmus základne a:

Môže vám slúžiť: Sada Teória: Charakteristiky, prvky, príklady, cvičenia

a '= (a^x)' = a^x ln a

V konkrétnom prípade základne a, Derivát exponenciálnej funkcie je samotná exponenciálna funkcia.

Integrál exponenciálnej funkcie

Neurčitý integrál A^x Je to funkcia rozdelená medzi neperiánsky logaritmus základne. 

V konkrétnom prípade základne E je integrál exponenciálnej funkcie samotná exponenciálna funkcia.

Derivát a integrálna tabuľka transcendentných funkcií

Nižšie je uvedená súhrnná tabuľka hlavných transcendentných funkcií, jej derivátov a neurčitých (antiderivatí):

Neurčitý derivát a integrálna tabuľka pre niektoré transcendentné funkcie. (Vlastné rozpracovanie)

Príklady

Príklad 1

Nájdite výslednú funkciu zloženia funkcie f (x) = x^3 s funkciou g (x) = cos (x):

(f alebo g) (x) = f (g (x)) = cos³(X)

Jeho derivát a jeho neurčitý integrál je:

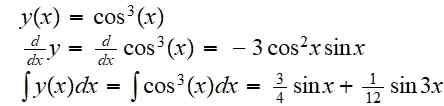
Príklad 2

Nájdite zloženie funkcie g s funkciou F, pričom sú G a F funkcie definované v predchádzajúcom príklade:

(g alebo f) (x) = g (f (x)) = cos (x³)

Je potrebné poznamenať, že zloženie funkcií nie je komunitatívna operácia.

Derivát a neurčitý integrál pre túto funkciu sú: respektíve:

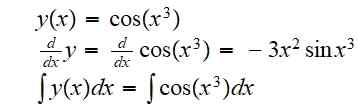
Integrál bol ponechaný, pretože nie je možné napísať výsledok ako kombinácia elementárnych funkcií presným spôsobom.

Odkazy

1. Počet jednej premennej. Ron Larson, Bruce H. Edward. Cengage Learning, 10. novembra. 2008
2. Implicitná veta funkcie: história, teória a aplikácie. Steven G. Krantz, Harold R. Parky. Springer Science & Business Media, 9. novembra. 2012
3. Multivariabilná analýza. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13. decembra. 2010
4. Dynamika systému: modelovanie, simulácia a riadenie mechatronických systémov. Dekan c. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7. marca. 2012
5. Kalkul: Matematika a modelovanie. William Bauldry, Joseph R. Fiedler, Frank r.Giordano, Ed Lodi, Rick Vitay. Addison Wesley Longman, 1. januára. 1999
6. Wikipedia. Transcendentná funkcia. Obnovené z: je.Wikipedia.com