Skutočná skutočná premenná funkcia a jej grafická reprezentácia

A Skutočná skutočná premenná funkcia Vezmite si číslo patriace do súboru reálnych čísel a priradí ho k inej hodnote, tiež skutočnej, prostredníctvom jedinečného pravidla korešpondencie. To znamená, že skutočné číslo prostredníctvom tohto pravidla získa jedinečný obraz.

Numerické premenné odchodu sú zvyčajne označené písmenom X, zatiaľ čo ich obraz je písmeno a. Na druhej strane, do pravidla korešpondencie, ktoré ich spája.  V kompaktnom zápise je napísaný:

f: x → y = f (x)

postava 1. Graf skutočnej polynómovej funkcie

Do premennej  X to sa nazýva nezávislá premenná, kým a Je to závislá premenná. Funkciu je možné vyjadriť niekoľkými spôsobmi, napríklad prostredníctvom matematického vyhlásenia, ako je táto:

• f (x) = 2x -3
• H (x) = −3x²
• 

Ďalšia forma výrazu je prostredníctvom grafu, ktorý je veľmi užitočný, pretože vám umožňuje oceniť správanie funkcie jedného pohľadu. Budovanie grafu je veľmi jednoduché pomocou karteziánskeho súradnice, v ktorom sú rovesníci [x, f (x)] reprezentované ako body v rovine. Potom sa spoja mäkkou a kontinuálnou čiarou, môžete vidieť, aká je funkcia.

Príklady

Ak chcete zostaviť graf, môžete sa uchýliť k tabuľke hodnôt, v ktorých sú umiestnené body na graf. Pre hodnoty premennej x sú vybrané, ktoré patria do domény funkcie, to znamená tie, ktoré pri výmene vo vzorci zase zobrazujú reálne čísla.

Akonáhle sú zvolené hodnoty x, určí sa jeho obraz y = f (x), a tak sa získajú bodové páry [x, f (x)], ktoré budú grafické.

Môže vám slúžiť: Homografická funkcia: Ako graf, vyriešené cvičenia

Existujú niektoré body, ktoré sú dôležité a mali by byť zahrnuté do tabuľky: tie, v ktorých sa graf odrezáva na súradnicové osi, že ak existujú, pretože nie všetky funkcie ich pretínajú.

Ak ich chcete vypočítať, postupujte takto:

-Križovatka s osou a: x = 0 sa vyrába vo vzorci funkcie a vypočíta sa zodpovedajúca hodnota.

-Križovatka s osou x: Y = 0 je hotový a rovnica f (x) = 0 je vyriešená.

Ďalej je kreslený karteziánsky súradnicový systém a každý z bodov je vynesený do grafu, ktoré sú potom spojené s mäkkou a kontinuálnou čiarou, ak je to možné.

Príklad 1

Zostavte tabuľku hodnôt a graf nasledujúcej funkcie:

f (x) = x² −4

Pred začiatkom musíte nájsť doménu funkcie, ktorá je množinou skutočných hodnôt, pre ktoré táto funkcia existuje. Pretože ide o kvadratickú funkciu, akákoľvek hodnota x, ktorá patrí do skutočných čísel, má skutočný obraz podľa F (x).

Potom je možné tabuľku zostaviť výberom akejkoľvek hodnoty x a najjednoduchšou vecou je začať s križovatkami grafu so sekami, ak existujú. Po ich nájdení potom sa snažia vyplniť stôl ďalšie body.

Pre x = 0

f (0) = -4

Preto je prvým bodom v tabuľke (0, -4). Toto je priesečník grafu s osou a.

Pre y = 0

Potom sa vykoná y = 0 a rovnica, ktorá je vyriešená, je vyriešená:

X² −4 = 0

X² = 4

Riešenia tejto rovnice sú: x₁= 2 a x₂= -2. Preto existujú dve križovatky s osou X, ktoré sú bodmi: (-2,0) a (2.0).

Môže vám slúžiť: perfektné čísla: Ako ich identifikovať a príklady

Teraz nájdete viac bodov, ktoré môžete pridať do tabuľky hodnôt:

Pre x = 1

f (1) = (1)² - 4 = −3

Pre x = - 1

f (−1) = (−1)² - 4 = −3

Pre x =  3

f (3) = (3)² - 4 = 5

Pre x =  -3

f (-3) = (−3)² - 4 = 5

Tabuľka hodnoty

Nasledujúca tabuľka ukazuje získané body, ktoré budú slúžiť na zostavenie grafu F (x):

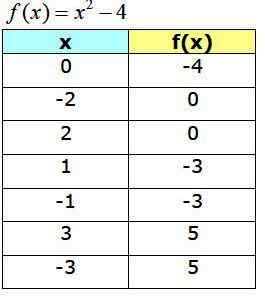Funkčný graf f (x) = x² −4

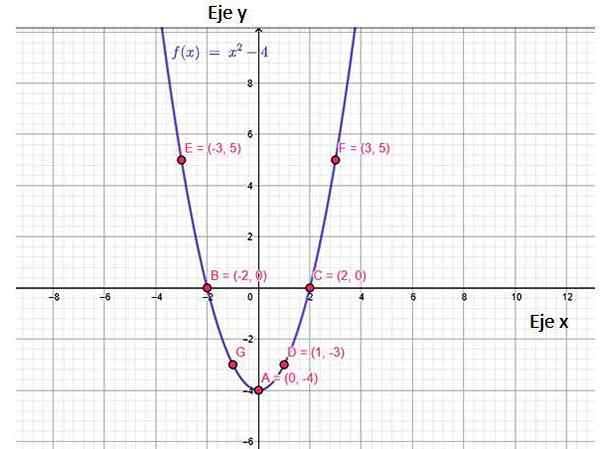Obrázok 2. Funkcia F (x) Funkčný graf, ktorý ukazuje niektoré body, ktoré k nemu patria, vrátane križovatiek so osami. Zdroj: f. Zapata, cez Geogebra.

Graf tejto funkcie je podobenstvo, ktoré sa otvára a má minimálny bod, nazývaný vrchol, súradníc (0, −4). Je zaujímavé poznamenať, že hodnoty f (x) začínajú na y = -4 až ∞. Toto je rozsah funkcia.

Z grafu je možné dospieť k záveru, že funkcia je kontinuálna, klesá v intervale (−∞, 0) a odtiaľ sa zvyšuje.

Príklad 2

Ak má graf funkcie, je možné poznať jej doménu, jej rozsah, križovatky, ktoré má so osami a vizualizujte jej všeobecné správanie (rast a zníženie).

Nižšie je uvedený graf polynomiálnej funkcie:

f (x) = - x⁴+4x²+1

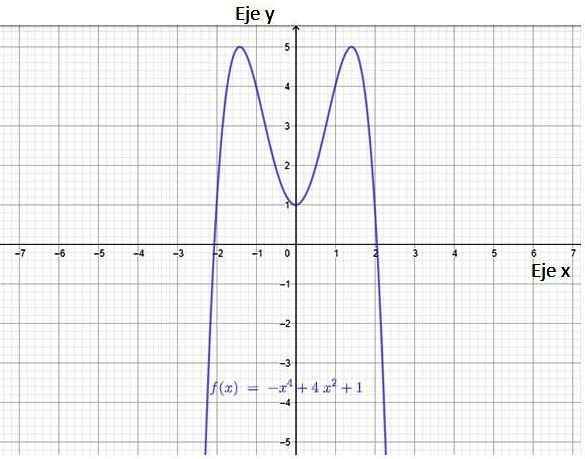Obrázok 3. Graf polynomiálnej funkcie. Zdroj: f. Zapata cez geogebra.

Z obrázka vyplýva, že funkcia má dve križovatky s osou X, bodmi (-2,0) a (2.0). Má tiež križovatku s osou y, bod (0,1).

Doménou polynomiálnej funkcie je úplná sada reálnych čísel, je tiež varovaná, že funkcia je kontinuálna a má symetriu okolo vertikálnej osi. V skutočnosti je možné overiť, že táto funkcia je Symetria pre. Funkcia je, aj keď spĺňa:

Môže vám slúžiť: zelená veta, demonštrácia, aplikácie a cvičenia

f (x) = f (-x)

Čitateľ môže overiť, že nahradením -x vo funkcii nie je zmenený.

Existujú dva zaujímavé body, ktoré sú vo výške y = 5, sú maximálne hodnoty funkcie. Rozsah tejto funkcie, to znamená sada hodnôt, ktoré premenná má a, siaha z -∞ na y = 5 presne.

Ak chcete poznať hodnoty X, ktorých obraz je y = 5, táto hodnota sa nahradí vo funkcii:

5 = - x⁴+4x²+1

A táto rovnica sa získa:

- X⁴ + 4x² - 4 = 0

Ktorých riešenia sú −√2 a + √2. Funkcia je:

-Rastúci Z x -∞ do x = −√2

-Klesajúci Z x = −√2 do x = 0

-Rastúci Z x = 0 do x = + √2

-Klesajúci Od x = + √2.

Cvičenie

Zostavte graf nasledujúcej funkcie:

f (x) = √ (x-5)

Riešenie

Najprv musíte určiť doménu funkcie, aby ste vedeli, ktoré hodnoty X je možné zvoliť na zostavenie tabuľky. V prípade navrhovanej funkcie musí byť množstvo v koreni vždy kladné alebo rovné 0, preto:

x - 5 ≥ 0

x ≥ 5

Preto je možné pre tabuľku zvoliť iba hodnoty väčšie alebo rovné 5. Pokiaľ ide o križovatky s súradnicovými osami, jedinou možnosťou je urobiť y = 0 a potom x = 5.

Je zbytočné robiť x = 0 pre túto funkciu, pretože táto hodnota nepatrí do domény.

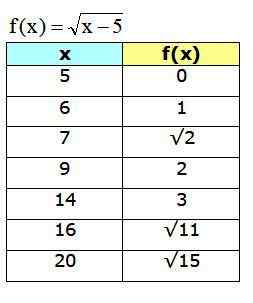
Získaný graf je:

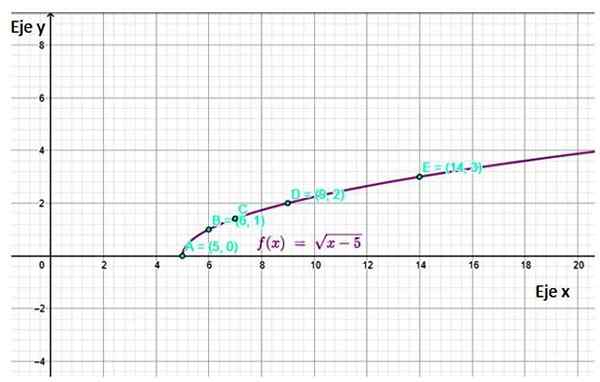Obrázok 4. Funkčný graf f (x) zobrazujúci niektoré body vypočítané v tabuľke. Zdroj: f. Zapata cez geogebra.

Odkazy

1. E-mata. Typy funkcií. Získané z: emathzone.com.
2. Hoffman, J.G. Výber matematických problémov. Edimatizovať. Sphinx.
3. Matematika je zábava. Odkaz na funkcie Commons. Získané z: Mathisfun.com.
4. Requena, b. Vesmír. Typy funkcií. Získané z: Universoformulas.com.
5. Stewart, J. 2006. Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.