Injekčná funkcia, z čoho pozostáva, na čo je to a príklady

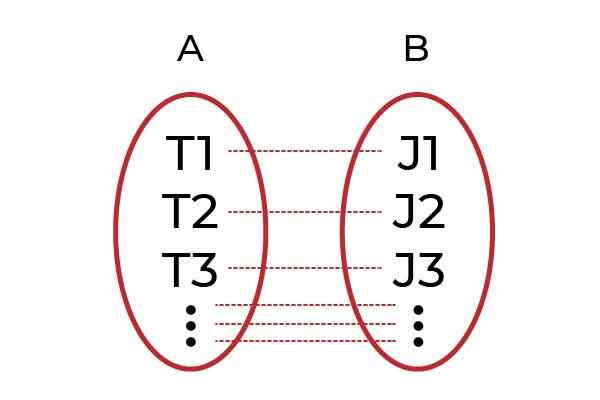
A Injekčná funkcia Je to akýkoľvek vzťah prvkov domény s jediným prvkom kodomínium. Tiež známa ako funkcia jeden za druhým ( jedenásť ) sú súčasťou klasifikácie funkcií týkajúcich sa spôsobu, akým sú ich prvky spojené.

Prvok kodomínium môže byť iba obrazom jediného prvku domény, týmto spôsobom sa hodnoty závislej premennej nemožno opakovať.

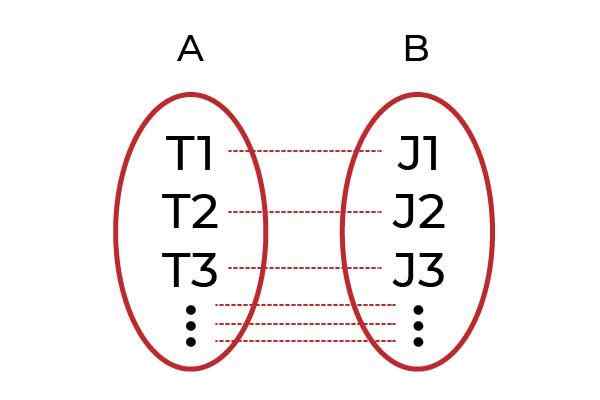Zdroj: autor.

Jasným príkladom by bolo zoskupenie mužov s prácou v skupine A a v skupine B pre všetkých šéfov. Funkcia F Bude to ten, ktorý spája každého pracovníka so svojím šéfom. Ak je každý pracovník spojený s iným šéfom cez F, tak F  Bude to jeden Injekčná funkcia.

Zvážiť Injekčný Na funkciu sa musí splniť nasledujúce:

∀ x₁  ≠ x₂   ⇒ f (x₁ ) ≠ f (x₂ )

Toto je algebraický spôsob, ako povedať Pre všetkých x₁ odlišné od x₂ Máte f (x₁ ) Odlišné od f (x₂ ).

[TOC]

Čo sú injekčné funkcie pre?

Injektivita je vlastnosť kontinuálnych funkcií, pretože zabezpečujú pridelenie obrazov pre každý prvok domény, základný aspekt v kontinuite funkcie.

Pri kreslení čiary rovnobežnej s osou X Na grafe injektívnej funkcie by sa mal dotýkať iba grafu v jednom bode, bez ohľadu na to, akú výšku alebo veľkosť A Čiara je nakreslená. Toto je grafický spôsob, ako dokázať injektivitu funkcie.

Iný spôsob, ako otestovať, či je funkcia Injekčný, Vyčistí nezávislú premennú X Pokiaľ ide o závislú premennú A. Potom by sa malo overiť, či doména tohto nového výrazu obsahuje reálne čísla, súčasne ako pre každú hodnotu A existuje jedna hodnota X.

Objednávacie funkcie alebo vzťahy dodržiavajú okrem iného zápis F: D_F→C_F

To znie F, ktoré ide od D_F do c_F

Kde funkcia F Vzťahovať sady Oblasť a Kodominium. Tiež známy ako štartovacia sada a príchod.

Môže vám slúžiť: náhodné odber vzoriek: metodika, výhody, nevýhody, príklady

Dominion D_F  Obsahuje povolené hodnoty pre nezávislú premennú. Kodomínium C_F  Tvorí sa všetkými dostupnými hodnotami do závislej premennej. Prvky C_F v súvislosti s D_F  Vedia ako Rozsah funkcií (r_F ).

Kondicionovanie funkcií

Niekedy funkcia, ktorá nie je injektívna, môže podstúpiť určité kondicionovanie. Tieto nové podmienky môžu zmeniť na a Injekčná funkcia. Všetky druhy modifikácií domény a kodomínium funkcie sú platné, kde cieľom je splniť vlastnosti injektivity v príslušnom vzťahu.

Príklady injekčných funkcií s vyriešenými cvičeniami

Príklad 1

Byť funkciou F: r → R definovaný riadkom F (x) = 2x - 3

Odpoveď: [všetky skutočné čísla]

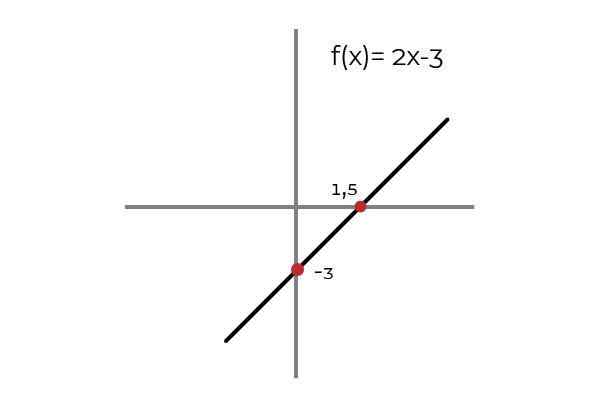Zdroj: autor.

Zistilo sa, že pre akúkoľvek hodnotu domény je v kodomínii obraz. Tento obrázok je jedinečný, vďaka čomu je injektívna funkcia. Platí to pre všetky lineárne funkcie (funkcie, ktorých väčší stupeň premennej je jeden).

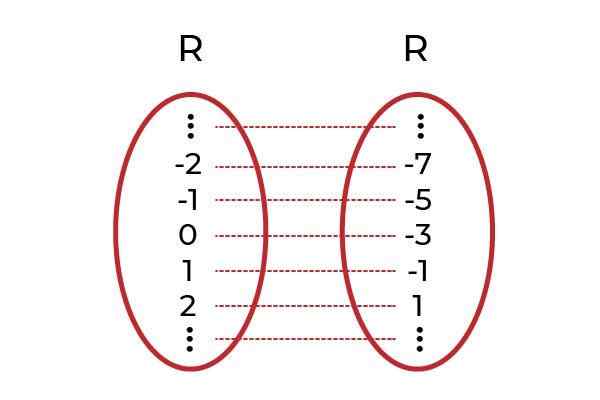Zdroj: autor.

Príklad 2

Byť funkciou F: r → R definovaný F (x) = x² +1

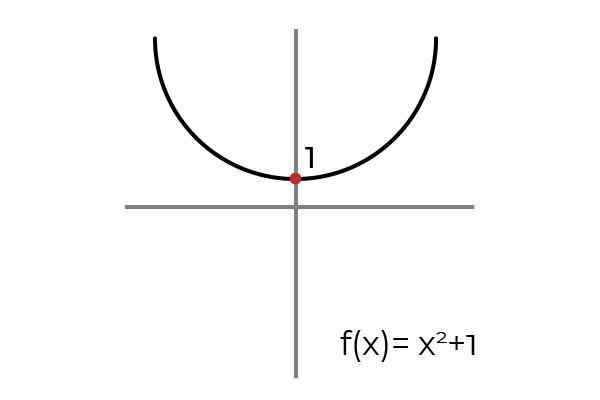Zdroj: autor

Pri kreslení vodorovnej čiary sa zistí, že graf sa nachádza pri viac ako jednej príležitosti. Z tohto dôvodu funkcia F nie je injekčný, zatiaľ čo je definovaný  R → R

Doména funkcie je podmienená:

                                               F: r⁺ Alebo 0 → R

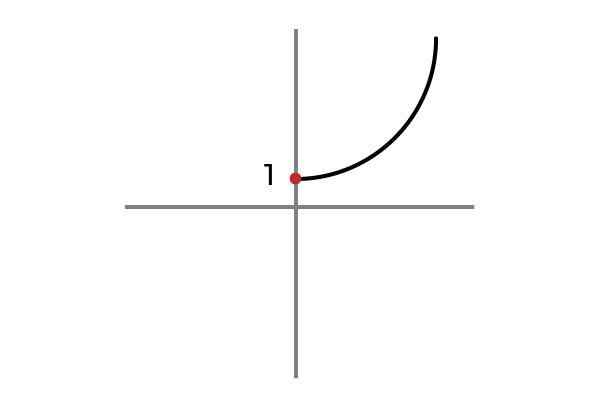Zdroj: autor

Teraz nezávislá premenná neberie záporné hodnoty, týmto spôsobom sa zabráni opakovaniu výsledkov a funkcie F: r⁺ Alebo 0 → R definovaný F (x) = x² + 1 je injekčný.

Ďalším homológnym riešením by bolo obmedziť doménu naľavo, to znamená, že funkciu obmedzuje iba na záporné a nulové hodnoty.

Doména funkcie je podmienená

                                               F: r^- Alebo 0 → R

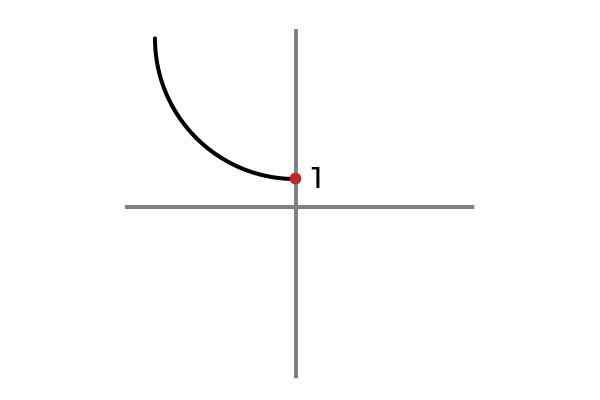Zdroj: autor

Teraz nezávislá premenná neberie záporné hodnoty, týmto spôsobom sa zabráni opakovaniu výsledkov a funkcie F: r^- Alebo 0 → R definovaný F (x) = x² + 1 je injekčný.

Trigonometrické funkcie majú správanie podobné vlnám, kde je veľmi bežné nájsť opakovania hodnôt v závislej premennej. Prostredníctvom špecifického kondicionovania na základe predchádzajúcich znalostí týchto funkcií môžeme obmedziť doménu tak, aby spĺňala podmienky injekcie.

Môže vám slúžiť: Coplanares body: rovnica, príklad a vyriešené cvičenia

Príklad 3

Byť funkciou F: [ -π/2, π/2 ] → R definovaný F (x) = cos (x)

V intervale [ -π/2 → π/2 ] Kozínová funkcia mení svoje výsledky medzi nulou a jedným.

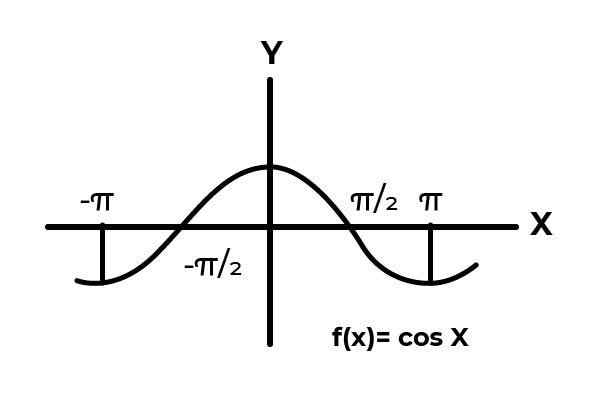Zdroj: autor.

Ako je vidieť v grafiku. Začnite od nuly x = -π/2 a potom dosiahnutie maxima nula. Je to po x = 0 že hodnoty sa začínajú opakovať, až kým sa nevrátia na nulu v x = π/2. Týmto spôsobom je to známe F (x) = cos (x) nie je injekčný Pre interval [ -π/2, π/2 ] .

Pri štúdiu funkčnej grafiky F (x) = cos (x) Intervaly sa pozorujú, keď sa správanie krivky prispôsobuje kritériám injektivity. Ako je interval

[0 , π ]

Ak sa funkcia mení výsledky od 1 do -1, bez opakovania akejkoľvek hodnoty v závislej premennej.

Týmto spôsobom funkcia funkcie F: [0 , π ] → R definovaný F (x) = cos (x). Je to injekčné

Existujú nelineárne funkcie, v ktorých sú uvedené podobné prípady. V prípade racionálnych výrazov, kde sa v menovateľovi uvádza aspoň jedna premenná, existujú obmedzenia, ktoré bránia injektvivite vzťahu.

Príklad 4

Byť funkciou F: r → R definovaný F (x) = 10/x

Funkcia je definovaná pre všetky skutočné čísla okrem 0 Kto predstavuje neurčitosť (nemožno ju rozdeliť medzi nulu).

Keď sa blíži nula vľavo, závislá premenná má veľmi veľké záporné hodnoty a bezprostredne po nule hodnoty závislej premennej majú veľké kladné čísla.

Toto narušenie robí výraz F: r → R definovaný F (x) = 10/x

Nebuď injekčný.

Ako je vidieť v predchádzajúcich príkladoch, vylúčenie hodnôt v doméne slúži na „opravu“ týchto neurčitých neurčení. Nula je vylúčená z domény, pričom súpravy sada a príchod definované nasledovne:

R - 0 → R

Kde R - 0 symbolizuje skutočný s výnimkou sady, ktorej jediný prvok je nula.

Týmto spôsobom výraz F: r - 0 → R definovaný F (x) = 10/x je injekčný.

 Príklad 5

Byť funkciou F: [0 , π ] → R definovaný F (x) = sin (x)

V intervale [0 , π ] Funkcia sínusu mení svoje výsledky medzi nulou a jedným.

Môže vám slúžiť: náhodná premenná: koncept, typy, príklady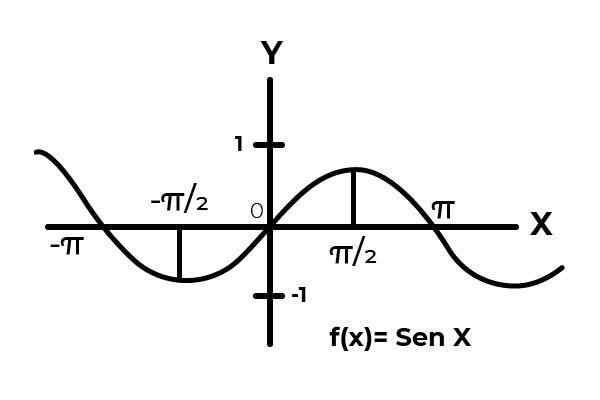Zdroj: autor.

Ako je vidieť v grafiku. Začnite od nuly x = 0 potom dosiahnutie maxima v x = π/2. Je to po x = π/2, že hodnoty sa začnú opakovať, až kým sa nevrátia na nulu v x = π. Týmto spôsobom je to známe F (x) = sin (x) nie je injekčný Pre interval [0 , π ] .

Pri štúdiu funkčnej grafiky F (x) = sin (x) Intervaly sa pozorujú, keď sa správanie krivky prispôsobuje kritériám injektivity. Ako je interval  [  π/2,3π/2  ]

Ak sa funkcia mení výsledky od 1 do -1, bez opakovania akejkoľvek hodnoty v závislej premennej.

Týmto spôsobom funkcia F: [  π/2,3π/2  ] → R definovaný F (x) = sin (x). Je to injekčné

Príklad 6

Overte, či je funkcia F: [0, ∞) → R definovaný F (x) = 3x² Je to injekčné.

Pri tejto príležitosti je doména výrazu už obmedzená. Zistilo sa tiež, že závislé premenné hodnoty sa v tomto intervale neopakujú.

Preto možno dospieť k záveru F: [0, ∞) → R definovaný F (x) = 3x²   Je to injekčné

Príklad 7

Identifikujte, ktorá z nasledujúcich funkcií je

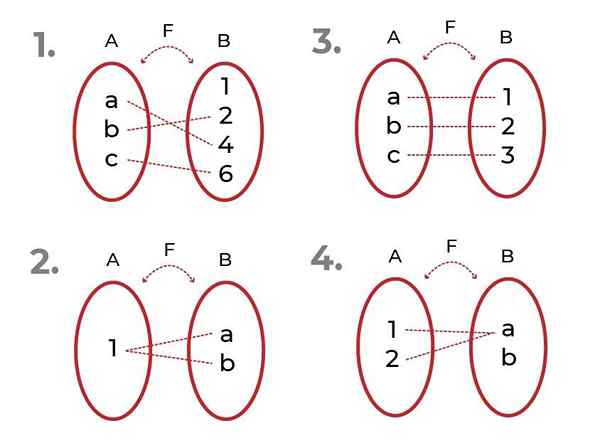Zdroj: autor

1. Je to injekčné. Súvisiace prvky kodomínium sú jedinečné pre každú hodnotu nezávislej premennej.
2. Nie je to injekčné. Existujú prvky co -oomínium spojené s viac ako jedným prvkom počiatočnej sady.
3. Je to injekčné
4. Nie je to injekčné

Navrhované cvičenia pre triedu/dom

Overte, či sú nasledujúce funkcie injekčné:

F: [0, ∞) → R definovaný F (x) = (x + 3)²  

F: [ π/2,3π/2  ] → R definovaný F (x) = tan (x)

F: [ -π,π  ] → R definovaný F (x) = cos (x + 1)

F: r → R definovaný riadkom F (x) = 7x + 2

Odkazy

1. Úvod do logiky a kritického myslenia. Merrilee H. Losos. University of Pittsburgh
2. Problémy v matematickej analýze. Piotr Bilar, Alfred Witkowski. Wroclaw University. Pól.
3. Prvky abstraktnej analýzy. Mícheál O'Searcoid PhD. Oddelenie matematiky. University College Dublin, Beldfield, Dublind 4.
4. Úvod do logiky a metodológie deduktívnych vied. Alfred Tarski, New York Oxford. Oxford University Press.
5. Matematické analýzy. Enrique Linés escardó. Redaktor. Do roku 1991. Barcelona, ​​Španielsko.