Vlastnosti funkcie rozloženej funkcie, príklady, cvičenia

Ten rozložená funkcia y = s (x) je funkcia definovaná v kusoch alebo častiach, takže v konečnom intervale [a, b] má konečný počet diskontinuít, ktoré nazývame x₀ < x₁ < x₂ <… . x_n.  V každom otvorenom intervale (x_Jo , X_i+1) a má konštantnú hodnotu hodnoty S_Jo, S diskontinuitami -Saltos- v bodoch X_Jo.

Graf, ktorý je výsledkom takejto funkcie, pozostáva z krokov alebo krokov. Pozrime sa na príklad nižšie:

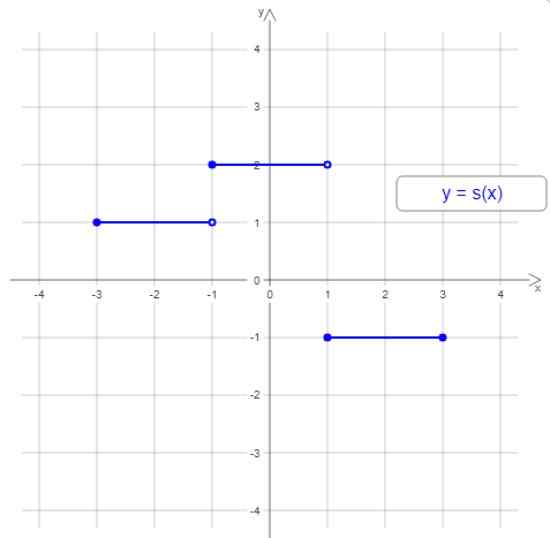
postava 1. Príklad rozloženej funkcie. Zdroj: Wikimedia Commons.

Graf tejto stupňovej funkcie má tri kroky alebo rozložené intervaly, ale vo všeobecnosti môže mať funkcia s rozloženou funkciou akékoľvek kroky. Šírka krokov sa môže líšiť a schodisko nie je vždy stúpajúce alebo zostupné.

Rozdelená funkcia príkladu je možné napísať špecifikujúcou šírku a vysoký z každého kroku, ako je tento:

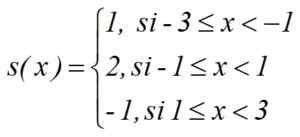
[TOC]

Charakteristiky stupňovej funkcie

-Funkcia prijíma svoj názov podľa grafu vo forme krokov, ktoré sú uvedené v segmentoch, ktoré ho tvoria. Každý segment má časť domény funkcie a v každej z nich je funkcia konštantná.

-Doménou rozloženej funkcie sú hodnoty, ktoré patria do intervalu, pre ktoré je definovaná: [a, b], zatiaľ čo rozsah je tvorený hodnotami s_Jo výšok krokov.

V príklade na obrázku 1 je doména interval [-3,3] a rozsah je hodnoty -1, 1 a 2.

-Rozložená funkcia je kontinuálna, s výnimkou hodnôt, ktoré vymedzujú každý krok, body x_Jo.

-Funkcie Escalonada sa dajú pridať a vynásobiť, aby sa vznikli novým stupňovým funkciám.

-Jeho derivát je 0 pre body, v ktorých je definovaný, pretože v nich je funkcia konštantná. Derivát neexistuje v diskontinuitách.

-Integrál stupňovej funkcie s (x) medzi do a b Existuje a zodpovedá súčtu oblastí obdĺžnikov šírky x_Jo- X_I-1 a výška s_{klimatizovať}, rovná kroku.

Môže vám slúžiť: Nezávislé udalosti: demonštrácia, príklady, cvičenia

Pretože oblasť obdĺžnika je produktom základne podľa výšky, musíme:

Príklady rozložených funkcií

V rámci rozložených funkcií existuje niekoľko typov, napríklad funkcie celá časť a funkcia Jednotlivý krok, ako aj rôzne rozložené funkcie, ktoré opisujú spoločné situácie, ako napríklad miery mnohých služieb. Pozrime sa na niekoľko príkladov:

- Príklad 1: Celé strany

Funkcia celej časti často používa dvojitú kategóriu:

f (x) = [[x]]

A je definovaná ako funkcia, ktorá priraďuje každému skutočnému číslu najbližšie alebo menšie celé číslo a ignoruje akékoľvek desatinné číslo, ktoré má číslo. Ako to môže byť, máme:

Funkcia strechy alebo oblohy

Priraďuje každej hodnote domény najbližšie celé číslo prebytkom. Napríklad:

[[+2.56]] = 3

Desatinná časť, ktorá je 0, sa ignoruje.56 a najbližšie celé číslo je priradené, ktoré je väčšie ako 2.

Ďalší príklad:

[[-4.2]]= -3

Opäť je desatinná časť 0 vynechaná.2 a najvyššie najväčšie celé číslo bližšie k -4 sa považuje za hodnotu funkcie, ktorá je -3.

Na nasledujúcom obrázku je graf funkcie stropu, všimnite si, že krok je vymedzený malým dutým kruhom doľava a jeden plný doprava, pretože akékoľvek číslo intervalu je najväčšie celé číslo priradené medzi koncami medzi koncami medzi koncami medzi koncami končí medzi koncami intervalu.

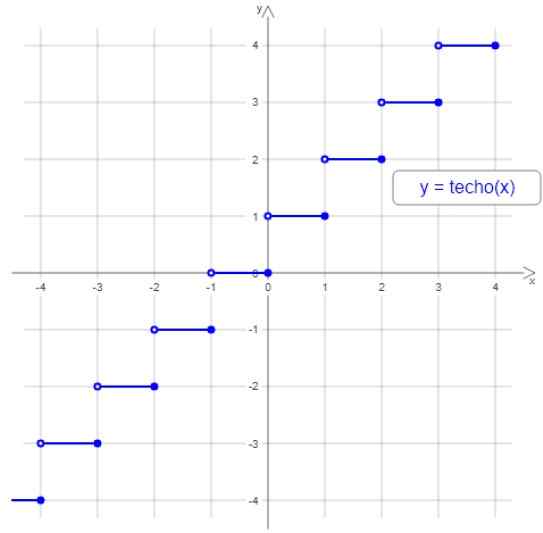Obrázok 2. Funkcia strechy alebo oblohy. Zdroj: Wikimedia Commons.

Napríklad, všetky hodnoty medzi 3 a 4 sú priradené celé 4, ktoré sú medzi -2 a -1, sú priradené -1 atď.

Funkcia podlahy alebo pôdy

Priraďuje každej hodnote domény najbližšie celé číslo predvolene. Príklady tejto funkcie sú:

Môže vám slúžiť: Koľko desatín je v jednotke?

[[+3.7] = 3

[-1.5] = -2

[[π]] = 3

Obe funkcie sú kontinuálne, s výnimkou celých čísel, kde sú prezentované skoky, a sú konštantné pre hodnoty medzi celkovými číslami K a K+1.

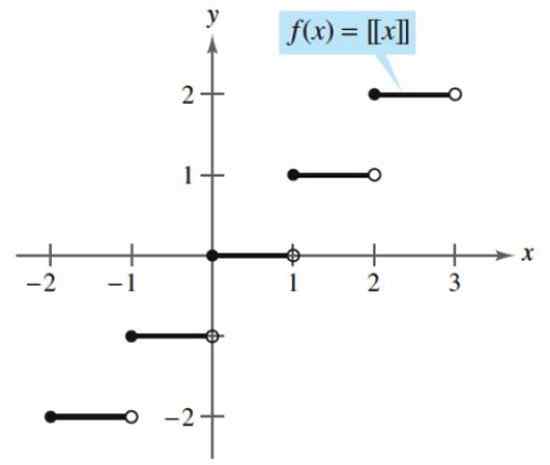Obrázok 3. Funkcia podlahy alebo pôdy. Zdroj: Larson, r. Výpočet premennej.

- Príklad 2

V meste je sadzba taxíkov 3.65 dolárov, za prvých 100 m. A každých 100 m je 0.18 dolárov, čo je limit na cestu 50 km.

Je potrebné stanoviť funkciu, ktorá sa týka trasy v metroch s nákladmi na službu o $, ktorá musí mať tento formulár:

f (x) = 3.65 + 0.18. [[X /100]] $

Kde môže byť celá funkcia časti funkcie oblohy, ku ktorej sa pridá základná rýchlosť 3.65 dolárov. Napríklad, ak chceme vedieť, koľko bude zaplatená za cestu 6.25 km = 6250 m, budeme mať:

f (x) = 3.65 + 0.18. [[x /100]] $ = 3.65 + 0.18 . [[6250/100]] $ = 3.65 + [[11.25]] $ = 15.65 dolárov

Ak si taxíková spoločnosť vyberie funkciu podlahy, klient by za cestu zaplatil o niečo menej:

f (x) = 3.65 + 0.18. [[x /100]] $ = 3.65 + 0.18 . [[6250/100]] $ = 3.65 + [[11.25]] $ = 14.65 dolárov

Vyriešené cvičenia

- Cvičenie 1

Hovory na veľké vzdialenosti medzi mestami A a B Cena 0.40 dolárov 10 minút. Po tomto období je zlomok alebo ďalšia minúta hodnota 0.05 $.

Vyjadrite náklady C (t) volania, ktoré trvá určité množstvo minút.

Riešenie

Túto funkciu môžeme vyjadriť, ak analyzujeme, čo sa stane s každou možnosťou počas trvania hovoru:

Pre t ≤ 10 minút

Keď je T, čo je čas, ktorý hovor trvá, je menší alebo rovný 10 minút, platí sa 0.40 dolárov.

Môže vám slúžiť: 2 -digitové divízie vyriešené

Preto:

f (t) = 0.40 dolárov za T zahrnuté medzi 0 a 10 minútami.

Už máme časť funkcie.

Pre t> 10 minút

ENTERO T PRÍPAD

Teraz sa pozrime, čo sa stane, keď je prekročený čas t = 10 minút: Môže sa stať, že prebytok je celé číslo, napríklad, že konverzácia trvá presne 11, 12, 13, 14 minút alebo viac. V takom prípade bude výška hovoru:

f (t) = 0.40 + 0.05 (t-10) $, pre t viac ako 10 minút, s celkovým t.

To znamená, že v tomto prípade: t = 11, 12, 13, 14, 15 ... minúty.

Predpokladajme, že konverzácia trvá presne 15 minút, cena bude:

f (15) = 0.40 + 0.05 (15-10) $ = 0.65 dolárov

Desatinné miesto

Nakoniec zvážte prípad, v ktorom hovor vydrží na čas s desatinnou časťou. Predpokladajme napríklad, že hovor trvá 15 minút a 45 sekúnd, čo by bolo decimálne 15.75 minút.

Môžeme to vyjadriť z hľadiska celej časti typu podlahy za predpokladu, že spoločnosť chce poskytnúť klientovi alebo oblohe viac výhod:

f (t) = 0.40 + 0.05 ⋅ [[T-9]] $

Pozrime sa, čo by klient zaplatil, ak by to bola funkcia podlahy:

F (15.75) = 0.40 + 0.05 ⋅ [15.75-9]] $ = 0.40 + 0.05lek [[6.75]] $ = 0.40 + 0.05 × 6 $ = 0.70 dolárov.

Alebo ako funkcia oblohy, v takom prípade by náklady boli:

F (15.75) = 0.40 + 0.05 [[15.75-9]] $ = 0.40 + 0.05lek [[6.75]] $ = 0.40 + 0.05 × 7 $ = 0.75 $.

Funkcia

Ako funkcia definovaná časťami je:

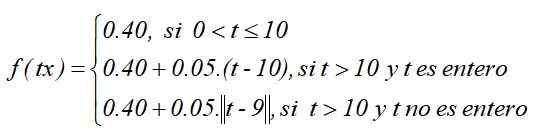
Graf funkcie by bol taký, za predpokladu, že bola vybraná celá funkcia typu stropu:

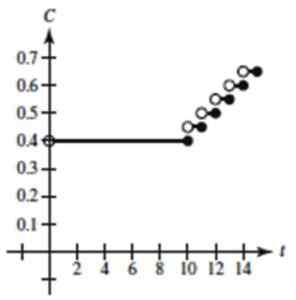Obrázok 4. Graf stupnickej funkcie cvičenia vyriešil 1. Zdroj: Larson, r. Výpočet premennej.

- Cvičenie 2

Vypočítajte integrálny ∫s (x) dx medzi -3 a 3 stupňovej funkcie:

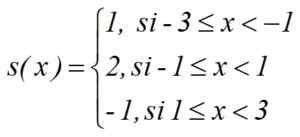
Riešenie

Použijeme definíciu pre integrál funkcie rozloženej:

Preto je integrál hľadaný I je:

I = 1. [(-1)-(-3)] + 2.[1- (-1)]+(-1).[3-1] = 2+4-2 = 4

Odkazy

1. Jiménez, r. 2006.Matematické funkcie. Pearson Vzdelanie.
2. Larson, R. 2010. Výpočet premennej. 9NA. Vydanie. McGraw Hill.
3. Matematika IV. Funkcia. Získané z: Cobaqroo.Edu.mx.
4. Wikipedia. Funkcie celej časti. Obnovené z: je.Wikipedia.orgán.
5. Wikipedia. Rozložená funkcia. Obnovené z: je.Wikipedia.orgán.