Bijektívna funkcia Čo je, ako sa to robí, príklady, cvičenia
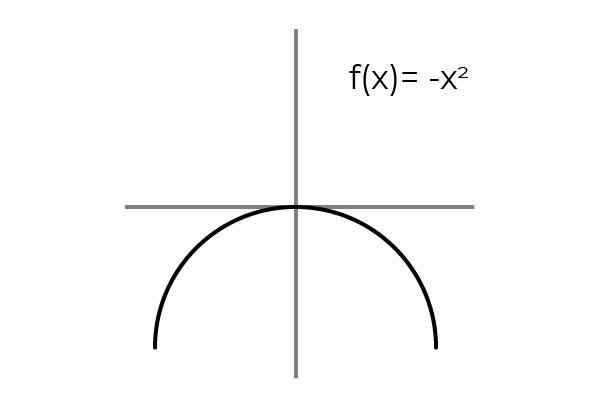
- 4369
- 341
- Denis Škriniar
A Bijektívna funkcia Je to ten, ktorý spĺňa dvojitý stav bytia Injekčné a nadmerné. To znamená, že všetky prvky domény majú v kodomínii jeden obraz a kodomínium sa zase rovná rozsahu funkcie ( RF ).
Splní sa, keď sa považuje za biunivookálny vzťah medzi prvkami domény a kodomínium. Jednoduchým príkladom je funkcia F: r → R definovaný riadkom F (x) = x
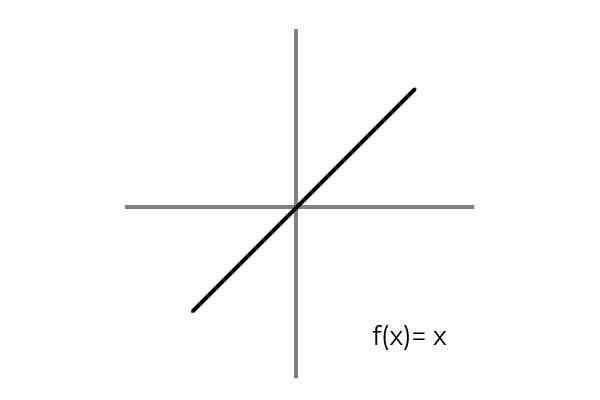 Zdroj: autor
Zdroj: autor Zistilo sa, že pre každú hodnotu domény alebo sada odchodu (obidva výrazy sa platia rovnako) v kodominium alebo príchode je jediný obrázok. Okrem toho neexistuje žiadny prvok kodominium, ktorý nie je obraz.
Tak F: r → R definovaný riadkom F (x) = x je bijective
[TOC]
Aká je funkcia bijjektívnej funkcie?
Na to, aby ste na to reagovali, je potrebné mať jasné pojmy týkajúce sa storočia Injekčnosť a Nadmerná funkcia, Okrem kritérií kondicionovania funkcií na ich prispôsobenie požiadavkám.
Injekčnosť funkcie
Funkcia je Injekčný Keď každý z prvkov jeho domény súvisí s jediným prvkom kodomínium. Prvok kodomínium môže byť iba obrazom jediného prvku domény, týmto spôsobom sa hodnoty závislej premennej nemožno opakovať.
Zvážiť Injekčný Na funkciu sa musí splniť nasledujúce:
∀ x1 ≠ x2 ⇒ f (x1 ) ≠ f (x2 )
Nadmerná funkcia
Funkcia je klasifikovaná ako Nadmerný, Ak je každý prvok jeho kodomínium obrazom aspoň jednej doménovej prvku.
Zvážiť Nadmerný Na funkciu sa musí splniť nasledujúce:
Môže vám slúžiť: náhradné odber vzoriekByť F: DF → CF
∀ B ℮ CF A do ℮ DF / F (a) = b
Toto je algebraický spôsob, ako zistiť, že pre každého „b“, ktorý patrí do CF Existuje „A“, ktorý patrí DF tak, že funkcia vyhodnotená v „A“ sa rovná „b“.
Kondicionovanie funkcií
Niekedy funkcia, ktorá nie je Bijective, môže podstúpiť určité kondicionovanie. Tieto nové podmienky môžu zmeniť na a Bijektívna funkcia. Všetky typy modifikácií domény a kodomínium funkcie sú platné, kde cieľom je splniť vlastnosti injektivity a nadmernej alcheivity v príslušnom vzťahu.
Príklady: Vyriešené cvičenia
Cvičenie 1
Byť funkciou F: r → R definovaný riadkom F (x) = 5x +1
Odpoveď: [všetky skutočné čísla]
Zistilo sa, že pre akúkoľvek hodnotu domény je v kodomínii obraz. Tento obrázok je jedinečný, čo vytvára F byť jedným Injekčná funkcia. Rovnakým spôsobom pozorujeme, že kodomínium funkcie sa rovná jej rozsahu. Tak spĺňa stav Nadmernosť.
Byť injekčný a nadmerný zároveň, že to môžeme dospieť k záveru
F: r → R definovaný riadkom F (x) = 5x +1 je a Bijektívna funkcia.
Platí to pre všetky lineárne funkcie (funkcie, ktorých väčší stupeň premennej je jeden).
Cvičenie 2
Byť funkciou F: r → R definovaný F (x) = 3x2 - 2
Pri kreslení vodorovnej čiary sa zistí, že graf sa nachádza pri viac ako jednej príležitosti. Z tohto dôvodu funkcia F Nie je injektívne, a preto to nebude Bijective Pri definovaní v R → R
Rovnakým spôsobom existujú hodnoty kodominium, ktoré nie sú obrazmi žiadneho prvku domény. Z tohto.
Môže vám slúžiť: Sada Teória: Charakteristiky, prvky, príklady, cvičeniaDoména a kodomínium funkcie sú podmienené
F: [0 , ∞] → [ - 2 , ∞ ]
Kde sa pozoruje, že nová doména pokrýva hodnoty od nuly po kladné nekonečno. Vyhnúť sa opakovaniu hodnôt, ktoré ovplyvňujú injektivitu.
Kodominium sa teda modifikoval, počíta sa od „-2“ do pozitívnej nekonečnosti, vylúčené z kodominia hodnoty, ktoré nezodpovedali žiadnemu prvku domény
Týmto spôsobom sa dá zabezpečiť F : [0 , ∞] → [ - 2 , ∞ ] definovaný F (x) = 3x2 - 2
Je to bijektívne
Cvičenie 3
Byť funkciou F: R → R definovaný F (x) = sin (x)
V intervale [ -∞ , +∞ ] Funkcia sínusu mení svoje výsledky medzi nulou a jedným.
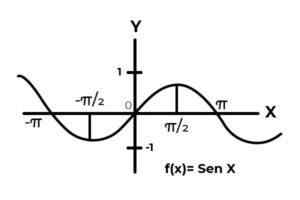 Zdroj: autor.
Zdroj: autor. Funkcia F Nezodpovedá kritériám injektivity a nadmernej prípravy, pretože závislé premenné hodnoty sa opakujú v každom π intervale. Okrem toho podmienky kodomínium mimo intervalu [-eleven] Nie sú obrazom žiadneho prvku domény.
Pri štúdiu funkčnej grafiky F (x) = sin (x) Intervaly sa pozorujú, keď správanie krivky spĺňa kritériá Bijectivita. Ako je interval DF = [ π/2,3π/2 ] Pre doménu. A CF = [-1, 1] Pre kodominium.
Ak sa funkcia mení výsledky od 1 do -1, bez opakovania akejkoľvek hodnoty v závislej premennej. A zároveň sa co -oominium rovná hodnotám prijatým výrazom Hriech
Týmto spôsobom funkcia F: [ π/2,3π/2 ] → [-1, 1] definovaný F (x) = sin (x). Je to bijektívne
Cvičenie 4
Zvýšte potrebné podmienky pre DF a cF. Takže výraz
Môže vám slúžiť: Chyba vzorkovania: vzorce a rovnice, výpočet, príkladyF (x) = -x2 Bit.
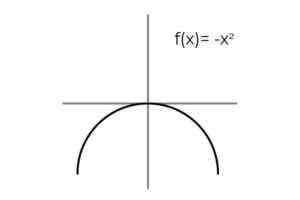 Zdroj: autor
Zdroj: autor Opakovanie výsledkov sa pozoruje, keď premenná má opačné hodnoty:
F (2) = f (-2) = -4
F (3) = f (-3) = -9
F (4) = f (-4) = -16
Doména je podmienená a obmedzuje ju na pravú stranu skutočnej čiary.
DF = [0 , +∞ ]
Rovnakým spôsobom sa pozoruje, že rozsah tejto funkcie je interval [ -∞ , 0], ktoré tým, že slúži ako kodominium.
Týmto spôsobom to môžeme dospieť k záveru
Výraz F: [0 , +∞ ] → [ -∞ , 0] definovaný F (x) = -x2 Je to bijektívne
Navrhované cvičenia
Overte, či sú nasledujúce funkcie bijektívne:
F: [0 , ∞) → R definovaný F (x) = 3 (x + 1)2 +2
F: [ 3π/2,5π/2 ] → R definovaný F (x) = 5ctg (x)
F: [ -π,π ] → R definovaný F (x) = cos (x - 3)
F: r → R definovaný riadkom F (x) = -5x + 4
Odkazy
- Úvod do logiky a kritického myslenia. Merrilee H. Losos. University of Pittsburgh
- Problémy v matematickej analýze. Piotr Bilar, Alfred Witkowski. Wroclaw University. Pól.
- Prvky abstraktnej analýzy. Mícheál O'Searcoid PhD. Oddelenie matematiky. University College Dublin, Beldfield, Dublind 4
- Úvod do logiky a metodológie deduktívnych vied. Alfred Tarski, New York Oxford. Oxford University Press.
- Matematické analýzy. Enrique Linés escardó. Redaktor. Do roku 1991. Barcelona, Španielsko.
- « Štruktúra glykogénu, syntéza, degradácia, funkcie
- Charakteristické vlastnosti enzýmov, akčné mechanizmy, príklady »

