Fyzický

Výsledná sila, ako vypočítané a vyriešené cvičenia

Výsledná sila, ako vypočítané a vyriešené cvičenia

Ten sila výsledný Je to súčet všetkých síl, ktoré pôsobia na rovnakom tele. Ak telo alebo objekt podlieha pôsobeniu niekoľkých síl súčasne, dôjde k účinku. Konanie sily môžu byť nahradené jedinou silou, ktorá má rovnaký účinok. Táto jedinečná sila je výsledná sila známa aj ako sieťová sila a je znázornená symbolom FR .

Účinok, ktorý vytvára FR Bude závisieť od jeho veľkosti, smeru a významu. Fyzikálne veľkosti, ktoré majú smer a význam, sú vektorové veľkosti.

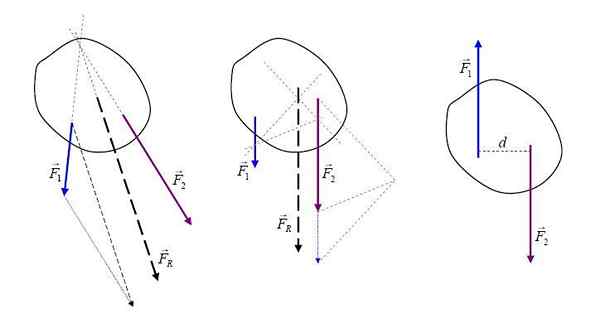Výsledné sily. Autor: Ilevanat (https: // commons.Wikimedia.org/wiki/spis: ReJultanta.JPG), z Wikimedia Commons

Byť sily, ktoré pôsobia na teleso a vektorové veľkosti, výsledná sila FR  Je to vektorový súčet všetkých síl a môže byť graficky reprezentovaný so šípkou, ktorá naznačuje jeho smer a význam.

S výslednou silou je problém tela ovplyvneného niekoľkými silami zjednodušený jeho redukciou na jednu silu pôsobiacu.

[TOC]

Vzorec

Matematické znázornenie výslednej sily je letným vektorom síl.

 FR= ∑F          (1)

 ∑F = f1+ F2+ F3+.. FN           (2)

FR= Výsledná sila

∑F = Súčet síl

N= Počet síl

Výsledná sila môže byť tiež zastúpená rovnicou Newtonovho druhého zákona.

   FR= m.do          (3)

m= telesná hmotnosť

a = zrýchlenie tela

Ak sa rovnica (1) nahradí v rovnici (3) Získajú sa nasledujúce rovnice:

∑F = m.do          (4)

F1+ F2+ F3+.. FN = m.do          (5)

Matematické výrazy (4) a (5) poskytujú informácie o stave tela získaním akcelerácie vektora do.

Ako sa vypočíta výsledná sila?

Výsledná sila sa získa pri uplatňovaní Newtonovho druhého zákona, ktorý stanovuje nasledujúce:

Môže vám slúžiť: sily na diaľku

Čistá sila pôsobiaca na telo sa rovná produktu jeho hmotnosti zrýchlením, ktoré získava. (Rovnica (3))

Zrýchlenie tela bude mať smer aplikovanej siete. Keby boli známe všetky sily pôsobiace v tele, stačilo by ho na to, aby sa získala výsledná sila, stačila by sa pridať, aby sa získala výsledná sila. Podobne, ak je známa výsledná sila, potom by ju rozdelila telom tela, aby získala jeho zrýchlenie.

Ak je výsledná sila neplatná, telo je v pokoji alebo konštantnej rýchlosti. Ak výsledná sila pôsobí na telo, jediná sila sa rovná tejto sile FR=F.

Keď niekoľko síl pôsobí na rovnakom tele, musia sa zohľadniť vektorové zložky sily, a ak sú tieto sily rovnobežné alebo nie.

Napríklad, ak vodorovne posúvame knihu umiestnenú na stole. Sily v horizontálnom smere sú jediné, ktoré poskytujú zrýchlenie tela. Vertikálna sieťová sila v knihe je nula.

Ak má aplikovaná sila na knihu sklon vzhľadom na vodorovnú rovinu tabuľky, sila je napísaná na základe vertikálnych a horizontálnych komponentov.

Výsledný paralelných síl 

Paralelné sily, ktoré pôsobia na tele, sú tie sily, ktoré pôsobia rovnakým smerom. Môžu mať dva typy rovnakého zmyslu alebo v opačnom smere.

Keď sily pôsobiace na telo majú rovnaký smer a rovnaký zmysel alebo sú v opačnom smere, výsledná sila sa získa vykonaním algebraického súčtu číselných hodnôt síl síl.

Môže vám slúžiť: elektrický tok poľa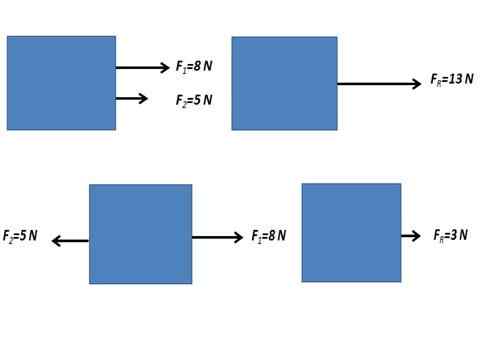Sila vyplývajúca z dvoch paralelných síl.

Neparalelné sily

Ak sa na telo aplikujú neparalelné sily, výsledné sily budú mať obdĺžnikové a vertikálne komponenty. Matematický výraz na výpočet čistej sily je:

FR2= (∑ fX)2+(∑ fa)2            (6)

tak θX= ∑ fa / ∑ fX         (7)

∑ fX  a ∑ fX= Algebraický súčet komponentov X a a aplikovaných síl

θX= uhol, ktorý tvorí výslednú silu FR S osou X

Všimnite si, že sila vyplývajúca z výrazu (6) nie je zvýraznená tučným písmenom a je to preto, že vyjadruje iba číselnú hodnotu. Adresa je určená uhlom θX.

Výraz (6) je platný pre sily pôsobiace v rovnakej rovine. Keď sily konajú vo vesmíre, zohľadní sa komponent z sily, ak pracujete s obdĺžnikovými komponentmi.

Vyriešené cvičenia

1. Stanovte sily vyplývajúce z tela, ktoré podlieha nasledujúcim silám zobrazeným na obrázku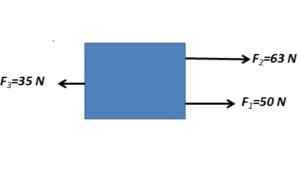

Paralelné sily sa pridávajú v rovnakom zmysle a odpočítajú sa s paralelnou silou v opačnom smere

FR= 63 n + 50 n - 35 n = 78n

Výsledná sila má veľkosť 78 N s horizontálnym smerom.

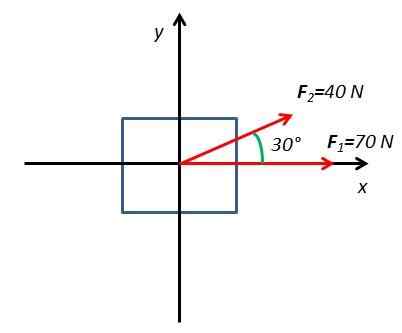
2.Vypočítajte silu vyplývajúcu z tela pod vplyvom dvoch síl F1 a F2. Sila F1 Má veľkosť 70n a aplikuje sa vodorovne. Sila F2 Má veľkosť 40 N a používa sa pod uhlom 30 ° vzhľadom na horizontálnu rovinu.

Na vyriešenie tohto cvičenia sa nakreslí voľný diagram tela s súradnicovými osami X a a

Sú určené všetky komponenty X a a síl pôsobiacich na tele. Sila F1 Má iba vodorovnú zložku na osi X. Sila F2 Má dve komponenty F2x  a f2 a ktoré sa získavajú zo sínusových a kosínových funkcií uhla 30.

Môže vám slúžiť: Trenie: Typy, koeficient, výpočet, cvičenia

F1x = F1=70n

F2x = F2 Cos 30 ° = 40 N.Cos 30 ° = 34,64n

F1y = 0

F2 a= F2 bez 30 ° = 40 bez 30 ° = 20n

∑ fX =70n+34,64n = 104,64n

∑ fa=20n+0 = 20n

Akonáhle sú stanovené výsledné sily na osi X a a Získa sa numerická hodnota výslednej sily.

FR2= (∑ fX)2+(∑ fa)2

Výsledná sila je štvorcovým koreňom letného súčtu komponentov síl

FR= √ (104,64n)2+(20n)2

FR= 106,53n

Uhol, ktorý tvorí výslednú silu FR Získava sa z nasledujúceho výrazu:

θX= opálenie-1(∑ fa / ∑ fX)

θX= tak-1(20n / 104 64n) = 10,82 °

Výsledná sila FR Má veľkosť 106,53N a má smer stanovený uhlom 10,82 °, ktorý sa tvorí s horizontálnym.

Odkazy

  1. Dola, G, Duffy, M a Percival,. Fyzika. Španielsko: Heinemann, 2003.
  2. Avison, J H. Svet fyziky. India: Thomas Nelson a Sons, 1989.
  3. Pinsent, m. Fyzický proces. Spojené kráľovstvo: Nelson Thomas, 2002.
  4. Yadav, s k. Inžinierska mechanika. Dillí: Discovery Publishing House, 2006.
  5. Serway, R A a Jewett, J W. Fyzika pre vedcov a inžinierov. Kalifornia, USA: Brooks/Cole, 2010.