Povrchové a hmotnostné sily šmykovej sily

Ten Počuť silu Je to zložená sila, ktorá sa vyznačuje rovnobežnou s povrchom, ktorý je vyvíjaný a má tendenciu rozdeliť telo, čím sa navzájom posúvajú sekcie, ktoré sú výsledkom rezu.

Schematicky je znázornená na obrázku 1, ktorý ukazuje šmykovú silu aplikovanú na dva rôzne body drevenej ceruzky. Šmyková sila zase vyžaduje dve rovnobežné a opačné sily, ktoré sú v závislosti od ich intenzity schopné deformovať ceruzku alebo ju určite zlomiť.

postava 1. Aplikovaná šmyková sila rukami spôsobuje rozpad ceruzky. Zdroj: Pixabay.

Takže aj keď hovoríte o singulárnej počutej sile, skutočne sa uplatňujú dva sily, pretože šmyková sila je a zložená sila. Tieto sily pozostávajú z dvoch síl (alebo viac v zložitých prípadoch) aplikovaných v rôznych bodoch objektu.

Dve sily rovnakej veľkosti a opačného smeru, ale s paralelnými líniami pôsobenia, predstavujú a sily. Páry neposkytujú preklad do objektov, pretože ich výsledok je neplatný, ale poskytujú čistý krútiaci moment.

S párom sa otáčajú predmety, ako je volant vozidla, alebo sa môžu deformovať a rozbiť, ako v prípade ceruzky a dreveného stola znázornené na obrázku 2.

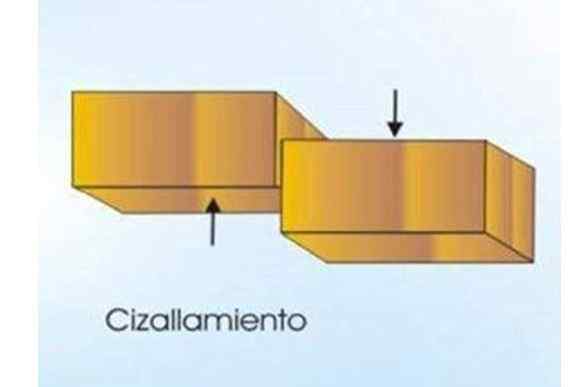Obrázok 2. Šmyková sila rozdeľuje drevenú tyč do dvoch častí. Všimnite si, že sily sú tangenciálne pre prierez Madero. Zdroj: f. Zapata.

[TOC]

Povrchové sily a hromadné sily

Zložené sily sú súčasťou hovorov povrchové sily, Presne preto, že sa aplikujú na povrch tela a nijako nesúvisia s ich hmotnosťou. Na objasnenie bodu porovnajme tieto dve sily, ktoré často pôsobia na objekty: hmotnosť a trecia sila.

Môže vám slúžiť: Graff Van Generátor: strany, ako to funguje, aplikácie

Veľkosť hmotnosti je p = mg a ako závisí od tela tela, nejde o povrchovú silu. Je to a Hromadná sila, A hmotnosť je najreferickejším príkladom.

Trenie však závisí od povahy kontaktných povrchov a nie od hmotnosti tela, na ktorom pôsobí, a preto je dobrým príkladom povrchových síl častého vzhľadu.

Jednoduché sily a kompozitné sily

Povrchné sily môžu byť jednoduchý ani zloženia. Už sme videli príklad sily zloženej v šmykovej sile, a na druhej strane je trenie predstavované ako jednoduchá sila, pretože jedna šípka je dostatočná na to, aby ju reprezentovala v telesnej schéme izolovanej z objektu.

Jednoduché sily sú zodpovedné za tlač zmien v pohybe tela, napríklad vieme, že kinetická trenie sily medzi pohybujúcim sa objektom a povrchom, na ktorom sa pohybuje, vedie k zníženiu rýchlosti.

Naopak, kompozitné sily majú tendenciu deformovať telá a v prípade šmyku alebo nožníc, konečný výsledok môže byť rez. Ostatné povrchové sily, ako je napätie alebo kompresia, predlžujú alebo stlačia telo, na ktorom konajú.

Zakaždým, keď je paradajka narezaná na prípravu omáčky alebo nožnice do časti a použije sa papier, opísané princípy sa použijú. Rezacie nástroje majú zvyčajne dva ostré kovové listy na nanesenie šmykovej sily na prierez objektu na nasekanie.

Môže vám slúžiť: Aký je magnetický moment? Obrázok 3. Šmyková sila v akcii: Jedna zo síl je aplikovaná listom noža, druhá je normálny vyvíjaný sekajúcou stolom. Zdroj: Fotografická fotografia vytvorená Katemangostar - Freepik.je

Počuť stres

Účinky šmykovej sily závisia od rozsahu sily a oblasti, na ktorej pôsobí, takže pri inžinierstve koncepcie Počuť stres, ktorá zohľadňuje silu aj oblasť.

Toto úsilie má iné významy, ako napríklad strih o Snaha o rezanie av občianskych stavbách je mimoriadne dôležitá.

Jeho užitočnosť sa okamžite chápe, keď vezmeme do úvahy nasledujúcu situáciu: Predpokladajme, že existujú dva tyče rovnakého materiálu, ale odlišná hrúbka, ktoré sú vystavené zvyšujúcim sa silám, kým ich nerozbijú.

Je zrejmé, že na prelomenie najhrubšej lišty musíte uplatniť väčšiu silu, ale úsilie je rovnaké pre každú čiaru, ktorá má rovnaké zloženie. Eseje, ako je tento, sú časté v strojárstve, vzhľadom na dôležitosť výberu vhodného materiálu pre predpokladanú štruktúru, ktorá bude optimálne fungovať.

Úsilie

Matematicky, ak označujete šmykové úsilie ako τ, Do veľkosti sily aplikovanej ako F a oblasti, na ktorej pôsobí ako A, máte priemerné šmykové úsilie:

τ_priemer= F /a

Keďže je kvocientom medzi silou a oblasťou, jednota úsilia v medzinárodnom systéme je Newton/M², nazývané Pascal a skrátene ako PA. V anglickom systéme sa používa libra/noha ² a librová sila /palec².

Môže vám slúžiť: Riešenie teplo: Ako sa vypočítava, aplikácie a cvičenia

Avšak v mnohých prípadoch je objekt pod šmykom deformy a potom obnoví svoju pôvodnú formu bez toho, aby sa rozbilo, keď sa úsilie prestane konať. Predpokladajme, že deformácia pozostáva z zmeny dĺžky.

V tomto prípade sú úsilie a deformácia úmerné, preto je možné zvýšiť nasledujúce:

Strih ∝ Unitárna deformácia

Symbol ∝ Znamená to „úmerné“ a ako pre jednotnú deformáciu, je definovaná ako pomer medzi zmenou dĺžky, ktorá sa bude nazývať AL a pôvodnou dĺžkou nazývanou L_ani. Tadiaľto:

τ ∝ (ΔL / l_ani)

Šmykový modul

Keďže je pomer medzi dvoma dĺžkami, unitárna deformácia nemá jednotky, ale pri umiestňovaní rovnakého symbolu im musí konštanta proporcionality poskytnúť. Volanie G na konštantu:

τ = G (δL / l_ani)

G sa volá Počuť modul o Strih. Má v medzinárodnom systéme Passionfly jednotky a jeho hodnota závisí od povahy materiálu. Je možné určiť takéto hodnoty v laboratóriu a nacvičovať pôsobenie rôznych síl na rôzne vzorky zloženia.

Ak je potrebné určiť veľkosť šmykovej sily z predchádzajúcej rovnice, stačí nahradiť definíciu úsilia:

τ = F /a = g (δL / l_ani)

A jasné:

F = a × g (δL / l_ani)

Rezacie sily sú veľmi časté a ich účinky sa musia brať do úvahy v mnohých aspektoch vedy a techniky. V konštrukciách sa objavujú na podporných miestach lúčov, môžu vzniknúť počas nehody a prelomiť kosť a jej prítomnosť je schopná zmeniť prevádzku strojov.

Pôsobia vo veľkom meradle na zemskej kôre, ktorá spôsobuje zlomeniny v geologických horninách a nehodách vďaka tektonickej aktivite. Preto sú tiež zodpovední za neustále modelovanie planéty.

Odkazy

1. Pivo, f. 2010. Mechanika materiálov. 5. Vydanie. McGraw Hill. 7 - 9.
2. Fitzgerald, 1996. Mechanika materiálov. Alfa omega. 21-23.
3. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6^tónth  Edimatizovať. Sála. 238-242.
4. Hibbeler, R.C. 2006. Mechanika materiálov. 6. Vydanie. Pearson Vzdelanie. 22 -25
5. Valera Negrete, J. 2005. Všeobecné fyzikálne poznámky. Žobrák. 87-98.
6. Wikipedia. Šmykové napätie. Získané z: v.Wikipedia.orgán.