Všeobecné kvadratické rovnice, príklady, cvičenia

Ten Všeobecný vzorec, ktorý je tiež známy ako rozpúšťadlo V niektorých textoch sa používa na riešenie rovníc druhého stupňa: sekera² + BX + C = 0.

V nich do, b a c Sú to skutočné čísla, s podmienkou, ktorá do sa líši od 0, bytosť X Neznámy. Potom všeobecný vzorec predstavuje klírens neznámeho výrazu, ktorý zahŕňa hodnoty do, b a c nasledovne:

postava 1. Všeobecný vzorec matematiky sa používa na riešenie kvadratických rovníc. Zdroj: f. Zapata.

A prostredníctvom tohto vzorca nájdete riešenie akéhokoľvek druhého stupňa alebo kvadratickej rovnice za predpokladu, že existuje uvedené riešenie.

Podľa historikov bola všeobecná receptúra ​​už známa starovekám babylonská matematika. Následne sa prenášal do iných národov, ako sú Egypťania a Gréci, prostredníctvom kultúrnych výmen.

Vzorec a jej varianty prišli do Európy vďaka moslimským matematikom usadeným na Pyrenejskom polostrove. Nepoužili však algebraický zápis, ktorý v súčasnosti používame. Tento zápis je spôsobený francúzskym matematikom a kryptografickým odborníkom na 16. storočie Francois Viete.

[TOC]

Kvadratické rovnice podľa všeobecného vzorca

Pozrime sa, ako vzniká všeobecný vzorec, aby ste overili jeho platnosť. Počnúc všeobecnou kvadratickou rovnicou:

sekera² + BX + C = 0

Poďme do praxe nejaké jednoduché algebraické manipulácie, aby sme dosiahli povolenie neznámeho. Existuje niekoľko spôsobov, ako to niesť, napríklad dokončenie štvorcov, ako je znázornené.

Demonštrácia všeobecného vzorca

Začneme pridaním (-C) na oboch stranách rovnosti:

sekera² + Bx = - c

A teraz sa vynásobí 4A, vždy na oboch stranách rovnosti, aby sa nezmenil výraz:

4² X² + 4ab x = - 4ac

Pridanie b²:

4²⋅x² + 4AB⋅x + B² = - 4ac + b²

Účelom je dokončiť štvorce na ľavej strane rovnosti, ktorá obsahuje neznáme, týmto spôsobom je uľahčená jeho vôľa. Teda:

Môže vám slúžiť: DETIVORY 8: Čo sú a ľahké vysvetlenie

-Prvý termín: 4² X² Je to perfektný štvorec 2AX

-Posledný, čo je B², Je to perfektný štvorec B.

-A centrálny termín je dvojitým produktom 2AX a B: 2H2AXH = 4ABX

Preto máme štvorcový binomén:

4²⋅x² + 4AB⋅x + B² = (2ax + b)²

A môžeme napísať:

(2ax + b)² = - 4ac + b²

Sme jeden krok od vyčistenia neznámeho X:

A už získame všeobecný vzorec, ktorý poznáme:

Existujú aj iné spôsoby, ako algebraicky manipulovať s kvadratickou rovnicou a získať rovnaký výsledok.

Príklady použitia všeobecného vzorca

Aby sa uplatňoval všeobecný vzorec, hodnoty A, B a C sú starostlivo určené a nahradené vo vzorci. Všimnite si symbol viacmenej v čitateľovi; To naznačuje, že musíme zvážiť dve možnosti týkajúce sa operácie, jedna so znakom + a jedna so znakom -.

Kvadratická rovnica môže mať nasledujúce riešenia podľa hodnoty sub-radikálneho množstva, známa ako diskriminácia:

-Áno b² - 4AC> 0, kvadratická rovnica má dve skutočné a rôzne riešenia.

-Kedy b² - 4AC = 0, rovnica má jedinečné riešenie, ktoré je dané:

x = -b/2a

-Nakoniec, ak b² - 4AC < 0, la ecuación no tiene soluciones reales, pero sí tiene soluciones complejas.

Pozrime sa na niektoré príklady, v ktorých sa uplatňuje všeobecný vzorec, všimnite si, že ak sa niektorý z koeficientov, ktoré sprevádzajú neznáme, neobjaví, chápe, že stojí za to 1. A ak je nezávislý termín ten, ktorý sa nenájde, potom stojí za 0.

- Príklad 1

Vyriešiť nasledujúce kvadratické rovnice:

a) 6x² + 11x -10 = 0

b) 3x² -5x -1 = 0

Odpovedať

Píšeme koeficienty každého pojmu: a = 6, b = 11, c = -10 a nahradia hodnoty vo všeobecnom vzore:

Môže vám slúžiť: zdaňovanie

x = (-11 ± 19) /12

Výsledok vedie k nasledujúcim dvom skutočným riešeniam:

X₁ = (-11 + 19)/12 = 8/12 = 2/3

X₂ = (-11 -19)/12 = -5/2

Odpoveď B

Opäť sú stanovené koeficienty: a = 3, b = -5 a c = -1. Nahradením vo vzorci:

Na rozdiel od predchádzajúceho prípadu nie je druhá druhá koreň 37 celé číslo, ale môžeme tiež zvýšiť tieto dve riešenia a nechať koreň alebo nájsť zodpovedajúcu desatinnú hodnotu pomocou kalkulačky:

X₁ = (-5 + √37)/6 ≈ 0.18

X₂ = (-5 - √37)/6 ≈ - 1.85

- Príklad 2

Vyriešte rovnicu druhého stupňa x² - 4x +13 = 0.

Odpoveď

Ako vždy, identifikujeme hodnoty koeficientov a nahradíme všeobecný vzorec: A = 1, B = - 4, C = 13. To vedie k:

Máme negatívny koreň, preto sú riešenia tejto rovnice zložité čísla. Koreň je možné vyjadriť z hľadiska Jo, ten Imaginárna jednotka:

√ (36i²) = 6i

Odkedy som² = -1, preto komplexné riešenia sú:

X₁ = (4 + 6i)/2 = 2 + 3i

X₂ = (4 - 6i)/2 = 2 - 3i

Cvičenie

10 m dlhé schodisko spočíva na zvislej stene, s nohou 6 m od tejto steny. Schodisko sa skĺzne a noha je oddelená o 3 m od základne.

Nájdite vertikálnu vzdialenosť, ktorá prechádza hornou časťou schodiska.

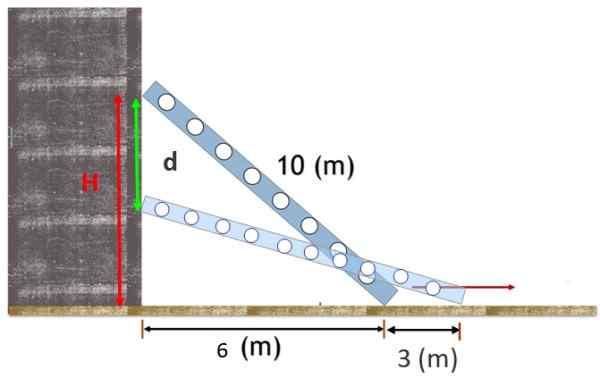Obrázok 2. Schodisko podopreté na stene trochu skĺzne a horná zastávka sa pohybuje vertikálne nadol dolu d. Zdroj: f. Zapata.

Riešenie

Ak chcete nájsť vertikálnu vzdialenosť, ktorá posúva hornú časť schodiska, musíte nájsť pozíciu, v ktorej sa pôvodne týkala zeme. Môžeme to urobiť s vetou Pythagory, pretože formovaná postava je obrázkom pravého trojuholníka:

H = (10² - 6²) ^½ = 8 m

Akonáhle sa schodisko skĺzne, vzdialenosť sa pohybuje d, Zmerajte sa, pretože vrchol bol 8 m vysoký, až kým nedosiahol svoju novú polohu, na (H-d) metre nad zemou. Neznámy na vyčistenie je D.

Môže vám slúžiť: akumulovaná frekvencia: vzorec, výpočet, distribúcia, príklady

Aby sme to našli, navrhujeme nový obdĺžnikový trojuholník, ktorý sa vytvorí po tom, čo rebrík trochu skĺzol. Tento trojuholník má stále hypotenusu rovná 10 ma a paralelný kateto je teraz 6m + 3 m = 9 m, preto:

(H-d)² = 10² - 9² = 100 - 81 = 19

Nahrádzame H = 8 m, predtým vypočítané:

(8-D)² = 19

Rovnicu je možné vyriešiť niekoľkými spôsobmi, vrátane použitia všeobecného vzorca, ktorý uvedieme nižšie s týmito krokmi:

Krok 1

Rozvíjajte pozoruhodnú ľavicu zľava:

64 -16d + D² = 19

Krok 2

Stanovte rovnicu druhého stupňa pre neznáme D:

d² - 16d + 45 = 0

Krok 3

-Koeficienty sú: a = 1, b = -16 a c = 45, nahradíme ich vo všeobecnom vzore:

Riešenia rovnice sú:

d₁ = (16 + √76)/2 ≈ 12.36 m

d₂ = (16 - √76)/2 ≈ 3.64 m

Krok 4

Získané riešenia sa analyzujú: prvý nemá fyzický zmysel, pretože nie je možné, aby rebrík zostavil 12.36 m, ak bola pôvodne zastávka 8 m vysoká na zemi.

Preto správnou odpoveďou je druhé riešenie: horná časť schodiska skĺzne d = 3.64 m.

Môže čitateľ vyriešiť problém použitím inej metódy?

Odkazy

1. Plechovka. 1977. Elementárna algebra. Venezuelské kultúrne vydania.
2. Hoffman, J. Výber matematických problémov. Zväzok 2.
3. Jiménez, r. 2008. Algebra. Sála.
4. Stewart, J. 2006. Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.
5. Zill, D. 1984. Algebra a trigonometria. McGraw Hill.