Frakcie rovnajúce sa 2/3

Ten zlomky rovnajúce sa ⅔ (Čítajú sa dve tretiny) sú tí, ktorých hodnota, vyjadrená desatinným spôsobom, je rovnaká, ktorá sa získa vydelením 2 po 3: 0.6666… Pozastavené body naznačujú, že 6 sa javí ako nekonečné časy v tejto divízii.

Frakcia ekvivalentná 2/3 je frakcia 4/6, ako sa ukázalo, že po vyriešení rozdelenia medzi 4 a 6 výslovne, desatinné 0,6666 .. . Potom je možné povedať, že 4/6 = 2/3 = 0,6666 .. .

Frakcie 2/3 a 4/6 sú ekvivalentné, pretože vydelením počtu čitateľa menovateľom sa uvádza rovnaké číslo novín 0,66666 .. . (Zdroj: f. Zapata)

Frakcia, ako už názov napovedá, je časťou alebo časťou jednotky. Frakcia ⅔ sa získa rozdelením jednotky na tri rovnaké časti a vezme dve z týchto častí.

Každá frakcia pozostáva z hornej časti, ktorá sa volá čitateľ, oddelené od dna alebo menovateľ, Cez zlomkovú čiaru. Menovateľ naznačuje, koľko častí je jednotka rozdelená a čitateľ naznačuje, koľko z týchto strán je potrebné vziať do úvahy.

Teraz zvážte frakciu 4/6 (prečítajte si šiesty). Je dokázané, že táto frakcia je rovnocenná s ⅔, pretože na rozdelenie jednotky na šesť častí je potrebné dodržiavať tieto kroky:

1. Rozdeľte jednotku na tri rovnaké časti.
2. A potom rozdeľte každú z týchto častí na polovicu a získajte celkovo šesť rovnakých častí.

Ak sú zoskupené 4 časti 1/6 jednotky, získaná suma je zlomok rovnakej hodnoty, ku ktorej sa získajú 2 časti 1/3 jednotky. V nasledujúcom grafe sa vykonáva opísaný postup: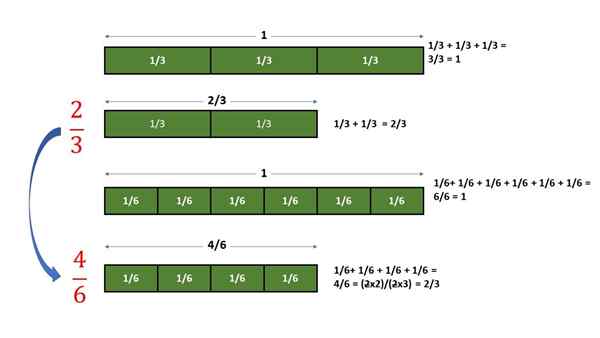

Grafické overenie, že frakcia 2/3 je rovnocenná s zlomkom 4/6. Zdroj: f. Zapata.

Môže vám slúžiť: numerické analógie: typy, aplikácie a cvičenia

Metódy na nájdenie rovnocenných frakcií

Všimnite si, že ekvivalentná frakcia 4/6 sa dá získať z 2/3 vynásobením čitateľom a menovateľom menovaného menovaného.

Keď súčasne vynásobte čitateľa a menovateľa frakcie rovnakým číslom, získa sa ekvivalentná frakcia.

Ďalším spôsobom, ako nájsť frakciu ekvivalentnú inej, by bolo rozdelenie čitateľa a menovateľa v rovnakej sume za predpokladu, že čitateľ a menovateľ sú presne deliteľné tým istým číslom. Ale nie je možné dosiahnuť, delenom rovnakým celom, ekvivalentná frakcia založená na 2/3, pretože čísla 2 a 3 sú navzájom bratranci.

Keď čitateľ a menovateľ frakcie sú navzájom hlavnými číslami, hovorí sa, že frakcia je neredukovateľný. A frakcia 2/3 je dobrým príkladom tohto druhu frakcií, v skutočnosti 2/3 predstavuje súbor všetkých frakcií rovnajúcich sa 0.666 ..

Na druhej strane je frakcia 4/6 redukovateľná a rovná frakcii ⅔, pretože čitateľ 4 a menovateľ 6 sú párne čísla, ktoré sú deliteľné 2.

Takže dva spôsoby, ako získať frakcie rovnajúce sa daným, sú:

• Súčasne zosilniť čitateľ a menovateľ 
• Znížte čitateľa a menovateľ

Zosilnenie frakcií

Na získanie frakcie ekvivalentu daného, ​​čitateľ a menovateľ sa vynásobia rovnakým obrázkom. Tu je niekoľko príkladov:

Dospelo sa k záveru, že ⅔ (dve tretiny), 4/6 (štyri šiesty), 6/9 (šesť deviateho) a 8/12 (osem dvanásty) sú medzi sebou rovnocenné frakcie, ale iba ⅔ je nezvratný zlomok.

Stručne povedané, ak začnete od neredukovateľnej frakcie ⅔, spôsob, ako získať akúkoľvek inú rovnocennú frakciu, je uplatniť tento vzorec:

Môže vám slúžiť: Vyriešené faktorizačné cvičenia

S celou kontrolou.

Metóda zosilnenia na získanie rovnocenných frakcií. Zdroj: f. Zapata

Zníženie zlomkov

Je to metóda, ktorá umožňuje získanie ekvivalentnej frakcie za predpokladu, že počiatočná frakcia má čitateľa a menovateľa s jedným alebo viacerými bežnými deliteľmi.

Nie je to prípad 2/3, ktorý je, ako už bolo povedané, je neredukovateľné. Ale napríklad zlomok 60/90 (šesťdesiat deväťdesiat rokov) Sa dá zredukovať na:

• 6/9, pretože čitateľ aj menovateľ sú deliteľní medzi desiatimi.
• 30/45, pretože čitateľ a menovateľ sú deliteľné medzi dvoma.
• 20/30, pretože čitateľ a menovateľ sú deliteľní medzi tromi.
• 12/18, pretože čitateľ a menovateľ sú deliteľní medzi piatimi.

Ak chcete získať neredukovateľnú frakciu rovnocennú s originálom, potom je potrebné rozdeliť čitateľa aj menovateľa svojím maximálnym spoločným deliteľom (MCD).

Rozklad v faktoroch, ktorý má čitateľ:

60 = 2² ⋅ 3 ⋅ 5

A vykonanie rovnakého postupu v menovateľovi:

90 = 2 ⋅ 3² ⋅ 5

MCM sú bežné hlavné faktory s jeho nižším exponentom, to znamená:

MCM (60; 90) = 2 štrí 3,5 = 30

Potom 60 medzi 30 Da 2, ktoré sa umiestni do čitateľa a pri 90 medzi 30 da 3, 3 sa umiestni do menovateľa. Preto môže byť neredukovateľná frakcia 60/90 vyjadrená ako:

Spôsoby, ako zistiť, či je daná frakcia rovnocenná s 2/3

Priamym spôsobom, ako zistiť, či sú dva alebo viac frakcií rovnocenné, je vyjadriť frakcie priamo desatinným spôsobom a ak sa všetky číslice zhodujú, je isté, že frakcie sú rovnocenné. Existujú však aj ďalšie metódy použiteľné na 2/3:

Spôsob 1

Buďte frakciou x/y, chcete vedieť, či je táto frakcia rovnocenná s 2/3:

Vyšetrovacia značka je umiestnená, pretože ešte nie je známe, či hodnoty „x“ a „y“ uspokojujú rovnosť. Vedieť, že sa to znásobuje na kríži:

Môže vám slúžiť: Vzťahy proporcionality: koncept, príklady a cvičenia

3x =? 2 a

Iba keď sa rovnosť splní, existuje istota, že X/Y je zlomok ekvivalentný 2/3.

Metóda 2

Táto metóda vyžaduje určenie maximálneho spoločného deliteľa (MCD) čitateľa a menovateľa. Potom sú obidve vydelené MCD, a ak je frakcia získaná po vykonaní opísanej operácie 2/3, potom sa dá povedať, že je to frakčný ekvivalent k nemu.

Príklady

Príklad 1

Určite, či frakcia 40/60 je rovnocenná s ⅔.

Riešenie

Metódou 1:

Metóda naznačuje, že by sa mala vynásobiť na kríži:

40 x 3 =? 60 x 2

120 =? 120

Keďže je rovnosť splnená, dospelo sa k záveru, že 40/60 je rovnocenná s 2/3.

Príklad 2

Určite, či frakcia 120/180 je rovnocenná s ⅔.

Riešenie

V tomto príklade sa uplatňuje metóda 2. Prvá vec je určiť rozklad v hlavných faktoroch 120:

120 = 2³ ⋅ 3 ⋅ 5

A rozklad vo faktoroch menovateľa je:

180 = 2² ⋅ 3² ⋅ 5

Na určenie MCD sa spoločné faktory vynásobia jeho nižším exponentom:

MCD (120; 180) = 2² ⋅ 3 ⋅ 5 = 60

Tak:

120 ÷ 60 = 2

180 ÷ 60 = 3

Preto sa dospelo k záveru, že 120/180 je rovnocenné 2/3, to znamená:

Vyriešené cvičenia

Cvičenie 1

Sú frakcie 10/15 a 12/18 ekvivalent?

Riešenie

Najrýchlejší spôsob, ako ho overiť, je množiť sa na kríž, pretože to nie sú príliš veľké hodnoty:

10 x 18 =? 15 x 12

180 =? 180

Bola získaná rovnosť, potom sa dá povedať, že 10/15 = 12/18.

Cvičenie 2

Sú frakcie 8/12 a 12/20 rovnocenné s ⅔?

Riešenie

Použije sa metóda zjednodušenia, ktorá pozostáva z delenia súčasne čitateľa a menovateľa spoločnými hlavnými faktormi, až kým nedosiahne neredukovateľný výraz:

12/12 = 4/6 = ⅔, to znamená, že prvá frakcia je rovnocenná s ⅔.

Pre druhý zlomok, ktorý máte:

12/20 = 6/10 = ⅗, ale ⅗ je neredukovateľný a odlišný od ⅔, preto sa druhá frakcia nerobí ⅔.