Objemový tok

Vysvetlíme, aký objemový tok je, ako ho vypočítať a faktory, ktoré ho ovplyvňujú

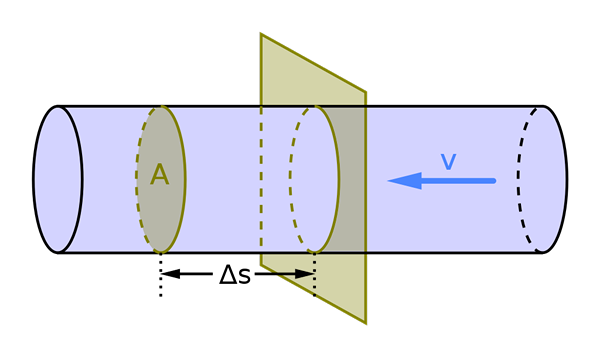
Objemový tok závisí od oblasti prierezu A a rýchlosti tekutiny v. Zdroj: Mikerun, CC BY-SA 4.0, cez Wikimedia Commons

Čo je objemový tok?

On objemový tok Umožňuje určiť objem tekutiny, ktorá prechádza prierezom potrubia a ponúka rýchlostné opatrenie, s ktorým sa tekutina pohybuje rovnakým. Preto je jej opatrenie obzvlášť zaujímavé v oblastiach, ktoré sú okrem iného aj v oblastiach rozmanitých ako priemysel, medicína, stavebníctvo a výskum.

Avšak meranie rýchlosti tekutiny (buď kvapalina, plyn alebo zmes oboch) nie je také jednoduché, ako rýchlosť posunu tuhého tela môže byť meranie. Preto sa stáva, že poznať rýchlosť tekutiny je potrebné poznať jej tok.

Z tohto a mnohých ďalších problémov týkajúcich sa tekutín, odvetvie fyziky známe ako mechanika tekutín. Prietok je definovaný ako tekutá časť potrubia prechádza, je to už potrubie, potrubie, rieka, kanál, krvný obeh atď., berúc do úvahy dočasnú jednotku.

Zvyčajne sa vypočíta objem, v ktorej sa vypočíta určitá oblasť v jednotke. Definuje sa aj tok hmotnosti alebo hmotnosti, ktorý prechádza oblasťou určenou v konkrétnom čase, hoci sa používa menej často ako objemový tok.

Ako sa vypočíta objemový tok?

Objemový tok predstavuje písmeno q. V prípadoch, keď sa tok presúva kolmo na sekciu vodiča, je určený nasledujúcim vzorcom:

Q = a = v / t

V tomto vzorci a je to časť vodiča (je to priemerná rýchlosť, ktorú má tekutina), V je objem a čas t. Pretože v medzinárodnom systéme sa oblasť alebo časť vodiča meria v M² A rýchlosť v m/s, prietok sa meria m³/s.

Môže vám slúžiť: 21 dôležitých udalostí fyziky

V prípadoch, keď rýchlosť posunu tekutiny vytvára uhol 9 s smerom kolmým na povrchovú časť A, výraz na určenie toku je nasledujúci:

Q = cos θ

To je v súlade s predchádzajúcou rovnicou, pretože keď je prietok kolmý na plochu A, 9 = 0, a preto cos θ = 1.

Vyššie uvedené rovnice sú pravdivé iba vtedy, ak je rýchlosť kvapaliny rovnomerná a ak je časť sekcie plochá. V opačnom prípade sa objemový tok počíta prostredníctvom nasledujúceho integrálu:

Q = ∫∫_siež v d s

V tomto integrálnom DS je to povrchový vektor, určený nasledujúcim výrazom:

Ds = n ds

Tam n je normálny jednotkový vektor na povrch potrubia a DS diferenciálny povrchový prvok.

Rovnica kontinuity

Charakteristiou nestlačiteľných tekutín je to, že hmotnosť tekutiny sa zachováva pomocou dvoch častí. Z tohto dôvodu je splnená rovnica kontinuity, ktorá stanovuje nasledujúci vzťah:

ρ₁ Do₁ Vložka₁ = ρ₂ Do₂ Vložka₂

V tejto rovnici ρ je hustota tekutiny.

V prípade režimov v trvalom prietoku, v ktorých je hustota konštantná, a preto je splnené, že ρ₁ = ρ₂, Zníži sa na nasledujúci výraz:

Do₁ Vložka₁ = A₂ Vložka₂

To je rovnocenné s potvrdením, že tok je zachovaný, a preto:

Otázka₁ = Q₂.

Z pozorovania vyššie z toho vyplýva, že tekutiny sa zrýchlia, keď dosiahnu užšiu časť potrubia, zatiaľ čo znižujú svoju rýchlosť, keď dosiahnu širšiu časť potrubia. Táto skutočnosť má zaujímavé praktické aplikácie, pretože umožňuje hrať s rýchlosťou posunu tekutiny.

Môže vám slúžiť: subatomické častice

Bernoulli princíp

Princíp Bernoulli určuje, že pre ideálnu tekutinu (tj tekutinu, ktorá nemá ani viskozitu alebo trenie), ktorá sa pohybuje v cirkulačnom režime cez uzavretý kanál.

Nakoniec, princíp Bernoulli nie je nič iné ako formulácia zákona o ochrane energie pre tok tekutiny. Bernoulliho rovnicu sa teda dá formulovať takto:

H +V² / 2g+p/ ρg = konštanta

V tejto rovnici h je výška a g je zrýchlenie gravitácie.

V rovnici Bernoulli sa kedykoľvek berie do úvahy energia tekutiny, energia pozostávajúca z troch komponentov.

• Kinetická zložka, ktorá obsahuje energiu, kvôli rýchlosti, s ktorou sa tekutina pohybuje.
• Zložka generovaná gravitačným potenciálom v dôsledku výšky, v ktorej sa nachádza tekutina.
• Zložka prietokovej energie, ktorá je energiou, ktorú má tekutina v dôsledku tlaku.

V tomto prípade je Bernoulliova rovnica vyjadrená takto:

H ρ g +(v² ρ)/2 + p = konštanta

Logicky, v prípade skutočnej tekutiny nie je expresia rovnice Bernoulli splnená, pretože pri vytesnení tekutiny dochádza k stratám trenia a je potrebné uchýliť sa z komplexnejšej rovnice.

Čo ovplyvňuje objemový tok?

Objemový tok bude ovplyvnený, ak dôjde k prekážke v potrubí.

Môže vám slúžiť: Light Rafrakt: prvky, zákony a experimenty

Okrem toho sa objemový prietok môže tiež meniť účinkom teploty teploty a tlaku a tlak, na ktorý je.

Jednoduchý spôsob merania objemového toku

Skutočne jednoduchá metóda na meranie objemového toku je nechať prietok tekutiny v meracej nádrži na určité časové obdobie.

Táto metóda vo všeobecnosti nie je príliš praktická, ale pravdou je, že je veľmi jednoduché a veľmi ilustratívne porozumieť významu a dôležitosti poznania toku tekutiny.

Týmto spôsobom sa tekutina nechá prúdiť do meracej nádrže po dobu, meria sa akumulovaný objem a výsledok získaný medzi uplynutým časom je rozdelený.

Odkazy

1. Prietok (tekutina) (n.d.).  Na Wikipédii. Zotavené z es.Wikipedia.orgán.
2. Objemový prietok (n.d.).  Na Wikipédii. Získaný z.Wikipedia.orgán.
3. Engineers Edge, LLC. „Rovnica prietokovej rýchlosti objemového tekutiny“. Inžinieri
4. Mott, Robert (1996). „1“. Aplikovaná kvapalina (4. vydanie). Mexiko: Pearson Education.
5. Batchelor, G.Klimatizovať. (1967). Úvod do dynamiky tekutín. Cambridge University Press.
6. Landau, L.D.; Lifshitz, e.M. (1987). Tekutina. Priebeh teoretickej fyziky (2. vydanie.). Pergamón.