Prietok elektrického poľa

Čo je tok elektrického poľa?

On prietok elektrického poľa alebo jednoducho elektrický tok je skalárne množstvo úmerné počtu elektrických polí, ktoré prechádzajú povrchom. Je označený kapitálom kapitálu Capital Letter φ (PHI).

Elektrické pole v skutočnosti „nepokúša“ tak, ako to robí prúd vody, hoci prietokové vedenia tekutiny sa podobajú líniám elektrického poľa.

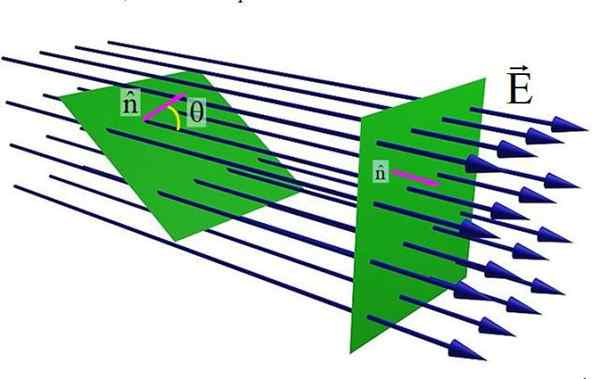
postava 1. Prietok elektrického poľa cez rovný povrch. Zdroj: Wikimedia Commons.

Horný obrázok zobrazuje rovný povrch prechádzajúci elektrickým poľom A. Keď normálny jednotkový vektor na povrch n a pole A Sú rovnobežné, množstvo poľných čiar, ktoré prechádzajú povrchom, je maximálne. Ale ako sa uhol 9 zvyšuje medzi n a A, Počet riadkov prechádzajúcich zeleným povrchom je nižší.

Na druhej strane, prietok elektrického poľa tiež závisí od rozsahu A, Pretože čím vyššie je, čím viac polí čiary prechádzajú povrchom. A samozrejme, čím väčšia je oblasť S uvedeného povrchu, tiež tok, takže je stanovená nasledujúca rovnica:

Φ = e ∙ sosθ

Tento výraz je v súlade so skalárnym produktom medzi vektormi A a n:

Φ = (A • n) S

Jednotka pre tok elektrického poľa v medzinárodnom systéme jednotiek, ak n je.m²/C (Newton X Square Metro/Coulomb). Alternatívne, keďže sa pole meria aj vo V/M (volt na metre), elektrický tok je v (v ∙ m) m).

Príklady

Podľa definície môže byť elektrický tok pozitívny, záporný alebo rovný 0. Tok elektrického poľa je:

Môže vám slúžiť: magnetizácia: orbitálny a rotátny magnetický moment, príklady

-Pozitívne, keď uhol 9 medzi A a n Je menej ako 90 °, pretože cos θ je väčší ako nula.

-Záporné, ak je tento uhol väčší ako 90 °, pretože potom je cos 9 menší ako nula.

-Prázdne, keď θ má hodnotu presne 90 °, pretože cos 90 ° = 0 a línie poľa v tomto prípade sú tangenciálne k povrchu.

-Na druhej strane, ak je uhol medzi A a n Sa rovná 0, tok získava svoju maximálnu hodnotu.

Tieto možnosti sú zobrazené na nasledujúcom obrázku:

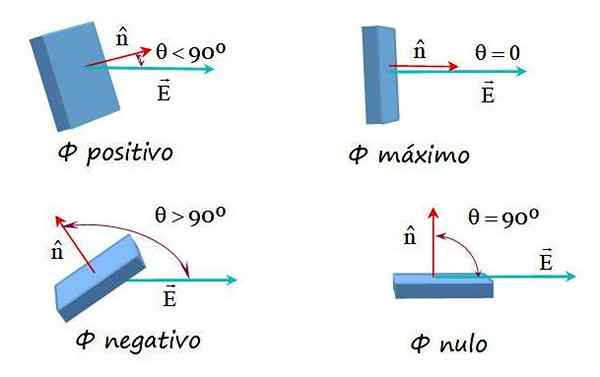Obrázok 2. Príklady prietoku elektrického poľa s rôznymi orientáciami medzi poľom a normálnym povrchovým vektorom. Zdroj: f. Zapata.

Prietok elektrického poľa na ľubovoľnom povrchu

Predtým bol prietok elektrického poľa stanovený v konkrétnom prípade rovnomerného poľa ovplyvňujúceho rovný povrch. Pre ľubovoľný povrch a/alebo nejednotné elektrické pole, uhol medzi A a n Môže sa líšiť od bodu k bodu.

Na nasledujúcom obrázku sú dva príklady, doľava zakrivený povrch a vpravo uzavretý povrch.

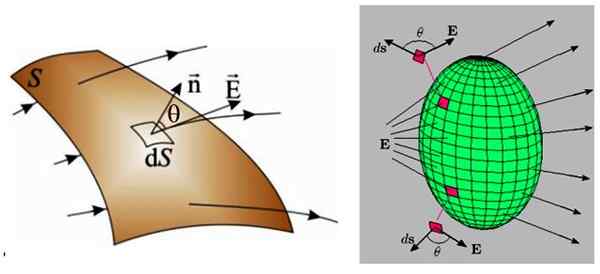Obrázok 3. Vľavo ľubovoľný povrch, cez ktorý prechádza nejednotné elektrické pole. Vpravo nejednotné elektrické pole prechádza na uzavretý povrch, preto je čistý tok v tomto prípade neplatný. Zdroj: f. Zapata.

V obidvoch prípadoch je povrch rozdelený do oveľa menších oblastí, nekonečnej veľkosti, nazývanej DS, pre ktorú tiež prechádza nekonečným tokom dφ:

dφ = (A•n) Ds = (ecosθ) ds

Celkové pole sa získa pridaním všetkých týchto nekonečných príspevkov:

Symbol S ako dolný index v integráli naznačuje, že sa musí vypočítať na celom povrchu. Ak je uzavretá, je označená malým kruhom na integráli:

Môže vám slúžiť: Antoínové konštanty: vzorce, rovnice, príklady

V prípade uzavretých povrchov, n Vždy zdôraznite, takže tok má znamenie +, keď je odchádzajúci, pretože uhol medzi A a n je menší ako 90 ° a podpíšte - keď je pole prichádzajúce, pretože potom uhol medzi A a n je väčší ako 90 ° (pozri obrázok 2).

Všimnite si, že na uzavretej ploche napravo sa počet polí čiary, ktoré vstupujú na povrch. Preto je čistý tok definovaný ako algebraický súčet prichádzajúceho toku a odchádzajúci tok, je neplatný.

Zdroj elektrického poľa v tomto prípade je mimo povrchu, čistý prietok by sa však líšil od 0, ak by zdroj elektrického poľa (distribúcia záťaže) bol vo vnútri povrchu.

Cvičenia

Cvičenie 1

Máte elektrické pole A = 3.5 kN/c X a plochý obdĺžnikový povrch 0.35 m široké od 0.7 m dlhá. Nájdite tok elektrického poľa, ktorý prechádza obdĺžnik v týchto prípadoch:

a) Povrch je rovnobežný s rovinou yz.

b) Obdĺžnik je rovnobežný s rovinou xy.

c) normálna rovina tvorí uhol 40 ° s osou x a obsahuje os a.

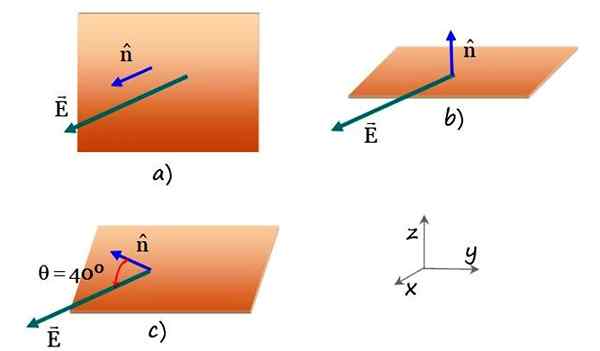Obrázok 4. Obdĺžniková rovina prechádzaná rovnomerným elektrickým poľom v rôznych orientáciách roviny. Zdroj: f. Zapata.

Roztok

Normálny vektor a vektor elektrického poľa sú rovnobežné, preto uhol 9 medzi nimi je 0 ° a elektrický tok je:

Φ = (e ∙ s) cos 0 = e ∙ s

Oblasť S obdĺžnik je:

Môže vám slúžiť: Metóda rovnobežníka: príklady, vyriešené cvičenia

S = 0.35 m x 0.7 m = 0.245 m²

Výmena v φ:

Φ = E ∙ S = 3.5 x 10³ N/C × 0.245 m² = 857.5 n ∙ m² /C.

Riešenie B

Prietok elektrického poľa je 0, pretože vektory A a n Sú kolmé na seba.

Riešenie c

Uhol 9 medzi poľom A a normálny vektor n je 40 ° (pozri obrázok), preto:

Φ = e ∙ s ∙ cos θ = 3.5 x 10³ N/C × 0.245 m² × cos 40 ° = 656.9 n ∙ m² /C.

Cvičenie 2

Vypočítajte prietok elektrického poľa, ktorý vytvára pozitívne presné zaťaženie, ktoré_ani = 2 μc umiestnený v strede polomerovej gule r = 5 cm.

Riešenie

Pole vytvorené zaťažením q_ani Nie je to jednotné, ale zo zákona Coulomb je známe, že na povrchu gule má veľkosť:

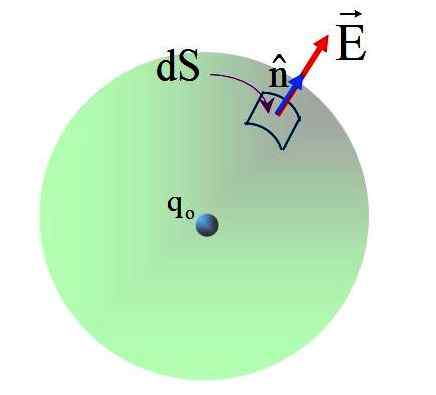Obrázok 5. Muchy poľa vyrobené na povrchu gule presným zaťažením v jeho strede. Zdroj: f. Zapata.

Pole má radiálny smer a normálny vektor n, Preto uhol medzi dvoma vektormi je 0 na všetkých bodoch sférického povrchu. Výmena:

Musíš:

Integrál DS na celom sférickom povrchu je jeho oblasť, ktorá je 4πr^2, preto:

Ktorý dospel k záveru, že prietok elektrického poľa nezávisí od povrchu S, ale od zaťaženia uzamknutého v ňom.

Jeho hodnota je:

Φ = 4π × 9 × 10⁹ x 2 × 10^-6 N⋅m²/C = 2.3 x 10⁵ N⋅m²/C

Odkazy

1. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill.
2. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 5. Elektrostatika. Editoval Douglas Figueroa (USB).
3. Giambattista, a. 2010. Fyzika. Druhý. Edimatizovať. McGraw Hill.
4. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6. Ed Prentice Hall.
5. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 1. Pearson.