Faktorovanie

Aká je faktorizácia?

Faktorizácia je metóda, prostredníctvom ktorej je polynóm vyjadrený vo forme násobenia faktorov, ktoré môžu byť čísla, písmená alebo oboje. Ak chcete zohľadniť, faktory, ktoré sú spoločné pre podmienky, sú zoskupené, a tak sa polynóm rozkladá vo viacerých polynómoch.

Ak teda faktory navzájom vynásobia, výsledkom je pôvodný polynóm. Faktorizácia je veľmi užitočná metóda, keď existujú algebraické výrazy, pretože sa môže stať znásobením niekoľkých jednoduchých pojmov; Napríklad: 2² + 2ab = 2a _* (A + b).

Existujú prípady, keď polynóm nie je možné faktorizovať, pretože medzi jeho podmienkami nie je spoločný faktor; Tieto algebraické výrazy sú teda deliteľné iba medzi sebou a 1. Napríklad: x + y + z.

V algebraickom výraze je spoločným faktorom maximálny spoločný deliteľ termínov, ktoré ho tvoria.

Metódy faktorizácie

Existuje niekoľko metód faktorizácie, ktoré sa uplatňujú v závislosti od prípadu. Niektoré z nich sú nasledujúce:

Spoločná faktorizácia

V tejto metóde sú identifikované tie bežné faktory; to znamená, že tí, ktorí sa opakujú v podmienkach výrazu. Potom sa použije distribučná vlastnosť, maximálny spoločný deliteľ je odstránený a faktorizácia je dokončená.

Inými slovami, identifikuje sa spoločný faktor výrazu a každý výraz je medzi tým rozdelený; Výsledné výrazy sa vynásobia maximálnym spoločným deliteľom, aby sa vyjadrilo faktorizáciu.

Príklad 1

Faktorizovať (B²x) + (b²a).

Riešenie

Prvým je spoločný faktor každého termínu, ktorý je v tomto prípade b², A potom sú výrazy rozdelené medzi spoločný faktor nasledovne:

(B²x) / b² = x

(B²y) / b² = y.

Faktorizácia je vyjadrená, vynásobením spoločného faktora výslednými pojmami:

(B²x) + (b²y) = b² (x + y).

Príklad 2

Faktorize (2²b³) + (3ab²).

Riešenie

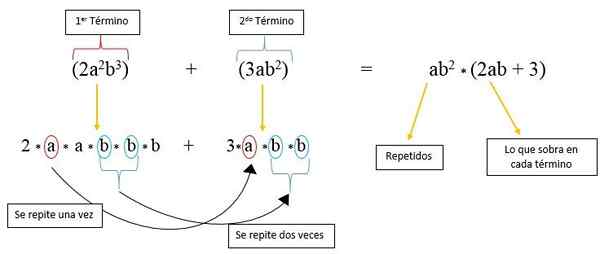
V tomto prípade máme dva faktory, ktoré sa opakujú v každom termíne, ktoré sú „a“ a „b“, a ktoré sú zvýšené k moci. Ak chcete najprv zohľadniť, dva výrazy sú rozdelené v ich dlhej podobe:

2_*do_*do_*b_*b_*B + 3A_*b_*b

Je zrejmé, že faktor „A“ sa opakuje iba raz v druhom semestri a faktor „B“ sa v tomto opakuje; Takže v prvom funkčnom období sú iba 2, faktor „A“ a jeden „B“; Zatiaľ čo v druhom funkčnom období zostáva iba 3.

Preto sa píše toľkokrát, ako „A“ a „B“ sa opakujú a vynásobia faktormi, ktoré zostávajú z každého termínu, ako je pozorované na obrázku:

Zoskupenie faktorizácie

Pretože nie vo všetkých prípadoch je maximálny spoločný deliteľ polynómu jasne vyjadrený, je potrebné urobiť ďalšie kroky, aby ste mohli prepísať polynóm, a tak faktorizovať.

Môže vám slúžiť: KONICKÉ SEKCIE: Typy, aplikácie, príklady

Jedným z týchto krokov je zoskupenie podmienok polynómu do niekoľkých skupín a potom použiť metódu spoločného faktora.

Príklad 1

Faktorizovať AC + BC + AD + BD.

Riešenie

Existujú 4 faktory, v ktorých sú dva bežné: v prvom termíne je to „C“ a v druhom je to „D“. Takto sú tieto dva výrazy zoskupené a oddelené:

(AC + BC) + (AD + BD).

Teraz je možné uplatniť metódu spoločného faktora, rozdeliť každý termín svojím spoločným faktorom a potom vynásobiť tento spoločný faktor výslednými výrazmi, ako je tento:

(Ac + bc) / c = a + b

(ad + bd) / d = a + b

C (a + b) + d (a + b).

Teraz sa získa binomén, ktorý je spoločný pre oba výrazy. Na jeho faktory sa vynásobí zostávajúcimi faktormi; Týmto spôsobom musíte:

AC + BC + AD + BD =  (C + D) _* (A + b).

Inšpekčná faktorizácia

Táto metóda sa používa na faktory kvadratických polynómov, ktoré sa tiež nazývajú trinomialy; to znamená, že tie, ktoré sú štruktúrované ako sekera² ± bx + c, kde hodnota „a“ sa líši od 1. Táto metóda sa používa aj vtedy, keď má Trinomial tvar X² ± bx + c a hodnota „a“ = 1.

Príklad 1

Faktor X² + 5x + 6.

Riešenie

Máte kvadratický trinomiál formy X² ± BX + C. Na to, aby sa najprv zohľadnilo, je potrebné zistiť, že pri násobení vedie k hodnote „C“ (tj 6) a že jej súčet sa rovná koefickejšej energii „B“. Tieto čísla sú 2 a 3:

2 _* 3 = 6

2 + 3 = 5.

Týmto spôsobom je výraz zjednodušený takto:

(X² + 2x) + (3x + 6)

Každý výraz je faktor:

• Pre (x² + 2x) Bežný termín sa odstráni: x (x + 2)
• Pre (3x + 6) = 3 (x + 2)

Výraz zostáva:

x (x +2) +3 (x +2).

Keďže máte spoločný binomický, na zníženie výrazu, vynásobí to zvyškami a musí:

X² + 5x + 6 = (x + 2) _* (x + 3).

Príklad 2

Faktorizovať 4A² + 12A +9 = 0.

Riešenie

Máte kvadratický trinomén formulára sekera² ± bx + c a na jeho faktor vynásobí všetok expresiu koeficientom x²; V tomto prípade 4.

4² + 12A +9 = 0

4² (4) + 12a (4) + 9 (4) = 0 (4)

16 a² + 12A (4) + 36 = 0

4² do² + 12A (4) + 36 = 0

Teraz je potrebné zistiť dve čísla, že keď sa navzájom vynásobia, vedie k hodnote „c“ (čo je 36) a že pri vstupe do koeficientu pojmu „a“, čo je 6.

6 _* 6 = 36

6 + 6 = 12.

Týmto spôsobom je výraz prepísaný, berúc do úvahy 4² do² = 4a _* 4. Preto sa na každý termín uplatňuje distribučná vlastnosť:

Môže vám slúžiť: Mackinder Box

(4a + 6) _* (4a + 6).

Nakoniec je výraz rozdelený koeficientom a²; to znamená, 4:

(4a + 6) _* (4a + 6) / 4 = ((4a + 6) / 2) _* ((4a + 6)/ 2).

Výraz je nasledujúci:

4² + 12a +9 = (2a +3) _* (2a + 3).

Faktorizácia pozoruhodnými výrobkami

Existujú prípady, keď, na úplné zohľadnenie polynómov predchádzajúcimi metódami, stáva sa veľmi dlhým procesom.

Preto je možné expresiu vyvinúť s vzorcami pozoruhodných produktov, a tak sa proces stáva jednoduchším. Medzi najpoužívanejšie významné výrobky patria:

• Rozdiel dvoch štvorcov: (a² - b²) = (a - b) _* (A + b)
• Dokonalý štvorec sumy: a² + 2ab +b² = (a + b)²
• Dokonalý štvorec rozdielu: a² - 2ab + b² = (a - b)²
• Rozdiel dvoch kociek: a³ - b³ = (a-b)_*(² + AB + B²)
• Súčet dvoch kociek: a³ - b³ = (a + b) _* (² - AB + B²)

Príklad 1

Faktorizovať (5² - X²)

Riešenie

V tomto prípade existuje rozdiel dvoch štvorcov; Preto sa používa vzorec pozoruhodného produktu:

(² - b²) = (a - b) _* (A + b)

(5² - X²) = (5 - x) _* (5 + x)

Príklad 2

Faktorizovať 16x² + 40x + 25²

Riešenie

V tomto prípade existuje dokonalý štvorec sumy, pretože je možné identifikovať dva štvorcové výrazy a termín, ktorý ponechal.

do² + 2ab +b² = (a + b)²

Ak chcete zohľadniť, vypočítajú sa iba odmocniny prvého a tretieho termínu:

√ (16x²) = 4x

√ (25²) = 5.

Potom sú dva výsledné výrazy vyjadrené oddelené znakom operácie a všetok štvorcový polynóm je zvýšený:

16x² + 40x + 25² = (4x + 5)².

Príklad 3

Faktorizovať 27a³ - b³

Riešenie

Expresia predstavuje odčítanie, v ktorom sú dva faktory zvýšené na kocku. Na ich zvolanie sa používa vzorec pozoruhodného produktu rozdielu v kocky, čo je:

do³ - b³ = (a-b)_*(² + AB + B²)

Na faktor sa teda kubický koreň odstraňuje z každého termínu binomického a vynásobený štvorcom prvého termínu plus produkt prvého v druhom termíne plus druhý termín na druhý termín na druhom termíne.

27a³ - b³

³√ (27a³) = 3a

„(-B³) = -B

27a³ - b³ = (3a - b) _* [(3a)² + 3ab + b²)]

27a³ - b³ = (3a - b) _* (9a² + 3ab + b²)

Faktorizácia pravidlom Ruffini

Táto metóda sa používa, keď máte polynóm stupňa väčší ako dva, aby ste zjednodušili expresiu na niekoľko menších polynómov.

Príklad 1

Faktorice q (x) = x⁴ - 9x² + 4x + 12

Riešenie

Po prvé, hľadajú sa čísla, ktoré sú deliteľmi 12, čo je nezávislý pojem; Sú ± 1, ± 2, ± 3, ± 4, ± 6 a ± 12.

Môže vám slúžiť: násobky 2: Čo sú a vysvetlenie

Potom je X nahradený týmito hodnotami, od najmenšieho po najväčší, a preto je určený, s ktorými hodnotami bude presné rozdelenie; To znamená, že zvyšok musí byť 0:

x = -1

Q (-1) = (-1)⁴ - 9 (-1)² + 4 (-1) + 12 = 0.

x = 1

Q (1) = 1⁴ - 9 (1)² + 4 (1) + 12 = 8 ≠ 0.

x = 2

Q (2) = 2⁴ - 9 (2)² + 4 (2) + 12 = 0.

A tak ďalej pre každého deliteľa. V tomto prípade sú zistené faktory pre x = -1 a x = 2.

Metóda Ruffini sa teraz používa, podľa ktorej budú koeficienty expresie vydelené faktormi nachádzajúcimi sa tak, že rozdelenie je presné. Polynomické výrazy sú usporiadané od väčšieho po nižší exponent; V prípade, že pojem chýba s stupňom, ktorý nasleduje v sekvencii, sa 0 umiestni na miesto.

Koeficienty sa nachádzajú v schéme, ako je vidieť na nasledujúcom obrázku.

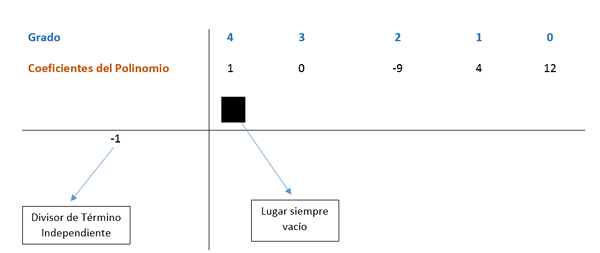
Prvý koeficient je znížený a vynásobený deliteľom. V tomto prípade je prvý deliteľ -1 a výsledok je umiestnený v nasledujúcom stĺpci. Potom sa hodnota koeficientu s získaným výsledkom pridá vertikálne a výsledok je umiestnený pod. Týmto spôsobom sa proces opakuje až do posledného stĺpca.

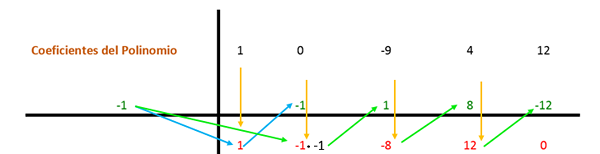
Potom sa rovnaký postup opakuje znova, ale s druhým deliteľom (ktorý je 2), pretože výraz možno stále zjednodušiť.

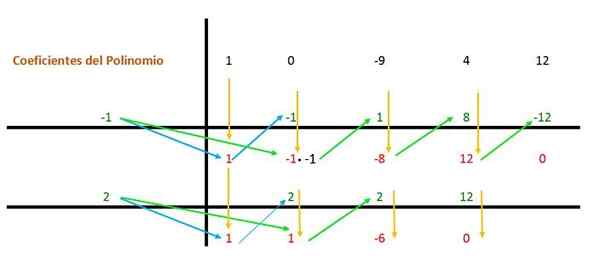
Pre každý koreň teda dosiahol polynóm termín (x - a), kde „a“ je hodnota koreňa:

(x - (-1)) _* (x - 2) = (x + 1) _* (x - 2)

Na druhej strane, tieto výrazy by sa mali vynásobiť zvyškom, ktoré zostali z pravidla Ruffini 1: 1 a -6, čo sú faktory, ktoré predstavujú stupeň. Týmto spôsobom je výraz formulára: (x² + X - 6).

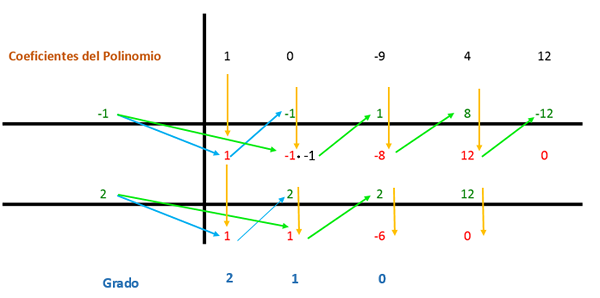
Získanie výsledku polynómovej faktorizácie metódou Ruffini je:

X⁴ - 9x² + 4x + 12 = (x + 1) _* (x - 2) _* (X² + X - 6)

Nakoniec, polynóm stupňa 2, ktorý sa objaví v predchádzajúcom expresii, možno prepísať ako (x+3) (x-2). Preto je konečná faktorizácia:

X⁴ - 9x² + 4x + 12 = (x + 1) _* (x - 2)_*(x+3)_*(X-2).

Odkazy

1. Arthur Goodman, L. H. (Devätnásť deväťdesiat šiestich). Algebra a trigonometria s analytickou geometriou. Pearson Vzdelanie.
2. J, v. (2014). Ako učiť deti o faktorovaní polynómu.
3. Manuel Morillo, a. Siež. (s.F.). Základná matematika s aplikáciami.
4. Roelse, P. L. (1997). Lineárne metódy pre polynomiálnu faktorizáciu nad konečnými oblasťami: teória a implementácie. Univerzita Essen.
5. Sharpe, D. (1987). Prstene a faktorizácia.