Bežné charakteristiky faktorov, príklady, cvičenia

On spoločný faktor algebraického výrazu je suma, ktorá je prítomná vo všetkých podmienkach. Ak je známy spoločný faktor, je možné napísať výraz rovnocenným spôsobom prostredníctvom produktu faktorov.

Nie všetky algebraické výrazy majú spoločný faktor, existujú iba tie, ktoré je možné rozdeliť iba medzi ne a 1, preto ich nie je možné písať ako produkt faktorov. Príklad expresie, ktorý nemá spoločný faktor, je:

x + y

postava 1. Spoločný faktor algebraického expresie z neho robí uvedený produkt dvoch faktorov. Zdroj: Pixabay.

Namiesto toho toto áno:

5a + 10b

Je zrejmé, že 5 je prítomné oboma výrazmi, pretože 10 = 5 ∙ 2. Pretože 5 je spoločným faktorom, potom je možné napísať nasledujúce:

5a + 10b = 5 ∙ (a + 2b)

Čitateľ môže skontrolovať prostredníctvom distribučnej vlastnosti, že výraz napravo sa rovná originálu.

Spoločným faktorom môže byť tiež doslovný alebo kombinácia čísel a písmen, napríklad v 4x² - 2x. Ten X a 2 Sú medzi faktormi a výraz zostáva ako produkt:

4x² -2x = 2x⋅ (x -1)

Výhodou nájdenia spoločného faktora výrazu a jeho písania ako produktu je to, že s ním je takmer vždy ľahké fungovať. Preto sa používa v mnohých algebraických a výpočtových postupoch, ako napríklad:

-Pri riešení rovníc, ktorých roztoky sa rýchlo odhaľujú, keď sa nachádza spoločný faktor.

-Pri výpočte limitu s neurčitosťou to môže zmiznúť správnym faktoringom.

-Vhodná faktorizácia tiež uľahčuje operácie s racionálnymi algebraickými výrazmi, ako sú sumy a odpočítanie.

[TOC]

Bežné charakteristiky faktorov

Hlavné charakteristiky spoločného faktora sú nasledujúce:

-Môže to byť číslo, algebraický výraz alebo kombinácia oboch.

-Spoločný faktor musí byť obsiahnutý v každom z výrazov expresie na faktor.

Môže vám slúžiť: Transcendentné funkcie: typy, definícia, vlastnosti, príklady

-Podľa množstva výrazov, ktoré obsahuje, to môže byť prípad:

1. Bežný monomický faktor, ak je spoločný faktor jediný termín,
2. Spoločný binomický faktor, ak máte dva termíny a
3. Bežný polynomický faktor, ak spoločný faktor pozostáva z niekoľkých termínov.

Ako nájsť spoločný faktor algebraického výrazu?

Ak chcete nájsť spoločný faktor prítomný v polynóme, musíte vypočítať maximálny spoločný deliteľ alebo MCD numerických koeficientov všetkých výrazov, ako aj písmen alebo literály každého pojmu a zvoliť silu s najmenším exponentom.

Listy alebo literály môžu byť prezentované ako monomiály, binomiály alebo polynómy, ako bude vidieť v nasledujúcich príkladoch.

Najviac sa odporúča porozumieť procesu získania spoločného faktora, je dodržiavať príklady a prax riešiť niekoľko cvičení v každom prípade.

Príklady spoločného faktora

Nesmieme strácať zo zreteľa skutočnosť, že cieľ spoločného faktora je prevedený výraz na uvedený produkt faktorov. Potom sa analyzujú najrelevantnejšie prípady:

Bežný monomický faktor

Máte nasledujúce monomialy (jednoznačné algebraické výrazy):

2x²; 10x⁴a 100x⁶a²

Čo môže byť spoločným faktorom pre tri?

Počnúc numerickými koeficientmi: 2, 10 a 100, všetky sú párne a ich MCD je 2. Pokiaľ ide o doslovnú časť, premenná X je prítomná v troch termínoch a najnižšia sila je x², Potom je spoločným faktorom 2x².

Tri navrhované výrazy môžu byť napísané ako produkty tohto faktora týmto spôsobom:

2x²= 2x²∙ 1

10x⁴y = 2x² ∙ 5x²a

100x⁶a²= 2x²∙ 50x⁴a²

Vynásobenie faktorov napravo je možné overiť, či sa získa termín ľavice.

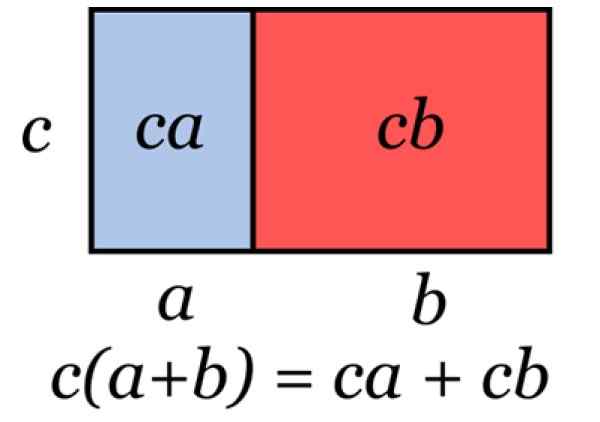Obrázok 2. Ilustrácia, ktorá predstavuje spoločný faktor. Zdroj: Wikimedia Commons.

Táto technika sa používa, keď je potrebná na zohľadnenie algebraického expresie, ako v nasledujúcich príkladoch:

• Príklad 1

Skutočnosť nasledujúci výraz:

Môže vám slúžiť: Isosceles trojuholník

5x³a + 10x²a² + 5xy²

MCD numerických koeficientov každého termínu je:

MCD (5.10) = 5

Pokiaľ ide o doslovnú časť, obidve X ako a Sú prítomné v týchto troch termínoch a najmenší exponent každého z nich je 1, preto je spoločným faktorom 5xy A môžete napísať:

5x³a + 10x²a² + 5xy²= 5xy ∙ (x² +2xy²+a)

Bežný polynomický faktor

Spoločný faktor môže pozostávať z binomického, trinomiálneho alebo všeobecného v polynóme. V takom prípade sú pokyny v predchádzajúcej časti stále platné a vyberú sa ako spoločný faktor, ktorý má najmenší exponent.

• Príklad 2

Napíšte nasledujúci výraz ako produkt dvoch faktorov:

2a (x - 1) - 3b (x -1)

Priamou kontrolou je spoločným faktorom binomický (X-1), tak:

2a (x - 1) - 3b (x - 1) = (x -1) ∙ (2a - 3b)

Faktorizácia zoskupením výrazov

Existencia spoločného faktora niekedy nie je zrejmá, ale odhaľuje sa, či sú podmienky zoskupené pohodlným spôsobom:

• Príklad 3

Faktorizovať 3x³ - 9ax² - x + 3a

Na prvý pohľad neexistuje žiadny spoločný faktor v týchto štyroch výrazoch, pretože napríklad X Je prítomný v prvých troch, ale nie v poslednom. A do Je to v druhom a v poslednom.

Pokiaľ ide o koeficienty, existujú tri termíny, v ktorých sú 3 prítomné, avšak ako spoločný faktor, malo by to byť vo všetkých podmienkach.

Zdá sa, že opísané techniky nie je možné tentoraz uplatniť. Výraz sa však môže faktorovať zoskupením prvých dvoch termínov a posledných dvoch, pričom pri umiestňovaní zátvorky je opatrný, aby znamenia sú vhodné nemeniť originál:

Môže vám slúžiť: obdĺžnikové komponenty vektora (s cvičeniami)

3x³ - 9ax² - x + 3a = (3x³ - 9ax²) - (x - 3a)

Všimnite si negatívne znamenie uprostred zátvoriek: je to potrebné, pretože inak by sa pôvodný výraz zmenil.

V ľavej zátvorke je spoločný faktor 3x², preto:

(3x³ - 9ax²) - (x - 3a) = 3x²⋅ (x - 3a) - (x - 3a)

A pozoruje sa, že sa už objavil spoločný faktor: (x - 3a), To znamená, že je to druhýkrát na získanie:

3x² (X- 3a) - (x - 3a) = (x - 3a) ∙ ( 3x²- 1)

Cvičenie spoločného faktora

Cvičenie 1

Vyriešiť 4x rovnicu³ +7x²  +6x = 0

Riešenie

„X“ je preto spoločným faktorom:

3x³ −5x²  +2x = x (3x² −5x +2) = 0

Pre výraz vľavo je 0, stačí, aby bola splnená jedna z týchto dvoch podmienok:

x = 0

Buď:

3x² −5x +2 = 0

Jedná sa o úplnú rovnicu druhého stupňa, ktorú je možné vyriešiť použitím všeobecného vzorca, tiež použitím vedeckej kalkulačky alebo inej algebraickej metódy. Riešenia tejto rovnice sú:

x = 1

x = 2/3

Po nájdení je ilustratívne písať rovnicu ako produkt 3 faktorov, hoci vyhlásenie o ňu nepožiadalo. Bolo by to takto:

x⋅ (x-1) ⋅ (x-2/3) = 0

Cvičenie 2

Vypočítajte nasledujúci limit, ak existuje:

Riešenie

Najprv sa nahradí pri x = −2, aby sa pokúsil vyhodnotiť limit, a to sa získa:

Keďže ide o neurčitosť formulára 0/0, musíte byť faktorom, aby ste sa pokúsili ho odstrániť. Menovateľ nemôže byť faktor, ale čitateľ.

V čitateľovi je spoločný faktor X:

X²+2x = x ∙ (x+2)

Faktorizovaný výraz sa nahradí v limite, a takto neurčitosť zmizne:

Dospelo sa k záveru, že limit existuje a má hodnotu −2.

Odkazy

1. Baldor, a. 2005. Algebra. Kultúrna vlastná skupina.
2. Jiménez, r. 2008. Algebra. Sála.
3. Larson, R. 2012. Predbežné vyfarbenie. 8. Vydanie. Učenie sa.
4. Stewart, J. 2007. Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.
5. Zill, D. 1984. Algebra a trigonometria. McGraw Hill.