Vyhodnotenie funkcií

Na vyhodnotenie funkcie, ktorej je diagram známy, pre určitú hodnotu alebo prvok počiatočnej sady je dosť na pozorovanie zodpovedajúceho prvku v množine príchodu. Zdroj: f. Zapata.

Aké je hodnotenie funkcií?

Ten Vyhodnotenie funkcií Spočíva v určovaní obrazu určitej hodnoty domény. Inými slovami, pre danú hodnotu počiatočnej sady musíte nájsť jej zodpovedajúcu v súprave príchodu.

Funkciu môže byť reprezentovaná niekoľkými spôsobmi. Ak je napríklad Venn Diagram k dispozícii, hodnotenie je veľmi jednoduché, stačí na výber prvku štartovacej alebo doménovej sady a pozrite si prvok, ktorý zodpovedá množine príchodu.

V časti „…… je kapitálové diagramy…“, ktorý je uvedený vyššie, pri hodnotení tejto funkcie v prvku „Kanada“ je to prvok „Ottawa“ v prípade, že to urobí s „Mexikom“, je to „Mexico City“ a tak.

Ak je funkcia daná vo forme uprataných párov, hodnotenie je tiež jednoduché: druhým členom riadného krútiaceho momentu je obraz prvého člena. Napríklad s funkciou F (x) opísanou:

f (x) = (0,0); (1.2); (2,4); (3,6); (4.8); (5.10); (6,12)

Pri hodnotení funkcie pre hodnotu 3 je výsledok 6; Pri hodnotení 5 je to 10 a tak ďalej.

Podobne je možné hodnotiť funkciu, keď je k dispozícii graf, za predpokladu, že hodnota, ktorú chcete vyhodnotiť, sa objaví v ňom.

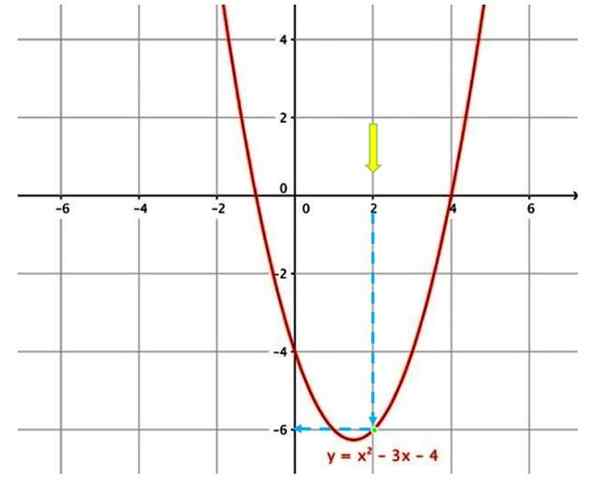Graf na vyhodnotenie funkcie

Napríklad na vyhodnotenie vyššie uvedenej funkcie, pri x = 2, je prvá vec lokalizovať v grafe x = 2 (žltá šípka).

Potom sa musíte presunúť po modrej vertikálnej šípke, až kým sa nedotknete krivky (zelený bod). Postupujte znova modrou šípkou, ktorá označuje zodpovedajúcu hodnotu na vertikálnej osi, a preto sa získa pri hodnotení funkcie pri x = 2, y = −6.

Môže vám slúžiť: trigonometrické funkcie: Základné, v karteziánskej rovine, príklady, cvičenie

Vyhodnotiť danú funkciu v matematickom zápise

V spodnej časti vyššie uvedeného grafu sa objaví grafická funkcia, ale uvedená v matematickej notácii, to znamená prostredníctvom vzorca:

f (x) = x² - 3x - 4

Ak chcete vyhodnotiť funkciu v akejkoľvek hodnote x = a, musíte nájsť f (a), ktorý sa jednoducho číta „f of a“.

Na nájdenie výsledku sa X = A vymení vo vzorci funkcie a požadované operácie a výpočty sa vykonávajú tam.

Predpokladajme, že chcete vyhodnotiť funkciu príkladu pri x = −1. To znamená, že F (−1) je potrebné nájsť.

Prvým krokom je nahradenie x = -1 vo funkcii:

f (−1) = (−1)² - 3 ∙ (−1) - 4

A potom vykonajte uvedené operácie, ktoré sú v tomto príklade:

• Nájdite štvorec −1: (−1)² = 1
• Odpočítajte predchádzajúcu hodnotu produktu 3 ∙ (−1): 3 ∙ (−1) = −3
• Z predchádzajúceho výsledku odpočítajte 4

f (−1) = (−1)² - 3 ∙ (−1) - 4 = 1 + 3 - 4 = 0

Čitateľ môže tento výsledok potvrdiť z grafu funkcie.

Opísaný postup sa môže použiť na vyhodnotenie funkcie v akejkoľvek inej hodnote domény. Napríklad nájdete F (-2), F (100) alebo dokonca F (h), kde H je ľubovoľná premenná hodnota, ktorá patrí do domény funkcie.

Vyhodnotiť funkciu pri hodnote x = h 

Predpokladajme, že chcete vyhodnotiť funkciu v určitej ľubovoľnej hodnote, častej operácii v matematickom výpočte.

V tomto prípade je X nahradený H, rovnakým spôsobom, aký sa vykonáva, keď X má akúkoľvek číselnú hodnotu a výsledok sa čo najviac zjednodušuje.

Ak výsledná operácia už nie je možné zjednodušiť, výsledná operácia zostane.

Môže vám slúžiť: ENEGON: Vlastnosti, ako vyrobiť engon, príklady

Príklad

Chcete vyhodnotiť funkciu f (x) = x² - 3x - 4 pri x = h+1. Potrebný prístup je nasledujúci:

f (H+1) = (H+1)² - 3 ∙ (H+1) - 4

Vpravo na rovnosť je prvým termínom pozoruhodný produkt:

(H+1)² = h² +2h + 1

Nasledujúci výraz sa vyrieši prostredníctvom distribučnej vlastnosti:

3 ∙ (H + 1) = 3H + 3

Pri výmene všetkých vyššie uvedených má:

f (H+1) = (H+1)² - 3 ∙ (h+1) - 4 = h² +2H + 1 - (3H + 3) - 4

Podobné výrazy sú znížené algebraickým súčtom:

f (h+1) = h² + 2H + 1 - 3H - 3 - 4 = h² - H - 6

Diferenciálny kvocient

Diferenciálny kvocient alebo pomer rozdielov d funkcie f (x) je definovaný ako:

S podmienkou H ≠ 0, čo je potrebné, pretože delenie 0 nie je definované.

Tento kvocient sa interpretuje geometricky ako sklon sekundovej čiary k krivke, to znamená čiara, ktorá prechádza dvoma jeho bodmi. Súradnice týchto bodov sú: [x, f (x)] a [x+h; f (x+h)], ako je vidieť na nasledujúcom obrázku:

Diferenciálny kvocient je rovnocenný s výpočtom sklonu sekundovej čiary k krivke, ktorá prechádza uvedenými bodmi. Zdroj: Wikimedia Commons.

Z tohto dôvodu sa tento kvocient objavuje pri výpočte derivátu funkcie, pretože „H“ priblíži hodnotu 0, sekundárna čiara má tendenciu stať sa dotyčnou čiarou v bode (x, y), pretože body v priesečníku križovatky číslo sú tak blízko, že majú tendenciu k rovnakému bodu.

Čiara sa teda stáva tangens (zachytáva krivku v jednom bode).

Toto je presne definícia odvodenej z funkcie: sklon čiary dotýkal krivky v súradnicovom bode (x, f (x))))))))))))))))).

Môže vám slúžiť: vážené médiá: Ako sa vypočítajú, príklady a cvičenia

Ako je vidieť, diferenciálny kvocient vyžaduje vyhodnotenie funkcie v (x + h) a v x. Nasledujúce príklady ilustrujú, ako to urobiť.

Príklad 1

Chcete nájsť diferenciálny kvocient funkcie f (x) = 2x - 3. Prvým krokom je zvýšenie vyhodnotenia funkcie pre x = x + h, ako je tento:

f (x+h) = 2 ∙ (x+h) - 3 = 2x+2h - 3

Potom sa výsledok nahradí v definícii d, uvedenej predtým:

S H ≠ 0.

Čitateľ je v takom prípade zjednodušený, čím sa znižuje podobné výrazy:

Nakoniec sú spoločné faktory v čitateľovi a menovateľovi zjednodušené:

D = 2

Príklad 2

Nájdite diferenciálny kvocient funkcie f (x) = x² - 3x - 4.

Postupujeme ako v predchádzajúcom príklade, nájdenie prvého F (x+h), nahradenie výsledku v D a zjednodušenie maxima:

f (x+h) = (x+h)² - 3 (x+h) - 4 = x² + 2HX + H² - 3x - 3H - 4

= 2x+h-3

Preto:

D = 2x+H-3

Kde h ≠ 0.

Vyriešené cvičenia

Cvičenie 1

Vyhodnotiť funkciu f (x) = 2x² - 4x + 1 Kedy:

a) x = -1
b) x = 0
c) x = 2

Roztok

F (-1) = 2 (-1)² - 4 (-1) + 1 = 2 + 4 + 1 = 7

Riešenie B

f (0) = 2 (0)² - 4 (0) + 1 = 0 - 0 + 1 = 1

Riešenie c

f (2) = 2 ∙ 2² - 4 ∙ 2 + 1 = 8 - 8 + 1 = 1

Cvičenie 2

Tím ochrany prírody zistil, že funkcia w (t) = 0.lt² + 1.8T slúži na modelovanie množstva odpadu „W“ v kilogramoch, ktoré sú hodené do určitej rieky v čase „t“, ktoré je uvedené v dňoch.

Vypočítajte množstvo odpadu hodeného do rieky na konci:

a) 3 dni
b) 1 týždeň
c) 1 mesiac

Roztok

W (t) Funkcia sa hodnotí v t = 3 dni:

W (3) = 0.1 × 3² +1.8 × 3 = 0.9 + 5.4 = 6.3 kilogramy

Riešenie B

Pred vyhodnotením musíte stráviť 1 týždeň až dni:

1 týždeň = 7 dní

W (7) = 0.1 × 7² +1.8 × 7 = 4.9 + 12.6 = 17.5 kilogramov

Riešenie c

Opäť je potrebné transformovať mesiace na dni:

1 mesiac = 30 dní

W (30) = 0.1 × 30² +1.8 × 30 = 90 + 54 = 144 kilogramov

Odkazy

1. Larson, R. 2012. Predbežné vyfarbenie. 8. Vydanie. Učenie sa.
2. Inštitút Monterey. Hodnotenie funkcií. Získané z: Montereyinstitute.orgán.
3. Stewart, J. 2007. Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.
4. Sullivan, m. 1997. Predbežné vyfarbenie. 4. Vydanie. Pearson Vzdelanie.
5. Zill, D. 2008. Predbežné náskoky s výpočtovými pokrokmi. 4. Vydanie. McGraw Hill.