Stanovenie translačnej rovnováhy, aplikácie, príklady

On Prekladacia rovnováha Je to stav, v ktorom je objekt ako celok, keď sú kompenzované všetky sily pôsobiace. Matematicky je to rovnocenné s tým, že f₁+ F₂ +  F₃ +.. . = 0, byť f₁, F₂,  F₃... zapojené sily.

Skutočnosť, že telo je v translačnej rovnováhe, neznamená, že je nevyhnutne v pokoji. Toto je konkrétny prípad predchádzajúcej definície. Objekt môže byť v pohybe, ale pri absencii zrýchlenia to bude jednotný priamy pohyb.

postava 1. Prekladová rovnováha je dôležitá pre veľké množstvo športov. Zdroj: Pixabay.

Takže ak je telo v pokoji, pokračuje. A ak už máte pohyb, bude mať konštantnú rýchlosť. Všeobecne platí, že pohyb akéhokoľvek objektu je zložením prekladov a rotácií. Preklady môžu byť znázornené na obrázku 2: lineárne alebo zakrivené.

Ale ak je jeden z bodov objektu pevne stanovený, potom je jedinou možnosťou pohybu otáčanie. Príkladom je CD, ktorého centrum je opravené. CD má možnosť otáčať sa okolo osi, ktorá prechádza týmto bodom, ale nie pohybovať sa.

Ak majú objekty pevné body alebo sú podporované na povrchoch, hovorí sa o tom odkazy. Odkazy interagujú obmedzujúce pohyby, ktoré je objekt schopný urobiť.

[TOC]

Stanovenie translačnej rovnováhy

Pre rovnováhu s časticami je platné, aby ste sa uistili, že:

F_R = 0

Alebo súhrnný zápis:

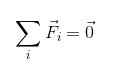
Je zrejmé, že na to, aby telo bolo v translačnej rovnováhe, sily, ktoré na ňom konajú, musia byť nejakým spôsobom kompenzované, aby jeho výsledok bol neplatný.

Týmto spôsobom sa objekt nezažije zrýchlenie a všetky jeho častice sú v pokoji alebo experimentujú priame preklady s konštantnou rýchlosťou.

Môže vám slúžiť: Teória veľkého tresku: Charakteristiky, fázy, dôkazy, problémy

Teraz, ak sa objekty môžu otočiť, spravidla to urobia. Preto väčšina pohybov pozostáva z kombinácií translácie a rotácie.

Rotácia objektu

Ak je rotačná rovnováha dôležitá, môže byť potrebné zabezpečiť, aby sa objekt neotáčal. Potom musíte študovať, či na to konajú krúžky alebo momenty.

Krútiaci moment je veľkosť vektora, od ktorej závisia rotácie. Vyžaduje, aby sa uplatňovala sila, ale bod toho je tiež dôležitý. Ak chcete objasniť túto myšlienku, zvážte rozšírený predmet, v ktorom koná sila F A uvidíme, či ste schopní vytvoriť rotáciu vzhľadom na nejakú os alebo.

Je už intuitané, že stlačením objektu v bode P silou F, Je možné otočiť bod O, s anti -horlivým smerom. Ale smer, ktorým sa aplikuje sila, je tiež dôležitý. Napríklad sila aplikovaná na obrázku média nebude schopná otočiť objekt, hoci ho určite môže presunúť.

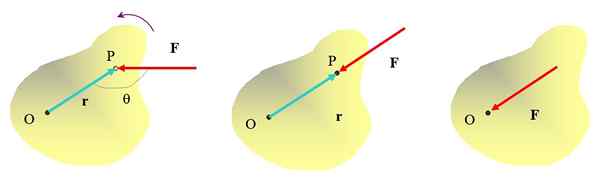Obrázok 2. Rôzne spôsoby, ako aplikovať silu na rozsiahly predmet, iba na obrázku extrémnej ľavej ľavej strane sa získa rotačný efekt. Zdroj: Self Made.

Aplikujte silu priamo v bode alebo sa nepoužije ani na otočenie objektu. Potom je zrejmé, že na dosiahnutie rotačného účinku sa musí sila aplikovať v určitej vzdialenosti od osi rotácie a jej konanie by nemalo prejsť touto osou.

Definícia krútiaceho momentu

Krútiaci moment alebo moment sily, označený ako τ, vektor zodpovedný za zostavenie všetkých týchto skutočností, je definovaný ako:

τ = r x f

Vektor r Je nasmerovaný z osi rotácie do bodu použitia sily a účasť uhla medzi R a F je dôležitá. Preto je veľkosť krútiaceho momentu vyjadrená ako:

Môže vám slúžiť: Newtonov prvý zákon: vzorce, experimenty a cvičenia

τ = r.F.SEN Otázka

Najúčinnejší krútiaci moment dochádza, keď r a F Sú kolmé.

Teraz, ak je potrebné, aby neexistovali žiadne rotácie alebo tieto prechody s konštantným uhlovým zrýchlením, je potrebné, aby súčet krútiacich momentov pôsobiacich na objekt bol nulová, analogická s tým, čo sa považovalo za sily:

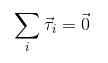
Rovnováha

Rovnováha znamená stabilitu, harmóniu a rovnováhu. Aby sa pohyb objektu vlastnil tieto charakteristiky, musia sa uplatniť podmienky opísané v predchádzajúcich oddieloch:

1) f₁+ F₂ +  F₃ +.. . = 0

2) τ₁+ τ₂ +  τ₃ +.. . = 0

Prvá podmienka zaručuje translačnú rovnováhu a druhá rotačná. Obidve sa musia splniť, ak sa chce objektom zostať v statická rovnováha (neprítomnosť pohybu akéhokoľvek druhu).

Žiadosti

Rovnovážné podmienky sú použiteľné na početné štruktúry, pretože keď sa budovy alebo rozmanité objekty vybudujú s úmyslom, že ich časti sú udržiavané v rovnakých relatívnych pozíciách navzájom. Inými slovami, že objekt nie je odzbrojený.

Je to dôležité napríklad pri výstavbe mostov, ktoré zostávajú pevné pod nohami, alebo pri navrhovaní obývateľných štruktúr, ktoré nemenia polohu alebo majú tendenciu k výpisu.

Aj keď sa predpokladá, že rovnomerný priamy pohyb je extrémne zjednodušenie pohybu, ktorý sa zvyčajne vyskytuje málo v prírode zvažuje homogénne pre životné prostredie.

V mnohých mobilných štruktúrach vyrobených človekom je dôležité, aby sa zachovala konštantná rýchlosť: napríklad na mechanických schodoch a montážnych vedeniach.

Môže vám slúžiť: Druhý zákon termodynamiky: vzorce, rovnice, príklady

Príklady translačnej rovnováhy

Toto je klasické cvičenie napätia, ktoré držia lampu v rovnováhe. Je známe, že lampa váži 15 kg. Nájdite veľkosti potrebného napätia, aby ste ho udržali v tejto polohe.

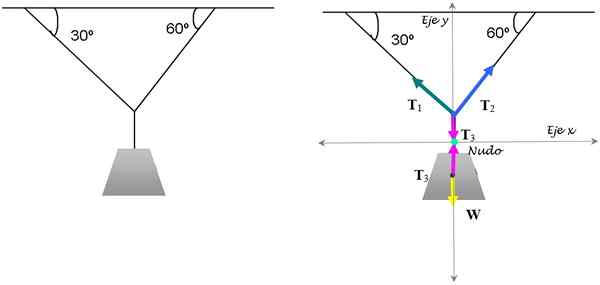Obrázok 3. Vyváženie žiarovky je zaručené uplatňovaním stavu translačnej rovnováhy. Zdroj: Self Made.

Riešenie

Aby sme to vyriešili, zameriavame sa na uzol, kde sa stretávajú tri reťazce. Príslušné diagramy voľného tela pre uzol a pre žiarovku sú znázornené na obrázku vyššie.

Hmotnosť žiarovky je W = 5 kg . 9.8 m/s² = 49 n. Aby bola lampa v rovnováhe, stačí, aby bola splnená podmienka prvého vyváženia:

Tón₃ - W = 0

Tón₃ = W = 49 n.

Napätie Tón₁ a Tón₂ Musia sa rozložiť:

Tón_1y + Tón_{2 a} - Tón₃ = 0 (Leto sily pozdĺž osi y)))

-Tón_1x +Tón_2x = 0 (Leto sily pozdĺž osi x)

Aplikácia trigonometrie:

Tón₁.Cos 60 ° +t₂ .Cos 30 ° = 49

- Tón₁.Sen60 ° +t₂.Sen30 ° = 0

Je to systém dvoch rovníc s dvoma neznámymi, ktorých odpoveď je: Tón₁ = 24.5 n a Tón₂ = 42.4 n.

Odkazy

1. Rex, a. 2011. Základy fyziky. Pearson. 76 - 90.
2. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 1. 7^mamička. Edimatizovať. Učenie sa. 120 - 124.
3. Serway, r., Vulle, C. 2011. Základy fyziky. 9^nat Edimatizovať. Učenie sa. 99-112.
4. Tippens, P. 2011. Fyzika: Koncepty a aplikácie. 7. vydanie. Kopec MacGraw. 71 - 87.
5. Walker, J. 2010. Fyzika. Addison Wesley. 332 -346.