Podmienky prekladateľstva, príklady, cvičenia

Uvádza sa, že objekt je v Preklad Keď súčet síl, ktoré na neho konajú, je nula. To neznamená, že existuje nevyhnutne zvyšok, ale pohyb, ak existuje, by bol rovnomerný alebo výlučne rotačný rektilineárny v prípade rozsiahleho objektu.

Mechanické rovnovážne podmienky sú založené na Newtonových zákonoch o mechanike. Prvý zákon nám skutočne hovorí, že predmet je v pokoji alebo sa pohybuje s rovnomerným priamym pohybom MRU, za predpokladu, že na ňu nepochopí žiadna čistá sila.

Táto lampa je v prekladovej rovnováhe

Výsledná sieťová sila alebo sila je teraz jednoducho vektorový súčet všetkých síl pôsobiacich na objekt. Podľa Newtonovho druhého zákona sa táto suma musí rovnať produktu medzi hmotnosťou a zrýchlením, ale ak objekt nie je zrýchlený, táto suma je zrušená.

A keďže neexistujú žiadne zrýchlenie, sú uvedené dve možnosti: telo je v pokoji, to znamená, že sa nepohybuje, alebo ak áno, musí to byť s MRU. V prvom prípade sa hovorí o statickej nadnárodnej rovnováhe a v druhej dynamike.

Rovnováha prekladu je dôležitým faktorom v mnohých aspektoch inžinierstva, napríklad pri výstavbe. Prvky, ktoré tvoria budovu: lúče, káble, rámy a ďalšie, musia byť v rovnováhe, aby sa zaručila stabilita krytu.

Vyváženie prekladu sa hľadá aj v mobilných štruktúrach, ako sú mechanické schody, dopravné skupiny a v praxi mnohých športov.

[TOC]

Podmienka prekladu

Predpokladajme, že niekoľko síl koná na tele, ktoré označujeme ako F₁, F₂, F₃.. . F_n, Použitie výrazného listu na zdôraznenie skutočnosti, že sily sú vektormi a musia sa ako také pridať.

Vektorový súčet všetkých týchto síl sa nazýva výsledná sila ani Čistá sila. Ak táto sumarizácia vedie k nulovému vektoru, podmienka prekladového zostatku je splnená:

Môže vám slúžiť: zatvorený elektrický obvod

F₁+ F₂+ F₃.. .+ F_n = 0

Túto podmienku je možné napísať kompaktne pomocou súčtu:

∑ F_Jo = 0

Pokiaľ ide o komponenty výslednej sily, predchádzajúca rovnica, ktorá je vektorom, môže byť rozdelená na tri skalárne rovnice, jedna pre každú zložku výslednej sily:

∑ f_Ix = 0; ∑ f_a = 0 a ∑ f_z = 0

V praxi to nie je ľahké.

To je dôvod, prečo skutočné predmety nie sú takmer nikdy oslobodené od vonkajších síl, a preto je ťažké získať rovnováhu prekladu.

Inžinieri tak používajú mechanizmy na zníženie trenia, ako sú ložiská a použitie mazivých olejov.

Diagramy bezplatného tela

Schéma voľného tela je schéma, v ktorej sú nakreslené sily, ktoré pôsobia na tele. Keď sa hľadá rovnováha prekladu, tieto sily musia byť vyvážené. Napríklad, ak pôsobíte vertikálnou silou nasmerovanou nadol, napríklad hmotnosť, musí existovať vertikálna sila, ktorá má presne rovnakú veľkosť.

Túto silu môže byť dodávaná rukou, ktorá vydrží objekt tak, aby nespadla, lano alebo jednoducho povrch stola.

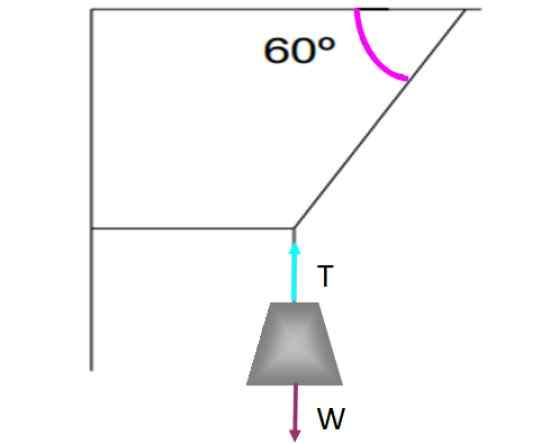
Ak na povrchu existuje tangenciálna sila, napríklad kinetické alebo statické trenie, musí existovať iná opačná sila, aby existovala rovnováha. Napríklad, pozorujme hmotnosť, ktorá visí z reťazcov znázornených na nasledujúcom obrázku.

Príklad objektu, ktorý je v translačnej rovnováhe, je to, že to váži s výhradou strechy pomocou reťazcov usporiadaných tak, ako je to znázornené na obrázku. Zdroj: f. Zapata.

Hmotnosť zostáva v rovnováhe prekladu a bez pohybu, vďaka vertikálnemu lanu, ktoré ho drží cvičením napätia Tón To kompenzuje váhu W. Každá sila bola zastúpená na západe cez šípku, každú rovnakú veľkosť a rovnakým smerom, ale opačným smerom.

Môže vám slúžiť: izobarický proces: vzorce, rovnice, experimenty, cvičenia

Vyvažovacia sila

Predpokladajme, že súbor síl pôsobí na objekt. Toto sa nazýva a sily z ktorých výsledky sa nachádzajú, ako je vysvetlené vyššie: pridanie každej zo systémových síl vektorovo.

No, silou oproti tomuto výsledku sa volá vyváženosť. Ak je výsledná sila F_R A vyvažovacia sila je A, tak:

A + F_R = 0

Preto:

A = - F_R

Príklady rovnováhy translácie

Mnoho objektov, ktoré nachádzame denne, vo vnútri a vonku z domu, je v prekladovej rovnováhe:

Budovy a cesty

Budovy a cesty sú postavené tak, aby zostali stabilné a neotáčali sa ani sa neotáčali. Avšak v mrakodrape a vo všeobecnosti veľmi vysoké budovy je potrebná určitá flexibilita na odolávanie činom vetra.

Knihy a predmety v policiach

Knihy v knižnici a produkty v obchodoch sú objekty, ktoré zostávajú v prekladovej rovnováhe a bez pohybu.

Nábytok

Nábytok, televízor s plochou obrazovkou a obrazy na stene, ako aj žiarovky, ktoré visia zo stropu, aby sme spomenuli niektoré objekty, sú v prekladovej rovnováhe.

Semafor

Semafory sú pripevnené stĺpcami a káblami, aby nespadli. Vieme však, že vietor ich núti oscilovať.

Verejné osvetlenie

Verejné osvetľovacie svetlá sú tiež v prekladovej rovnováhe, pripevnené na svetelných príspevkoch, napríklad hlavný obraz hlavného obrázka.

Cvičenie

Aká veľkosť by mala mať silu F_siež statické trenie pre box na obrázku zostane v pokoji uprostred naklonenej roviny uhol a 37 °? Hmotnosť škatule je m = 8 kg.

Môže vám slúžiť: API Gravity: Stupnica a klasifikácia surovej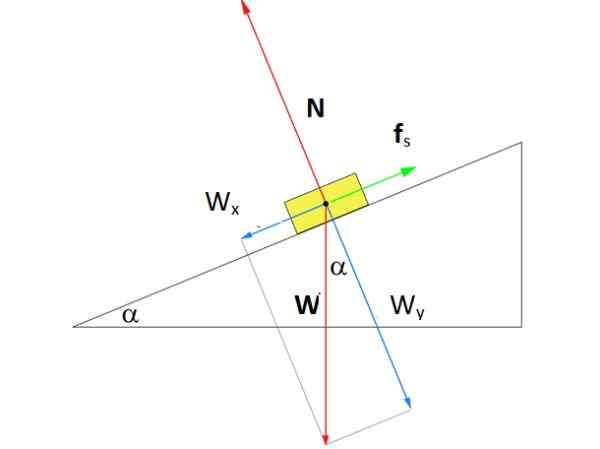Diagram voľného tela pre pokojový predmet na naklonenej rovine. Zdroj: f. Zapata.

Riešenie

Obrázok zobrazuje diagram voľného tela v rovine. Na ňu pôsobia tri sily: váha W, nasmerované vertikálne nadol, normálne N, čo je kolmá sila vyvíjaná povrchom roviny nad škatuľou a nakoniec statickou trecou silou F_siež To je proti krabici, aby skĺzol z kopca.

Stav prekladacej rovnováhy to stanovuje:

W + N + F_siež = 0

Musíte si však uvedomiť, že ide o vektorovú sumu a aby ste ju vykonali, je potrebné rozložiť sily do komponentov pozdĺž súradnicových osí.

Na obrázku bol nakreslený súradnicový systém, v ktorom os x prechádza rovnobežne s povrchom naklonenej roviny. S touto voľbou spadá statické trenie na túto os, zatiaľ čo normál je na osi a. Hmotnosť je jediná sila, ktorá je naklonená a musíme sa rozložiť pomocou trigonometrie:

W_X = W. hriech α
W_a = W. cos α

Súčet síl v každej osi je:

∑ f_a = N - w_a = 0
∑ f_X = f_siež - W_X = 0

Z tejto poslednej rovnice z toho vyplýva, že:

F_siež = W_X

A ako w_X = W. sin a a rozsah hmotnosti zase je w = m.g, keď je G hodnota gravitácie, takže veľkosť statického dotyku je jednoducho:

F_siež = mjedme gh. α = 8 kg × 9.8 m/s² × sen 37 ° = 47.2 n.

Odkazy

1. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill.
2. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 2. Dynamika. Editoval Douglas Figueroa (USB).
3. Giambattista, a. 2010. Fyzika. Druhý. Edimatizovať. McGraw Hill.
4. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 1. 7^mamička. Edimatizovať. Učenie sa.
5. Tippens, P. 2011. Fyzika: Koncepty a aplikácie. 7. vydanie. McGraw Hill.