Mechanické vzorce energie, koncept, typy, príklady, cvičenia

Ten mechanická energia objektu alebo systému je definovaný ako súčet jeho potenciálnej energie a kinetickej energie. Ako už názov napovedá, systém získava mechanickú energiu vďaka pôsobeniu mechanických síl, ako je hmotnosť a elastická sila.

Podľa množstva mechanickej energie, ktorú má telo, bude mať tiež schopnosť vykonávať mechanickú prácu.

postava 1. Pohyb horských automobilov je možné opísať zachovaním mechanickej energie. Zdroj: Pixabay.

Energia - typ, ktorý je - je skalárne množstvo, a preto chýba smer a význam. Byť A_m Mechanická energia objektu, Alebo jeho potenciálna energia a Klimatizovať Jeho kinetická energia, vzorec na jej výpočet je:

A_m = K + u

Jednotka v medzinárodnom energetickom systéme akéhokoľvek druhu je Joule, ktorá je skrátená ako J. 1 j je rovnocenné s 1 n.m (Newton na meter).

Pokiaľ ide o kinetickú energiu, počíta sa takto:

K = ½ m.vložka²

Kde m Je to hmotnosť objektu a vložka Jeho rýchlosť. Kinetická energia je vždy kladné množstvo, pretože hmotnosť a štvorec rýchlosti sú. Pokiaľ ide o potenciálnu energiu, ak ide o gravitačnú potenciálnu energiu, máte:

U = m.g.h

Tu m Stále je to cesto, g Je to zrýchlenie gravitácie a h Je to výška vzhľadom na referenčnú úroveň alebo ak je uprednostňovaná, zem.

Teraz, ak má príslušné telo elastickú potenciálnu energiu -môže to byť jar -je to preto, že je komprimované alebo možno predĺžené. V takom prípade je pridruženou potenciálnou energiou:

U = ½ kx²

S klimatizovať ako pružinová konštanta, ktorá naznačuje, aké ľahké alebo ťažké je ju deformovať a X Dĺžka uvedenej deformácie.

[TOC]

Koncept a vlastnosti mechanickej energie

Prehĺbenie definície uvedenej skôr, mechanická energia potom závisí od energie spojenej s pohybom tela: kinetická energia, plus príspevok potenciálnej energie, ktorá, ako sme povedali, môže byť gravitačná, kvôli hmotnosti a hmotnosti a polohy, ktorá zaberá telo rešpekt k pôde alebo referenčnej úrovni.

Uveďme to jednoduchým príkladom: Predpokladajme, že máte hrniec na podlahe a v pokoji. Pretože je to stále, nemá kinetickú energiu a je tiež na zemi, miesto, odkiaľ nemôže spadnúť; Preto nemá gravitačnú potenciálnu energiu a jej mechanická energia je 0.

Predpokladajme, že teraz niekto umiestni hrniec tesne na okraj strechy alebo okna, o 3.0 metrov vysoký. Za to musela osoba robiť prácu proti gravitácii. Pot má teraz gravitačnú potenciálnu energiu, môže spadnúť z tejto výšky a jej mechanická energia už nie je neplatná.

Obrázok 2. Hrniec na vrchu okna má gravitačnú potenciálnu energiu. Zdroj: Pixabay.

Za týchto okolností má hrniec A_m = U A toto množstvo závisí od výšky a hmotnosti hrnca, ako je uvedené predtým.

Povedzme, že hrniec padá, pretože to bolo v neistej pozícii. Keď sa jeho rýchlosť zvyšuje as ňou jej kinetická energia, zatiaľ čo energia gravitačnej potenciálu klesá, pretože stráca výšku. Mechanická energia v akomkoľvek okamihu pádu je:

Môže vám slúžiť: aké sú odvodené veľkosti?

A_m = U + k = ½ m.vložka² + m.g.h  

Konzervatívne a nekonzervatívne sily

Keď je hrniec v určitej výške, má gravitačnú potenciálnu energiu, pretože jej vyliezol, urobil prácu proti gravitácii. Rozsah tejto práce stojí za to isté ako ten, kto robí gravitáciu, keď hrniec spadnúť Z rovnakej výšky, ale má opačné znamenie, pretože bol vyrobený proti nemu.

Práca, že sily ako gravitácia a elasticita závisia iba od počiatočnej polohy a konečnej polohy získanej objektom. Bez ohľadu na to, po ktorej nasledovala trajektória, aby prešla z jedného na druhého, záleží iba na hodnotách samotných hodnôt. Sily, ktoré sa správajú týmto spôsobom Konzervatívne sily.

A keďže sú konzervatívne, umožňujú prácu, aby sa uložili ako potenciálna energia v konfigurácii objektu alebo systému. To je dôvod, prečo hrniec na okraji okna alebo strechy mal možnosť pádu a s ním vyvinúť pohyb.

Na druhej strane existujú sily, ktorých diela závisia od cesty, po ktorej nasledujú objekt, na ktorý konajú. Trenie patrí do tohto typu síl. Obojstvá sa strávia viac, keď pôjdete z jedného miesta na druhé na ceste s mnohými kolami, ako keď idete za ďalším priamym.

Trecie sily robia prácu, ktorá znižuje kinetickú energiu tela, pretože ich spomaľuje. A preto mechanická energia systémov, v ktorých má trenie, má tendenciu klesať.

Časť práce vykonanej silou sa stratí napríklad teplom alebo zvukom.

Typy mechanickej energie

Mechanická energia je, ako sme povedali, súčet kinetickej energie a potenciálnej energie. Teraz môže potenciálna energia pochádzať z rôznych konzervatívnych síl: hmotnosť, elastická pevnosť a elektrostatická sila.

- Kinetická energia

Kinetická energia je skalárne množstvo, ktoré sa vždy stáva pohybom. Akákoľvek častica alebo pohybujúci sa objekt má kinetickú energiu. Objekt, ktorý sa pohybuje v priamke, má kinetickú energiu prekladu. To isté sa stane, ak sa otáča, v tomto prípade sa hovorí o rotačnej kinetickej energii.

Napríklad auto, ktoré sa pohybuje po ceste, má kinetickú energiu. Tiež futbalový loptu, keď sa pohybuje po ihrisku alebo osobe, ktorá rýchlo kráča, aby sa dostala do kancelárie.

- Potenciálna energia

Vždy je možné priradiť skalárnu funkciu nazývanú potenciálna energia k konzervatívnej sile. Rozlišujú sa tieto:

Gravitačný potenciál

Ten, ktorý majú všetky objekty na základe svojej výšky vzhľadom na zem alebo referenčnú úroveň, ktorá bola vybraná ako taká. Ako príklad, niekto, kto je v pokoji na terase budovy 10 -kmeňov, má potenciálnu energiu 0 vzhľadom na zem terasy, ale nie vzhľadom na ulicu, ktorá je 10 poschodí pod.

Elastická potenciálna energia

Zvyčajne sa ukladá v objektoch, ako sú ligy a pramene, spojené s deformáciou, ktorú zažívajú pri ich natiahnutí alebo komprimovaní.

Elektrostatická energia

Je uložený v systéme elektrického zaťaženia v rovnováhe kvôli elektrostatickej interakcii medzi nimi. Predpokladajme, že v malej vzdialenosti existujú dve elektrické náboje toho istého samostatného znaku; Keďže sú elektrické poplatky s rovnakým znakom odrazené, očakáva sa, že externý agent vykonal prácu, aby ich priblížil.

Môže vám slúžiť: striedanie aktuálnych obvodov: typy, aplikácie, príklady

Po jeho umiestnení sa systém podarí uložiť prácu, ktorú agent konfiguroval, vo forme elektrostatickej potenciálnej energie.

Zachovanie mechanickej energie

Vracia sa do padajúceho hrnca, gravitačná potenciálna energia, ktorú mala, keď bola na okraji strechy, sa transformuje na kinetický pohyb pohybu. To sa zvyšuje na úkor prvého, ale súčet oboch zostáva konštantný, pretože pád hrnca je aktivovaný gravitáciou, čo je konzervatívna sila.

Existuje výmena medzi jedným typom energie a druhým, ale pôvodná suma je rovnaká. Preto je platné potvrdiť, že:

Počiatočná mechanická energia = konečná mechanická energia

A_{Počiatočný m} = E_{M finále}

Alternatívne:

Klimatizovať_{počiatočný} + Alebo_{počiatočný} = K _Konečný + Alebo_Konečný

Inými slovami, mechanická energia sa nemení a ∆E_m = 0. Symbol „∆“ znamená zmenu alebo rozdiel medzi konečným množstvom a počiatočným.

Na správne uplatnenie zásady ochrany mechanickej energie na riešenie problémov je potrebné:

-Platí iba vtedy, keď sú sily pôsobiace na systém konzervatívne (závažnosť, elastický a elektrostatický). V tom prípade: ∆E_m = 0.

-Študijný systém musí byť izolovaný. V žiadnom prípade nedochádza k prenosu energie.

-Ak sa objaví v probléme, potom sa objaví ∆E_m ≠ 0. Napriek tomu by sa problém mohol vyriešiť nájdením práce vykonávaných konzervatívnymi silami, pretože je príčinou zníženia mechanickej energie.

Odpočet mechanickej ochrany energie

Predpokladajme, že konzervatívna sila pôsobí na systém, ktorý vykonáva prácu W. Táto práca spôsobuje zmenu kinetickej energie:

W = ∆K (Cinetic Work-Energy Terem)

Je dôležité poznamenať, že kinetika teórie pracovnej energie je použiteľná aj v prípade nekonzervatívnych síl.

Na druhej strane je práca zodpovedná aj za zmenu potenciálnej energie a v prípade konzervatívnej sily je zmena potenciálnej energie definovaná ako negatív tejto práce:

W = -∆U

Zodpovedanie týchto rovníc, pretože obe sa vzťahujú na prácu vykonanú na objekte:

∆K = -∆U 

Klimatizovať_F - Klimatizovať_ani = -(u_F - Alebo_ani)

Predplatné symbolizujú „konečné“ a „počiatočné“. Zoskupenie:

Klimatizovať_F + Alebo_F = K_ani + Alebo_ani                                                    

Príklady mechanickej energie

Mnoho objektov má zložité pohyby, v ktorých je zložité nájsť výrazy polohy, rýchlosti a zrýchlenia ako funkciu času. V takýchto prípadoch je uplatňovanie zásady mechanickej energie.

Pozrime sa na niektoré príklady, v ktorých sa zachováva mechanická energia:

-Lyžiar, ktorý sa posúva z kopca cez zasnežené kopce, za predpokladu, že sa predpokladá neprítomnosť trenia. V tomto prípade je hmotnosť príčinná sila pohybu v celej trajektórii.

-Ruské horské vozíky, Je to jeden z najtypickejších príkladov. Hmotnosť je tiež sila, ktorá definuje pohyb a mechanickú energiu, sa zachováva, ak neexistuje trenie.

Môže vám slúžiť: ionizačná energia

-Jednoduché kyvadlo Skladá sa z hmoty, ktorá je predmetom neroztiahnuteľného lana -nemení dĺžku -ktorá sa krátko oddeľuje od vertikálu a môže sa oscilovať. Vieme, že sa nakoniec zastaví v dôsledku trenia, ale keď sa trenie nezohľadňuje, zachová sa aj mechanická energia.

-Blok, ktorý ovplyvňuje pružinu Opravené jedným koncom k stene, všetko nasadené na veľmi hladký stôl. Blok komprimuje pružinu, cestuje do určitej vzdialenosti a potom sa vystrelí v opačnom smere, pretože pružina sa tiahne. Tu blok získa svoju potenciálnu energiu vďaka práci, ktorá robí jar na ňom.

-Jar a lopta: Keď je pružina stlačená loptou, toto skákanie. Je to preto, že keď sa jar uvoľní, potenciálna energia sa stáva kinetickou energiou v lopte.

-Skok: Funguje to podobne ako jar, elasticky propaguje osobu, ktorá na neho skočí. To využíva svoju váhu pri skákaní, s ktorými deformuje trampolínu, ale táto, pri návrate do svojej pôvodnej polohy, dáva prepojke impulz.

Obrázok 3. Odrazový mostík pôsobí ako jar a propaguje ľudí, ktorí na ňu skočia. Zdroj: Pixabay.

Vyriešené cvičenia

- Cvičenie 1

Predmet hmotnosti M = 1 kg sa spadne o rampu z výšky 1 m. Ak je rampa extrémne hladká, vypočítajte rýchlosť tela, keď sa pružina zrazí.

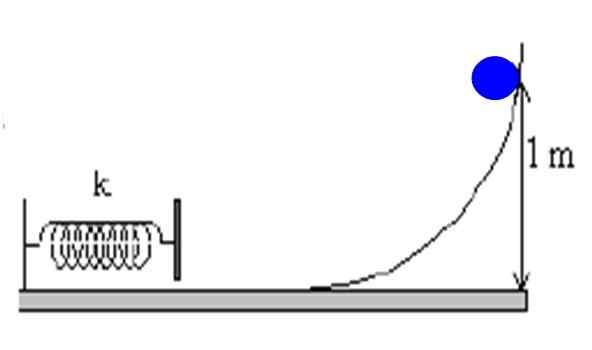Obrázok 4. Objekt zostupuje na rampe bez trenia a komprimuje pružinu, ktorá je pripevnená k stene. Zdroj: f. Zapata.

Riešenie

Vyhlásenie uvádza, že rampa je hladká, čo znamená, že jedinou silou, ktorá pôsobí na telo, je jej váha, konzervatívna sila. Je teda potrebné uplatniť ochranu mechanickej energie medzi akýmikoľvek bodmi trajektórie.

Zvážte body označené na obrázku 5: A, B a C.

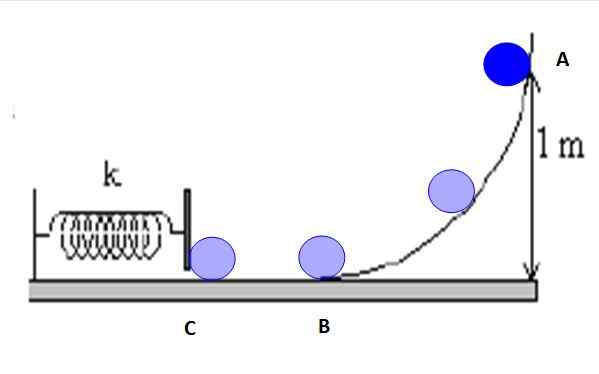Obrázok 5. Cesta, ktorá nasleduje po objekte, je trenie a mechanická energia sa zachováva medzi akýmikoľvek pármi bodov. Zdroj: f. Zapata.

Je možné stanoviť ochranu energie medzi A a B, B a C alebo C alebo ktoréhokoľvek zo stredných bodov na rampe. Napríklad medzi A a C máte:

Mechanická energia pri A = mechanická energia v C

A_mamička = E_MC

Klimatizovať_Do + Alebo_Do = K_C + Alebo_C

½ m.vložka_Do² + m.g.h_Do = ½ m v_C² + m.g.h_C

Ako sa uvoľňuje z bodu A, rýchlosť V_Do = 0, na druhej strane h_C = 0. Okrem toho sa hmotnosť zrušuje, pretože je to spoločný faktor. Tak:

g.h_Do = ½ V_C²

vložka_C²= 2 g.h_Do

- Cvičenie 2

Nájdite maximálnu kompresiu, ktorú zažije pružina cvičenia, ak je to istá elastická konštanta 200 N/m.

Riešenie

Elastická konštanta pružiny označuje silu, ktorá sa má aplikovať na deformovanie jednotky dĺžky. Pretože konštanta tejto jari má hodnotu k = 200 n/m, naznačuje to, že na stlačenie alebo natiahnutie 1 m je potrebných 200 N.

Byť X Vzdialenosť, ktorú objekt komprimuje pružinu pred zastavením v bode D:

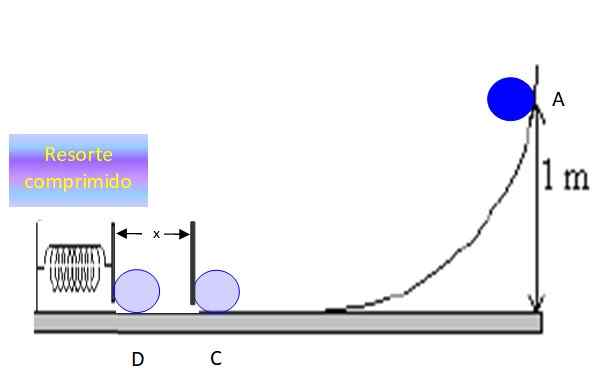Obrázok 6. Objekt komprimuje pružinu vzdialenosť x a na chvíľu sa zastaví. Zdroj: f. Zapata.

Zachovanie energie medzi bodmi C a D sa uvádza, že:

Klimatizovať_C + Alebo_C = K_D + Alebo_D

V bode C nemá gravitačnú potenciálnu energiu, pretože jej výška je 0, ale má kinetickú energiu. V D sa úplne zastavil, preto tam K_D = 0, ale namiesto toho máte k dispozícii potenciálnu energiu komprimovanej pružiny u_D.

Zachovanie mechanickej energie zostáva:

Klimatizovať_C = U_D

½ MV_C² = ½ kx²

 

Odkazy

1. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill.
2. Figueroa, D. 2005. Séria: Fyzika pre vedu a inžinierstvo. Zväzok 1. Kinematika. Editoval Douglas Figueroa (USB).
3. Rytier, r.  2017. Fyzika pre vedcov a inžinierstvo: Strategický prístup. Pearson.
4. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 1.
5. Wikipedia. Mechanická energia.Obnovené z: je.Wikipedia.orgán.