Gibbs Free Energy Units, ako sa vypočítava, vyriešené cvičenia

Ten Gibbs Free Energy (bežne nazývaná g) je termodynamický potenciál definovaný ako rozdiel v entalpie H, s výnimkou produktu teploty t, entropickými systémami systému:

G = H - T S

Gibbs Free Energy sa meria v jouloch (podľa medzinárodného systému), v Ergios (pre ligový systém jednotiek), v kalóriách alebo elektrónových voltoch (Pre elektro volty).

postava 1. Diagram ukazujúci definíciu energie Gibbs a jej vzťah s ostatnými termodynamickými potenciálmi. Zdroj: jadrová energia.slepo.

V procesoch, ktoré sa vyskytujú pri konštantnom tlaku a teplote. V takýchto procesoch (g) predstavuje energiu dostupnú v systéme, ktorá sa môže stať.

Napríklad pri exotermických chemických reakciách sa entalpia znižuje, zatiaľ čo entropia sa zvyšuje. Vo funkcii Gibbs sa tieto dva faktory pôsobia, ale iba vtedy, keď energia Gibbs zníži reakciu, k reakcii dôjde spontánne.

Takže, ak je variácia G negatívna, proces je spontánny. Keď funkcia Gibbs dosiahne svoje minimum, systém dosiahne stabilnú rovnováhu. Stručne povedané, v procese, pre ktorý tlak a teplota zostávajú konštantné, môžeme potvrdiť:

- Ak je proces spontánny, potom ΔG < 0

- Keď je systém v rovnováhe: ΔG = 0

- V nepontánnom procese sa zvyšuje: ΔG> 0.

[TOC]

Ako sa vypočítava?

Gibbs Free Energy (G) sa vypočíta podľa definície uvedenej na začiatku:

G = H - Tleks

Entalpy H je zase termodynamický potenciál definovaný ako:

H = u + p v

- Krok za krokom

Ďalej sa uskutoční analýza kroku -PEP, aby ste poznali nezávislé premenné, ktoré sú Gibbs Energy funkciou:

1- prvého zákona termodynamiky, vnútorná energia súvisí s entropickými systémami a jeho objemom V pre reverzibilné procesy prostredníctvom diferenciálneho vzťahu:

Môže vám slúžiť: etídiumbromid: Štruktúra, vlastnosti, použitie, toxicita

du = dq - dw = tds - pdv

Z tejto rovnice z toho vyplýva, že vnútorná energia U je funkciou premenných S a V:

U = u (s, v)

2- Získa sa z definície H a získanie diferenciálu:

dh = du + d (p v) = du + vdp + pdv

3- Nahradenie výrazu pre DU získané v (1) musíte:

DH = TDS - PDV + VDP + PDV = TDS + VDP

Odtiaľ sa dospelo k záveru, že entalpia H závisí od entropie a tlaku p, to znamená:

H = h (s, p)

4- Teraz sa vypočíta celkový diferenciál voľnej energie Gibbs

Dg = dh -tds -sdt = tds + vdp -tds -sdt

Kde bol DH nahradený výrazom nájdeným v (3).

5- Nakoniec, zjednodušením, že dostanete: DG = VDP - SDT, Je zrejmé, že voľná energia G závisí od tlaku a teploty t ako:

G = g (p, t)

- Maxwellove termodynamické vzťahy

Z analýzy v predchádzajúcej časti Z toho vyplýva, že vnútorná energia systému je funkciou entropie a objemu:

U = u (s, v)

Potom diferenciál Alebo byť:

du = ∂_SiežU |_Vložka DS + ∂_VložkaU |_Siež DV = TDS - PDV

Z tohto expresie v čiastočných derivátoch je možné odvodiť tzv. Termodynamické vzťahy Maxwell. Čiastočné deriváty sa uplatňujú, keď funkcia závisí od viac ako jednej premennej a ľahko sa vypočítava použitím vety nasledujúcej časti.

Maxwellov prvý vzťah

 ∂_VložkaT |_Siež = -Mone_SiežP |_Vložka 

Aby ste sa dostali k tomuto vzťahu, Clairautská veta - Schwarz o čiastočných derivátoch, ktoré uvádzajú nasledujúce:

„Zmiešané deriváty druhého poriadku s vymenenými premennými sú rovnaké za predpokladu, že funkcie, ktoré sa majú odvodiť, sú kontinuálne a diferencovateľné“.

Maxwellov druhý vzťah

Počnúc tým, čo bolo demonštrované v bode 3 predchádzajúcej časti:

Môže vám slúžiť: Faktory, ktoré ovplyvňujú rozpustnosť

H = h (s, p) a dh = tds + vdp

Možno získať:

 ∂_PT |_Siež = ∂_SiežV |_P 

Pokračujte podobným spôsobom s Gibbsovou voľnou energiou G = g (p, t) a s voľnou energiou Helmholtz F = f (t, v) Získať ďalšie dve termodynamické vzťahy Maxwella. 

Obrázok 2. Josiah Gibbs (1839-1903) bol americký fyzik, chemik a matematik, ktorý veľmi prispel k termodynamike. Zdroj: Wikimedia Commons.

Maxwellove štyri termodynamické vzťahy 

1- spojené s vnútornou energiou u: ∂_VložkaT |_Siež = -Mone_SiežP |_Vložka

2- ten získaný z entalpie H: ∂_PT |_Siež = ∂_SiežV |_P 

3- súvisiace s energiou Helmholtz F: ∂_TónP |_Vložka = ∂_VložkaS |_Tón 

4- spojené s voľnou energiou Gibbs G: ∂_TónV |_P = -Mone_PS |_Tón

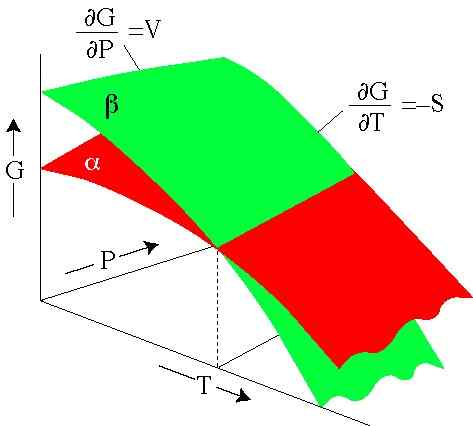Obrázok 2. Gibbsova energia závisí od tlaku a teploty. Každý povrch predstavuje fázu. (Serc.Karleton.Edu)

Vyriešené cvičenia

Cvičenie 1

Vypočítajte variáciu voľnej energie Gibbs pre 2 móly ideálneho plynu pri teplote 300 000 počas izotermálnej expanzie, ktorá vedie k počiatočnému objemu systému 20 litrov k konečnému objemu 40 litrov.

Riešenie

Zapamätať si definíciu Gibbsovej voľnej energie je:

G = H - T S

Potom bude konečná variácia f:

ΔG = ΔH - T ΔS, Pretože Δt = 0

V ideálnych plynoch Entalpia závisí iba od jej absolútnej teploty, ale keďže ide o izotermický proces, potom ΔH = 0 a ΔG = - t δs.

Pre ideálne plyny je variácia entropie izotermického procesu: 

Δs = nr ln (v₂/V₁)

To sa týkalo prípadu tohto cvičenia, ktoré máme:

ΔS = 2 mol x 8 314 j/(k mol) x ln (40L/20L) = 11,53 j/k

Potom môžeme získať zmenu v Helmholtzovej energii:

ΔG = - 300K x 11,53 j/k = -3457,70 j.

Cvičenie 2

Berúc do úvahy, že voľná energia Gibbs je funkciou teploty a tlaku g = g (t, p); Stanovte variáciu g počas procesu, v ktorom sa teplota nemení (izotermálna) pre n móly ideálneho monoatomického plynu.

Môže vám slúžiť: Stroncium Hydroxid (SR (OH) ₂)

Riešenie

Ako je uvedené vyššie, zmena energie Gibbsovcov závisí iba od zmeny teploty t a objemu V, takže jej nekonečná variácia sa vypočíta podľa:

DG = -SDT + VDP

Ale ak je to proces, v ktorom je teplota konštantná, potom DF = + VDP, takže konečná zmena tlaku ΔP vedie k zmene energie Gibbs danej:

ΔG = + ∫ vdp = + ∫ (n r t) dp/p = + n r t ln (Δp)

Použitie ideálnej plynovej rovnice:

P v = n r t

Počas izotermálneho procesu sa stáva, že:

D (p v) = p dv + v dp = 0

To je:

dp/p = - dv/v

Takže predchádzajúci výsledok je možné napísať v závislosti od variácie objemu ΔV:

ΔG = + ∫ vdp = + ∫ (n r) dp/p = - ∫ (n r t) dv/v = -n r t ln (ΔV)

Cvičenie 3

Berúc do úvahy nasledujúcu chemickú reakciu:

N₂0 (g) + (3/2) alebo₂ g) ↔No₂ (g) Pri teplote t = 298 K

Nájdite variáciu voľnej energie Gibbs a prostredníctvom získaného výsledku uveďte, či ide o spontánny proces.

Riešenie

Pod krokmi:

- Prvý krok: Reakcie Entalpies

ΔHR = 2*ΔH (nie₂ (g)) - Ah (n₂0 (g)) = 2*33,2-81,6 = -15,2 kJ/mol

- Druhý krok: variácia reakčnej entropie

ΔSr = 2*s (nie₂ g)) - S (n₂0 (g)) - (3/2) S (alebo₂ (G)) = 2*240,1 - 220,1 - 1,5*205,2 = -47,7 J/(mol*k).

- Tretí krok: Variácia vo funkcii Gibbs

Táto hodnota určí rovnováhu medzi klesajúcou energiou a zvyšujúcou sa entropiou, aby zistila, či je reakcia konečne spontánna alebo nie.

Δgr = ΔHR -t ΔSr = -15,2 -298*(-47,7) = -985,4 j/mol

Pretože ide o negatívnu variáciu energie Gibbs, je možné dospieť k záveru, že ide o spontánnu reakciu pri teplote 298 K = 25 ° C.

Odkazy

1. Castaños e. Bezplatné energetické cvičenia. Získané z: Lidiaconlachimica.Slovník.com.
2. Cengel a. 2012. Termodynamika. 7. vydanie. McGraw Hill.
3. Librettexts. Gibbs Free Energy. Získané z: Chem.Librettexts.orgán
4. Librettexts. Čo sú bezplatná energia. Získané z: Chem.Librettexts.orgán
5. Wikipedia. Gibbs Free Energy. Obnovené z: je.Wikipedia.com
6. Wikipedia. Gibbs Free Energy. Zdroj: In.Wikipedia.com