Charakteristiky kinetickej energie, typy, príklady, cvičenia

Ten Kinetická energia objektu je to, čo je spojené s jeho pohybom, takže ho nemilujúce objekty nemajú, hoci iné typy energie môžu mať. Rýchlosť hmoty aj objektu prispieva k kinetickej energii, ktorá sa v zásade vypočíta pomocou rovnice: K = ½ mv²

Kde Klimatizovať Je to kinetická energia v jouloch (energetická jednotka v medzinárodnom systéme), m Je to cesto a vložka Je to rýchlosť tela. Niekedy sa kinetická energia označuje aj ako A_c ani Tón.

postava 1. Pohybové autá majú kinetickú energiu na základe ich pohybu. Zdroj: Pixabay.

[TOC]

Charakteristiky kinetickej energie

-Kinetická energia je skalárna, preto jej hodnota nezávisí od smeru alebo zmyslu, v ktorom sa objekt pohybuje.

-Závisí to od štvorca rýchlosti, čo znamená, že duplikovaním rýchlosti sa jej kinetická energia jednoducho nedotiahne, ale zvyšuje sa 4 -krát. A ak naštartuje svoju rýchlosť, potom sa energia vynásobí deväť a tak ďalej.

-Kinetická energia je vždy pozitívna, pretože hmotnosť aj štvorec rýchlosti a faktor ½ sú.

-Objekt má kinetickú energiu alebo keď je v pokoji.

-Mnohokrát zmena V kinetickej energii objektu, ktorá môže byť negatívna. Napríklad, ak na začiatku jeho pohybu bol objekt rýchlejší a potom sa začal zastaviť, rozdiel Klimatizovať_Konečný - Klimatizovať_{počiatočný} je menej ako 0.

-Ak objekt nezmení svoju kinetickú energiu, jeho rýchlosť a jej hmotnosť zostávajú konštantné.

Chlapci

Bez ohľadu na to, aký druh pohybu má objekt, pokiaľ sa pohybuje, bude mať kinetickú energiu, či už sa prenáša pozdĺž priamky, otáča sa na kruhovej obežnej dráhe akéhokoľvek typu alebo zažije kombinovaný pohyb rotácie a prekladu.

V tomto prípade, ak je objekt modelovaný ako a častica, To znamená, že hoci má hromadnú hmotu, jeho rozmery sa nezohľadňujú, jej kinetická energia je ½ MV², Ako je uvedené na začiatku.

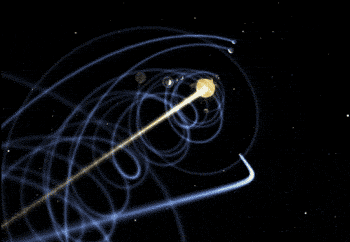
Napríklad kinetická energia Zeme vo svojom prekladateľskom pohybe okolo slnka, s vedomím, že jej hmotnosť je 6.0 · 10²⁴ kg rýchlo 3.0 · 10⁴ m/s je:

K = ½ 6.0 · 10²⁴ kg x (3.0 · 10⁴ pani)² = 2.7 · 10³³ J.

Neskôr sa ukáže viac príkladov kinetickej energie v rôznych situáciách, ale zatiaľ sa dá opýtať, čo sa stane s kinetickou energiou systému častíc, pretože skutočné objekty majú veľa veľa.

Kinetická energia systému častíc

Ak máte systém častíc, kinetická energia systému sa vypočíta pridaním príslušných kinetických energií každého z nich:

K = ½ m₁vložka₁² + ½ m₂vložka₂² + ½ m₃vložka₃² +..

Použitie sumarizácie zostáva: K = ½ ∑m_Jo vložka_Jo², kde index „i“ označuje i-tisto časticu príslušného systému, jeden z mnohých, ktorí tvoria systém.

Je potrebné poznamenať, že tento výraz je platný, či sa systém pohybuje alebo rozbije, ale v druhom prípade je možné použiť vzťah medzi lineárnou rýchlosťou vložka a uhlová rýchlosť Ω a nájdite nový výraz K:

vložka_Jo= ΩR_Jo

K = ½ ∑m_Jo(Ω_Jor_Jo)²= ½ ∑m_Jor_Jo²Ω_Jo²

V tejto rovnici, r_Jo Je to vzdialenosť medzi časticou I-éry a osou rotácie, považovaná za pevnú.

Môže vám slúžiť: červený trpaslík

Teraz predpokladajme, že uhlová rýchlosť každej z týchto častíc je rovnaká, čo sa stane, ak vzdialenosti medzi nimi zostávajú konštantné, ako aj vzdialenosť od osi rotácie. Ak áno, index „i“ nie je potrebný pre Ω A to je z tohto súčtu:

K = ½ Ω² (∑m_Jo r_Jo²)

Kinetická energia rotácie

Volanie Jo Na zhrnutie v zátvorkách sa získava táto ďalšia kompaktnejšia expresia, známa ako kinetická rotácia energie:

K = ½ iΩ²

Tu Jo získať názov moment zotrvačnosti systému častíc. Moment zotrvačnosti závisí, ako vidíme, nielen od hodnôt mas, ale aj od vzdialenosti medzi nimi a osou rotácie.

Na základe toho môže byť systém ľahšie otočiť vzhľadom na určitú os ako s ohľadom na inú. Z tohto dôvodu poznanie okamihu zotrvačnosti systému pomáha zistiť, aká bude vaša odpoveď.

Obrázok 2. Ľudia, ktorí sa točia v kolese Carousel, majú kinetickú rotáciu energie. Zdroj: Pixabay.

Príklady

Pohyb je bežný vo vesmíre, skôr je zriedkavé, že existujú odpočinkové častice. Na mikroskopickej úrovni sa hmota skladá z molekúl a atómov s určitou osobitnou dispozíciou. To však neznamená, že atómy a molekuly akejkoľvek pokojovej látky sú tiež.

V skutočnosti častice vo vnútri objektov nepretržite vibrujú. Nemusia sa nevyhnutne presúvať z jedného miesta na druhé, ale zažívajú oscilácie. Zníženie teploty ide ruka v ruke so znížením týchto vibrácií, takže absolútna nula bude rovnocenná s celkovým zastavením.

Ale absolútna nula sa doteraz nedokázala dosiahnuť, aj keď v niektorých laboratóriách s nízkymi teplotami bola veľmi blízko k jeho dosiahnutiu.

Pohyb je bežný v galaktickom meradle, ako aj v atómoch a atómových jadrách, takže rozsah kinetických energetických hodnôt je extrémne široký. Pozrime sa na niektoré číselné príklady:

-70 kg osoba, ktorá trotuje 3.50 m/s má kinetickú energiu 428.75 J

-Počas výbuchu supernovy sa emitujú častice s kinetickou energiou 10⁴⁶ J.

-Kniha, ktorá klesá z výšky 10 centimetrov, sa dostane na zem s kinetickou energiou, ktorá sa rovná 1 joule viac -menej.

-Ak sa osoba v prvom príklade rozhodne bežať rýchlosťou 8 m/s, jej kinetická energia sa zvyšuje, až kým nedosiahne 2240 j.

-Baseballová guľa Cesto 0.142 kg spustených na 35.8 km/h má kinetickú energiu 91 j.

-V priemere je kinetická energia molekuly vzduchu 6.1 x 10^{-dvadsaťjeden} J.

Obrázok 3. Výbuch supernovy v galaxii cigariet, ktorú vidí teleskop Hubble. Zdroj: NASA Goddard.

Pracovná veta - kinetická energia

Práca vykonaná silou na objekt je schopná zmeniť jeho pohyb. A pritom sa kinetická energia líši a je schopná zvýšiť alebo znížiť.

Ak častica alebo objekt prechádza z bodu A do bodu B, práca W_AB Potrebné sa rovná rozdielu medzi kinetickou energiou, ktorú mal objekt medzi bodom B a ten v bode Do:

W_AB = K_B - Klimatizovať_Do = ΔK = w_slepo

Symbol „δ“ znie „delta“ a symbolizuje rozdiel medzi konečnou veľkosťou a počiatočnou veľkosťou. Teraz sa pozrime na konkrétne prípady:

-Ak je práca vykonaná na objekte negatívna, znamená to, že sila sa postavila proti pohybu. Preto kinetická energia pokles.

-Na druhej strane, keď je práca pozitívna, znamená to, že sila uprednostňuje pohyb a kinetickú energiu zvýšenie.

-Môže sa stať, že sila nefunguje na objekte, čo neznamená, že je stále. V tomto prípade kinetická energia tela nemení sa.

Keď sa lopta vyhodí zvisle nahor, počas nahrávania gravitácia robí negatívnu prácu a lopta brzdí, ale na smerovaní smerom nadol gravitáciou uprednostňuje pokles zvýšením rýchlosti.

Môže vám slúžiť: rovnomerne zrýchlený priamy pohyb: Charakteristiky, vzorce

Nakoniec, tie objekty, ktoré majú rovnomerný priamy pohyb alebo jednotný kruhový pohyb, nezažívajú variácie v ich kinetickej energii, pretože rýchlosť je konštantná.

Vzťah medzi kinetickou energiou a okamihom

Lineárny moment alebo spád Je to vektor označený ako P. Nemalo by sa zamieňať s hmotnosťou objektu, iným vektorom, ktorý sa často označuje rovnakým spôsobom. Moment je definovaný ako:

P = m.vložka

Kde m je hmotnosť a V je veloc vektor tela. Rozsah momentu a kinetická energia udržiavajú určitý vzťah, pretože závisia od hmotnosti a rýchlosti. Môžete ľahko nájsť vzťah medzi týmito dvoma veľkosťami:

K = ½ mv² = (Mv)² / 2m = P² /2 m

Dobrá vec na nájdení vzťahu medzi momentom a kinetickou energiou alebo medzi momentom a inými fyzikálnymi veľkosťami je, že tento moment sa zachováva v mnohých situáciách, napríklad počas zrážok a iných zložitých situácií. A to uľahčuje nájdenie riešenia problémov tohto typu.

Ochrana kinetickej energie

Kinetická energia systému nie je vždy zachovaná, s výnimkou určitých prípadov ako v dokonale elastických kolíziách. Tie, ktoré sa odohrávajú medzi takmer nedeformovateľnými predmetmi, ako sú biliardové gule a subatomické častice, sú veľmi blízko k tomuto ideálu.

Počas dokonale elastickej zrážky a za predpokladu, že je systém izolovaný, môžu častice navzájom prenášať kinetickú energiu, ale s podmienkou, že súčet jednotlivých kinetických energií je konštantný.

Vo väčšine kolízií sa to však nestane, pretože určité množstvo systémovej kinetickej energie sa transformuje na kalorickú, deformáciu alebo zvukovú energiu.

Napriek.

Cvičenia

- Cvičenie 1

Zasiahla sa sklenená váza, ktorej cesto je 2.40 kg z výšky 1.30 m. Vypočítajte svoju kinetickú energiu tesne pred dosiahnutím zeme, bez toho, aby ste zohľadnili odpor vzduchu.

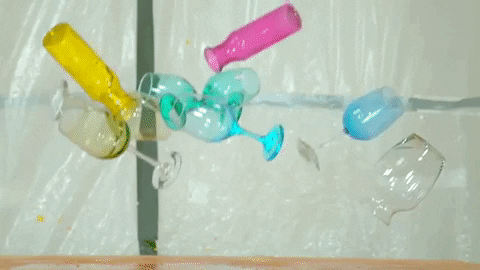
Riešenie

Ak chcete uplatniť kinetickú energetickú rovnicu, je potrebné poznať rýchlosť vložka S prichádza váza na zem. Je to voľný pád a celková výška je k dispozícii h, Preto pri používaní kinematických rovníc:

vložka_F² = v_ani² +2gh

V tejto rovnici, g Je to hodnota zrýchlenia gravitácie a v_ani Je to počiatočná rýchlosť, ktorá je v tomto prípade 0, pretože váza klesla, preto:

vložka_F² = 2gh

S touto rovnicou môžete vypočítať štvorec rýchlosti. Všimnite si, že rýchlosť nie je potrebná, odvtedy K = ½ mv². Môžete tiež vymeniť štvorcovú rýchlosť v rovnici za Klimatizovať:

K = ½ m (2gh) = mgh

A nakoniec sa vyhodnocuje s údajmi uvedenými vo vyhlásení:

Môže vám slúžiť: eliptické galaxie: formovanie, charakteristiky, typy, príklady

K = 2.40 kg x 9.8 m/s² x 1.30 m = 30.6 J

Je zaujímavé poznamenať, že v tomto prípade kinetická energia závisí od výšky, z ktorej váza klesá. A ako sa očakávalo, kinetická energia vázy sa zvyšovala od začiatku jej pádu. Je to preto, že gravitácia robila pozitívnu prácu na váze, ako je vysvetlené vyššie.

- Cvičenie 2

Kamión, ktorého hmotnosť je m = 1 250 kg má rýchlosť vložka₀ = 105 km/h (29.2 m/s). Vypočítajte prácu, ktorú by brzdy mali urobiť, aby ju úplne zastavili.

Riešenie

Ak chcete vyriešiť toto cvičenie, musíte využiť vyššie uvedenú energiu pracovnej vety-City Energy:

W = k_Konečný - Klimatizovať_{počiatočný} = ΔK

Počiatočná kinetická energia je ½ MV_ani² A konečná kinetická energia je 0, pretože vyhlásenie hovorí, že kamión sa úplne zastaví. V tomto prípade sa práca, ktorú vykonali brzdy, investuje do celého rozsahu, aby zastavil vozidlo. Berúc do úvahy:

W = -½ mv_ani²

Pred výmenou hodnôt musia byť vyjadrené v jednotkách medzinárodného systému, aby sa získali jouly pri výpočte práce:

vložka₀ = 105 km/h = 105 km/h x 1 000 m/km x 1 h/3600 s = 29.17 m/s

A tak sa hodnoty nahradia v rovnici pre prácu:

W = - ½ x 1250 kg x (29.17 m/s)² = -531.805,6 J = -5.3 x 10⁵ J.

Všimnite si, že práca je negatívna, čo dáva zmysel, pretože sila brzdy je proti pohybu, ktorý vozidlo nesie, takže jej kinetická energia klesá.

- Cvičenie 3

V pohybe sú dve autá. Prvý má dvakrát toľko hmotnosti druhej, ale iba polovica svojej kinetickej energie. Keď obe autá zvýšia svoju rýchlosť o 5.0 m/s, ich kinetické energie sú rovnaké. Aké boli pôvodné rapides oboch automobilov?

Riešenie

Na začiatku má auto 1 kinetickú energiu k₁ a masa m₁, zatiaľ čo Car 2 má kinetickú energiu k₂ a masa m₂. Je tiež známe, že:

m₁ = 2 m₂ = 2 m

Klimatizovať₁ = ½ k₂

S ohľadom na to je napísané: Klimatizovať₁ = ½ (2 m) v₁²  a Klimatizovať₂ = ½ mv₂²

To je známe Klimatizovať₁ = ½ k₂, čo znamená, že:

Klimatizovať₁ = ½ 2MV₁² = ½ (½ mV₂²)

Preto:

2V₁² = ½ V₂²

vložka₁² = ¼ V₂² → V₁  = V₂ /2

Potom hovorí, že ak sa rapides zvýšia na 5 m/s, kinetické energie sa vyrovná:

½ 2 m (v₁ + 5)² = ½ m (v₂+ 5)² → 2 (v₁ + 5)² = (v₂+ 5)²

Vzťah medzi oboma Rapides je nahradený:

2 (v₁ + 5)² = (2v₁ + 5)²

Na oboch stranách sa nanáša druhý koreň, na vyčistenie V₁:

√2 (v₁ + 5) = (2v₁ + 5)

(√2 - 2) vložka₁ = 5 - √2 × 5 → -0.586 V₁ = -2.071 → V₁ = 3.53 m/s

vložka₂ = 2 V₁ = 7.07 m/s.

Odkazy

1. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill.
2. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 2. Dynamika. Editoval Douglas Figueroa (USB).
3. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6. Ed Prentice Hall.
4. Rytier, r.  2017. Fyzika pre vedcov a inžinierstvo: Strategický prístup. Pearson. 
5. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 1-2.