Elipsa

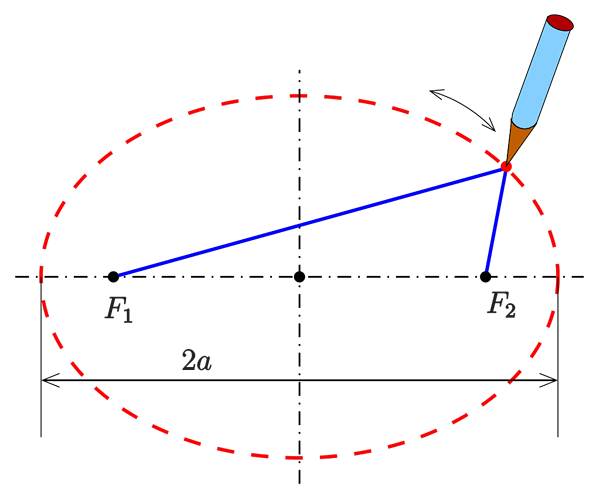
postava 1. Metóda záhradníka na kreslenie elipsy. Súčet vzdialenosti medzi bodom P elipsy (v červenej) a bodovými reflektormi (v čiernej) zostáva konštantný. Zdroj: Ag2gaeh, CC By-SA 4.0, cez Wikimedia Commons.

Čo je to elipsa?

Elipsa je sada súradnicových bodov (x, y), pre ktoré súčet vzdialenosti na dva pevné body nazývaný Foky, Je to konštantné. Reflektory sú naopak od seba oddelené vzdialenosť rovná 2c.

Elipsy sa nachádzajú v prírode. Napríklad je to v zemskom hnutí okolo Slnka, pretože ako to dokazuje nemecká astronóm.

Okrem toho sa eliptická forma nachádza v návrhu architektonických konštrukcií, je súčasťou lekárskeho ošetrenia, ktoré znižuje výpočty obličiek a slúži na formovanie rôznych objektov, ako sú tanky a iné nádoby.

Na hornom obrázku je elipsa znázornená s dvoma bodovými svetlami, ktoré sa nachádzajú rovnajúce od stredu obrázku a na najdlhšej osi. Podmienka, že bod P musí spĺňať, aby patril k elipse, je, že súčet vzdialeností každého zaostrenia je stanovený:

d₁ + d₂ = konštantný.

Preto, keď chce záhradník. Potom si vezmite lano dobrej veľkosti, priviažte svoje konce k stávkam a podoprite palicu na lane, ktoré na ňu posúva, aby označil eliptickú drážku na mäkkej zemi. To je metóda záhradníka Kresliť elipsy.

Elipse prvky

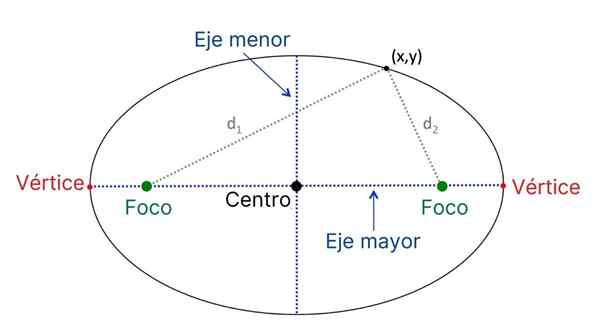Hlavné prvky elipsy

Toto sú hlavné prvky elipsy:

1. Foky, pevné body umiestnené na najdlhšej osi elipsy.
2. Vrcholy, Sú to dva body elipsy, cez ktoré prechádza čiara, ktorá sa pripojí k reflektorom.
3. Hlavná os, Je to lano, ktoré sa spája s vrcholmi a tiež obsahuje reflektory.
4. Stred, Stredný bod hlavnej osi, ktorý zodpovedá súradnicovému bodu (H, k). Každé zameranie je rovnomerné od stredu a na diaľku c to isté.
5. Menšia os, Je to lano, ktoré prechádza stredom a je kolmo na hlavnú os.
6. Vektorové rádiá, segmenty, ktoré sa spájajú s každým zameraním na p elipsy.
7. Ohnisková os, rovno, na ktorom sú bodové svetlá.
8. Ohnisková vzdialenosť, Je to vzdialenosť medzi bodovými svetlami označená ako 2c.
9. Sekundárna os, os kolmá na hlavnú os, ktorá je súčasne mediatrou segmentu, ktorá sa viaže na bodové svetlá.
10. Stredisko symetrie, bod, ktorý sa zhoduje so stredom elipsy, kde sú krížené osi symetrie.
11. Symetrické osi, Čiary obsahujúce najväčšie a menšie osi elipsy.

Môže vám slúžiť: zdaňovanie

Typy elipsy

Existujú dva typy elipsy:

• Tí, ktorí majú horizontálnu hlavnú os.
• Tí, ktorí majú najväčšiu vertikálnu os.

Potom sú opísané matematicky:

Ellipse s hlavnou horizontálnou osou

Nechajte bod C súradníc (H, k) stred elipsy, dĺžka hlavnej osi je 2a a dĺžka menšej osi rovnajúca sa 2b, s a> b.

Rovnica tejto elipsy je:

Elipsa s hlavnou vertikálnou osou

S rovnakými parametrami elipsy s horizontálnou osou je elipsa s hlavnou vertikálnou osou napísaná ako:

V obidvoch prípadoch vzdialenosť od zaostrenia do stredu c Súvisí so sedimentami majorom a menším prostredníctvom:

c² = a² - B²

Príklady elipsov

Vodorovná elipsa

Nasledujúci obrázok zobrazuje elipsu, ktorej hlavná os je vodorovná. Stred je v bode (0,0) a reflektory v (-3.0) a (3,0). Bod p (0, -4) zvýraznený patrí do elipsy.

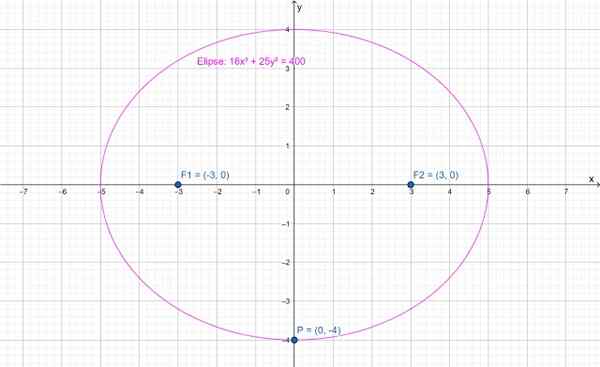Obrázok 2.- Ellipse, ktorej hlavná os je vodorovná. Zdroj: f. Zapata cez geogebra.

Rovnica tejto elipsy je:

16x² + 25 a² = 400

Nie je ťažké vyjadriť túto rovnicu v kanonickej podobe, stačí rozdeliť všetky výrazy medzi 400 a pohodlne zjednodušiť (pozri cvičenie vyriešené neskôr).

Vertikálna elipsa

Nasleduje vertikálna elipsa, ktorej hlavná os sa zhoduje s osou a. Zameriava sa na bod (0,0) a jeho rovnica je:

36x² + 9y² = 324

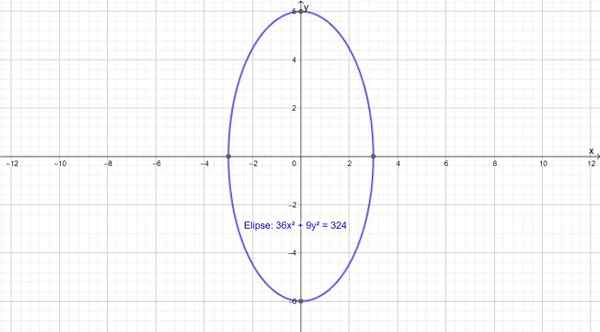Obrázok 3.- Elipsa s hlavnou vertikálnou osou. Zdroj: f. Zapata cez geogebra.

Reflexia

Pozostáva z nasledujúcich: Ak je v jednom z elipsových bodov umiestnený reflektor alebo zdroj zvuku, emitované vlny sa odrážajú smerom k druhému zaostreniu. Je to dobrý spôsob, ako presmerovať vlny, kde je potrebná vaša energia.

Môže vám slúžiť: endacegon

Preto v eliptických sálach, keď človek hovorí, že je v jednom z bodov, poslucháč nachádzajúci sa v druhom Focus jasne počúva jasne.

A v medicíne sa táto odrazová vlastnosť používa na ničenie obličkových kameňov umiestnením pacienta do jedného z bodov eliptickej vane plnej vody, zatiaľ čo generátor ultrazvukových vĺn je umiestnený do druhého zaostrenia. Vlny sa odrážajú vo výpočtoch a fragmentujú ich v menších častiach, ktoré sa potom vylučujú močom.

Rádio SKA

Tento rádioteleskop je najväčší v jeho type a očakáva sa, že začne pracovať v roku 2021. Jeho povrch je 1 km štvorcový, a preto sa nazýva ska (v angličtine sú skratkou pre Poľa štvorcových kilometrov).

Pri využívaní odrazovej vlastnosti elipsov táto štruktúra pozostáva z usporiadania 3000 antén s eliptickým tvarom širokým asi 15 m, distribuovaných medzi Austráliou a Južnou Afrikou. S týmto nástrojom, 50 -krát citlivejší ako tí, ktorí sa momentálne používajú, sa očakáva, že sa pozrie na vesmír, keď bol ešte oveľa mladší: asi miliardu rokov sotva.

Obrázok 4.- Umelecká interpretácia Ska Radio Ska. Zdroj: Wikimedia Commons.

Cvičenie

Nájdite kanonické rovnice elipsov znázornených na obrázkoch 2 a 3 a v každom prípade určte dĺžky zmyslov väčšie a menšie, ako aj ohniskové vzdialenosti.

Riešenie

Pre vodorovnú elipsu, ktorej rovnica je 16x² + 25 a² = 400, všetky výrazy medzi 400 sú rozdelení, čo je výsledkom:

Môže vám slúžiť: Cotangent odvodené: výpočet, demonštrácia, cvičenia

 Čo je zjednodušené:

Semi -axis „A“ opatrenia 5 a najmenšie opatrenia „B“, ktoré sú varované aj pozorným pozorovaním obrázka. Pokiaľ ide o ohniskovú vzdialenosť, musíte:

c² = a² - B²

c² = 25 - 16 = 9 ⇒ c = √9 = 3

Preto C = 3 je vzdialenosť medzi stredom a jedným z bodov. Obe ložiská sú vzdialenosť 2c = 6.

Pokiaľ ide o vertikálnu elipse 36x² + 9y² = 324 máte:

Zjednodušenie:

c² = 36 - 9 = 27

C = √27 ≅ 5.2

Preto je vzdialenosť medzi bodovými svetlami 10.4 jednotky.

Odkazy

1. Hoffman, J. Výber matematických problémov. Zväzok 3.
2. Stewart, J. 2006. Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.
3. Vesmír. Elipsa. Získané z: Universoformulas.com.
4. Wikipedia. Poľa štvorcových kilometrov. Obnovené z: je.Wikipedia.orgán.
5. Zill, D. 1984. Algebra a trigonometria. McGraw Hill.