Frakčné rovnice
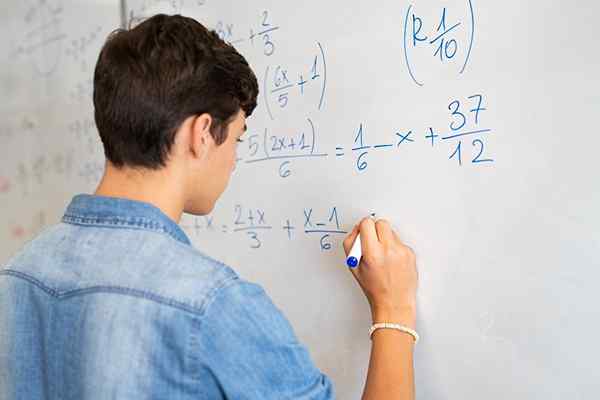
- 1436
- 276
- Denis Škriniar
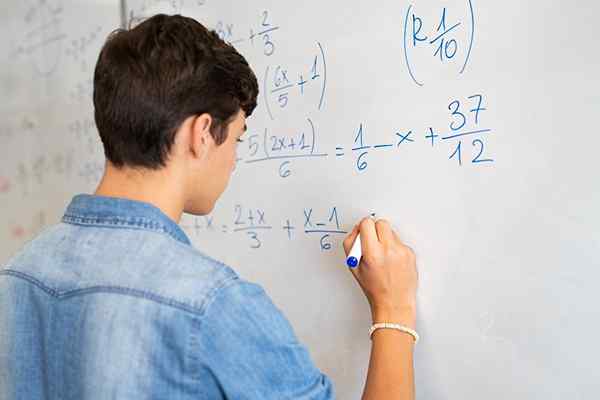 Frakčné rovnice zahŕňajú numerické a/alebo algebraické frakcie a neznáme môžu byť v čitateľovi a menovateľovi alebo oboje
Frakčné rovnice zahŕňajú numerické a/alebo algebraické frakcie a neznáme môžu byť v čitateľovi a menovateľovi alebo oboje Čo sú frakčné rovnice?
Ten frakčné rovnice sú tie, ktoré obsahujú frakcie v jednom alebo viacerých svojich podmienkach. Takéto frakcie môžu byť číselné alebo algebraické, kde sa neznáme nachádzajú v čitateľovi a/alebo v menovateľovi akéhokoľvek termínu.
Potom niekoľko príkladov frakčných rovníc s jediným neznámym:
Prvým príkladom je lineárna rovnica s frakčnými koeficientmi; V druhom príklade je neznámy v menovateľovi každého z podmienok a v poslednom je neznáme čitateľ aj v menovateľovi.
Na ich vyriešenie je potrebné vykonať niektoré algebraické transformácie, a tak získať ekvivalentnú rovnicu, v ktorej sa neznáma neobjaví v menovateľovi. Po vykonaní tohto postupu sa riešenie nachádza pomocou vhodných techník.
Riešenie pozostáva zo súboru hodnôt „x“, ktoré spĺňajú rovnosť. Môže to byť jedinečná hodnota alebo niekoľko, ale v každom prípade je veľmi dôležité mať na pamäti, že nie všetky riešenia v ekvivalentnej rovnici sú prijateľné k pôvodnej rovnici.
Ak ide o rovnicu, ktorej neznámy je v menovateľovi, hodnoty „x“, ktoré sa jej zrušujú. Je to preto, že rozdelenie medzi 0 nie je definované.
Ak má ekvivalentná rovnica jedinečné riešenie a ukáže sa, že menovateľ ktoréhokoľvek z podmienok pôvodnej rovnice je zrušený, potom nemá žiadne riešenie.
Ako vyriešiť frakčnú rovnicu
Operácie, ktoré sa vykonávajú s cieľom vyriešiť nefrakčné rovnice, sú platné za predpokladu, že sa zachováva rovnosť. Týmto spôsobom môžete vo frakčnej rovnici pridať alebo odpočítať rovnaké množstvo na obidve strany rovnosti, vynásobte všetky výrazy rovnakým sumou alebo rozdeliť každý termín rovnakým sumou (odlišné od 0).
Môže vám slúžiť: Bolzano vetaAle keďže frakčná rovnica je potrebná na transformáciu na iný ekvivalent bez menovateľov, dodržiavajú sa aj nasledujúce všeobecné indikácie:
- Nájdite minimálny spoločný násobok menovateľov (m.c.m).
- Vynásobte každý termín m.c.m., S cieľom eliminovať menovateľov.
- Vyriešiť získanú ekvivalentnú rovnicu.
- Overte, či riešenia zistili, že spĺňajú pôvodnú rovnosť.
Typy rovnocenných rovníc
Ekvivalentné rovnice získané po uvedenom postupe môžu byť:
- Lineárny alebo prvý stupeň
- Kvadratický
- Vyšší poriadok
Vyriešené príklady
Príklad 1
Vyriešiť nasledujúcu rovnicu:
Je potrebné poznamenať, že rovnica je prvý stupeň v „x“, pretože „x“ je vysoký na 1. Koeficienty rovnice sú frakcie a spôsob, ako ich eliminovať, pracovať s celkovými číslami, vynásobí všetky výrazy minimálnym násobkom menovateľov (m (.c.m.).
m.c.m. (2,3,6) = 6
Tak:
3x - 2x = 1
x = 1
Čitateľ môže skontrolovať platnosť tohto riešenia, nahradiť x = 1 v pôvodnej rovnici a overiť, či sa získa rovnosť.
Príklad 2
Určite hodnoty „x“, ktoré uspokojujú:
Na rozdiel od predchádzajúceho príkladu sa v tomto prípade neznáme nachádza v menovateľovi. Všimnite si, že menovatelia sú zrušené pre hodnoty x = 2 a x = −1, detail, ktorý je vhodné vziať do úvahy, pretože ak ekvivalentná rovnica pripúšťa tieto riešenia, musíme ich vyradiť, pretože nie sú prípustní v pôvodnej rovnici.
Teraz musíme transformovať rovnicu na inú bez menovateľov, prvým krokom je urobiť súčet výrazov vľavo od rovnosti:
Pretože menovatelia sú rovnakí, takže je splnená rovnosť, je potrebné, aby boli čitatelia tiež:
Môže vám slúžiť: konštanta proporcionality: čo je, výpočet, cvičenia4 (x+1) - 3 (x -2) = 8
Stačí vyriešiť túto rovnicu, ktorá sa ukáže ako prvá trieda:
4x + 4 - 3x + 6 = 8
x = 8 - 6 - 4 = - 2
x = - 2
Pretože táto hodnota sa líši od zakázaných hodnôt, pripúšťa sa ako riešenie pôvodnej rovnice.
Príklad 3
Nájdite riešenie:
V tejto rovnici hodnota x = 4 ruší menovateľov, preto je vylúčená zo súboru riešenia transformovanej rovnice, ak sa objaví.
Transformovaná rovnica sa dá ľahko nájsť, stačí vynásobiť všetky výrazy podľa faktora (x-4):
Zostať:
2x - 4 = 4
2x = 8
x = 4
Príklad 4
Vyriešiť rovnicu:
V tomto prípade majú menovatelia kvadratické pojmy, takže je vhodné ich najskôr zohľadniť:
- X2 + 8x + 7 = (x + 7) (x + 1)
- X2 - 49 = (x + 7) (x - 7)
- X2 - 6x - 7 = (x - 7) (x + 1)
Rovnica je taká:
Hodnoty x, ktoré rušia ktorýkoľvek z menovateľov, sú: x = −7, x = 7, x = −1. Preto, aj keď sú tieto hodnoty súčasťou množiny riešenia modifikovanej rovnice, nemôžu byť riešením pôvodnej rovnice.
Teraz prichádza proces transformácie rovnice. Prvým krokom je nájsť minimálny spoločný násobok menovateľov:
m.c.m. = (x + 7) (x - 7) (x + 1)
Vynásobením na oboch stranách rovnosti m.c.m. Zostane:
Výsledné:
(x - 7) (x- 2) = (x + 1) (2x - 5) - (x + 7) (x - 2)
Prostredníctvom distribučného vlastníctva sa vyvíjajú výrobky:
X2 - 9x +14 = 2x2 - 3x - 5 - (x2 + 5x - 14)
Zníženie podobných výrazov na pravej strane:
X2 - 9x + 14 = x2 - 8x + 9
Kvadratické výrazy sú zrušené splnením toho istého znamenia na rôznych stranách rovnosti:
Môže vám slúžiť: Rozdiel kociek: vzorce, rovnice, príklady, cvičenia- 9x + 14 = - 8x + 9
-x = -5 ⇒ x = 5
Tento výsledok je pripustený ako riešenie, pretože to nie je žiadna z zakázaných hodnôt.
Aplikačné cvičenie zlomkových rovníc
Menovateľ frakcie presahuje štyri jednotky pre čitateľa. Ak sa čitateľ odpočíta od čitateľa a tiež menovateľa, výsledná frakcia je 3/5. Určite pôvodný zlomok.
Riešenie
Nech x je hodnota čitateľa.
Pretože menovateľ frakcie presahuje štyri jednotky pre čitateľa, pôvodná frakcia je:
Teraz musíte odpočítať 5 jednotiek, čitateľovi aj menovateľovi:
Pretože frakcia vyplývajúca z vykonávania predchádzajúceho postupu sa rovná 3/5, vyrovnávajú sa:
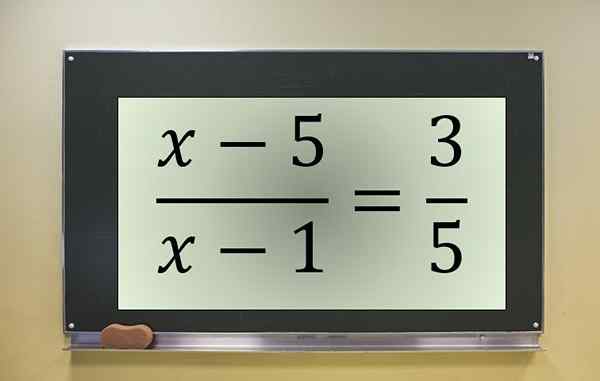 Príklad frakčnej rovnice. Zdroj: f. Zapata.
Príklad frakčnej rovnice. Zdroj: f. Zapata. Toto je frakčná rovnica s neznámym v čitateľovi a menovateľovi, ktorá je zrušená pri x = 1. Preto musí byť táto hodnota vylúčená, ak bola medzi roztokmi transformovanej rovnice.
Potom vynásobí obe strany minimálnym bežným násobkom, ktorý je 5 (x - 1):
Výsledkom nasledujúcej rovnocennej rovnice:
5 (x - 5) = 3 (x - 1)
Uplatňovanie distribučnej vlastnosti:
5x -25 = 3x - 3 ⇒ 2x = 22
x = 11
Pôvodná frakcia nahrádza x = 11 vo výraze:
Výsledkom frakcie 11/15. Toto je odpoveď na nastolený problém.
Odkazy
- Frakčné rovnice. Získané z: MatHepower.com
- Matematický portál. Frakčné rovnice. Riešenie problémov. Získané z: Silvioduarte.com.
- Stewart, J. (2007). Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.
- Sullivan, m. (1997). Predbežné vyfarbenie. 4. Vydanie. Pearson Vzdelanie.
- Zill, D. (2008). Predbežné náskoky s výpočtovými pokrokmi. 4. Vydanie. McGraw Hill.



(x+1))

=6\left%20(%20\frac16%20\right%20))
-3(x-2)(x-2)(x+1)=\frac8(x-2)(x+1))
\left%20(%20\fracxx-4%20\right%20)+(x-4)=(x-4)\left%20(%20\frac4x-4%20\right%20))

(x+1)=\frac2x-5(x+7)(x-7)-\fracx-2(x-7)(x+1))
(x-7)(x+1)\left%20[%20\fracx-2(x+7)(x+1)%20\right%20]=(x+7)(x-7)(x+1)\left%20[%20\frac2x-5(x+7)(x-7)-\fracx-2(x-7)(x+1)%20\right%20])



\left%20(%20\fracx-5x-1%20\right%20)=5(x-1)\frac35)