Vzorec prvého stupňa, ako ich vyriešiť, napríklad cvičenia

Ten Prvé alebo lineárne rovnice S neznámymi sú tie, ktoré možno vyjadriť ako súčet dvoch termínov nasledujúcim spôsobom:

AX + B = 0

Kde a b, s do ≠ 0, sú reálne čísla r alebo tiež komplexy c. Na jeho vyriešenie sa transponujú podmienky, čo znamená zmenu výrazov z jednej strany na druhú rovnosť.

postava 1. Lineárna rovnica je y = mx + c formu s y = 0. Zdroj: pxhere.

Na vyčistenie neznámeho termínu +B sa transponuje, ktorý musí ísť na pravú stranu rovnosti so zmeneným znakom.

AX = -B

Potom sa vymaže hodnota X týmto spôsobom:

x = - b/a

Ako príklad vyriešime nasledujúcu rovnicu:

6x - 5 = 4

Termín -5 premieňame na pravú stranu zmeneným znakom:

6x = 4 + 5

To je rovnocenné s pridaním 5 na oboch stranách pôvodnej rovnice:

6x - 5 + 5 = 4 + 5 → 6x = 9

A teraz vymažeme neznáme „X“:

x = 9/6 = 3/2

Čo je rovnocenné rozdeleniu oboch strán rovnosti o 6. Takže môžeme vyhodnotiť nasledujúce, aby sme získali riešenie:

-Rovnaké množstvo je možné pridať alebo odpočítať obe strany rovnosti v rovnici, bez toho, aby ste ju zmenili.

-Môžete tiež vynásobiť (alebo rozdeliť) rovnakou sumou do všetkých výrazov vľavo, ako aj vpravo od rovnice.

-A ak obaja členovia rovnice stúpajú na rovnakú moc, rovnosť sa nezmení.

[TOC]

Ako vyriešiť rovnice prvého stupňa

Riešenie rovnice prvého stupňa je známe aj ako koreň toho istého. Je to hodnota X, ktorá premieňa pôvodný výraz na rovnosť. Napríklad v:

5x = 8x - 15

Ak nahradíme x = 5 v tejto rovnici, získa sa:

5 hlúpar

25 = 40 - 15

25 = 25

Keďže lineárne rovnice prvého stupňa prichádzajú mnohými spôsobmi, ktoré niekedy nie sú zrejmé, existuje séria všeobecných pravidiel, ktoré tvoria niekoľko algebraických manipulácií, aby sa našla hodnota neznáma:

-Po prvé, ak existujú uvedené operácie, musia sa vykonať.

-Symboly zoskupenia, ako sú zátvorky, štvorcové zátvorky a kľúče, ak existujú, musia byť potlačené udržiavaním vhodných príznakov.

-Podmienky sú transponované tak, aby umiestnili všetky, ktoré obsahujú neznáme na jednej strane rovnosti, a tie, ktoré ju neobsahujú na druhú.

-Potom sú všetky podobné výrazy znížené, aby ste dosiahli formulár AX = -B.

-A posledným krokom je vyčistiť neznáme.

Grafická interpretácia

Rovnica prvého stupňa zvýšená na začiatku môže byť odvodená z rovnice riadku y = mx+c, ktorá robí y = 0. Hodnota x, ktorá výsledky zodpovedá priesečníkovi čiary s horizontálnou osou.

Na nasledujúcom obrázku máte tri riadky. Počnúc zelenou čiarou, ktorej rovnica je:

Môže vám slúžiť: faktorizácia

y = 2x - 6

Vytvorenie y = 0 v riadku riadku sa získa rovnica prvého stupňa:

2x - 6 = 0

Ktorého roztok je x = 6/2 = 3. Teraz, keď podrobne opisujeme graf, je ľahké si uvedomiť, že v skutočnosti sa čiara rezne na horizontálnu os na x = 3.

Modrá čiara pretína os x pri x = 5, čo je riešenie rovnice -x + 5 = 0. Nakoniec, riadok, ktorej rovnica je y = 0.5x + 2 strihajte na os x pri x = -4, čo je ľahko varované pred rovnicou prvého stupňa:

0.5 x + 2 = 0

x = 2/0.5 = 4

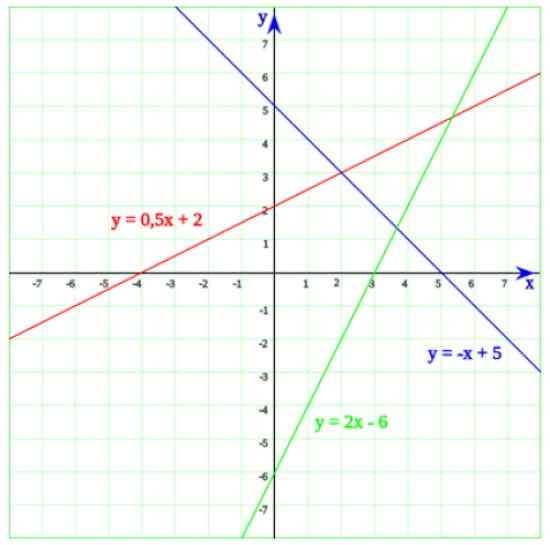Obrázok 2. Tri riadky, ktorých križovatky s horizontálnou osou zodpovedajú lineárnym rovniciam. Zdroj: Wikimedia Commons.

Príklady jednoduchých lineárnych rovníc   

Celé rovnice

Sú to tí, v ktorých pojmoch neexistujú žiadni menovatelia, napríklad:

21 - 6x = 27 - 8x

Jeho riešenie je:

-6x + 8x = 27 - 21

2x = 6

x = 3

Frakčné rovnice

Tieto rovnice obsahujú najmenej jeden iný menovateľ 1. Na ich vyriešenie je to vhodné.

Nasledujúca rovnica je frakčný typ:

Menovatelia sú 6, 8 a 12 a ich minimálny spoločný násobok označený ako m.c.M (6, 8,12) je najmenší z čísel obsahujúcich tieto menovateľov.

Pretože tieto čísla sú malé, nie je ťažké vidieť, že m.c.M (6, 8,12) = 24. Tento výsledok sa ľahko dosiahne vyjadrením čísel ako produktu prvých čísel alebo ich právomocí, pozrime sa:

6 = 3.2

8 = 2³

12 = 2²⋅3

Minimálny spoločný násobok sa určuje vynásobením bežných a nekomutníkových faktorov 6, 8 a 12 s jeho najväčším exponentom, potom:

MCM (6,8,12) = 2³ ⋅3 = 8 × 3 = 24

Pretože je k dispozícii minimálny časový násobok, musí sa vynásobiť každým z podmienok rovnice:

Týmto spôsobom sú menovatelia potlačení a existuje rovnica s výrobkami, ľahšie sa vyriešiteľná:

4 (x+5) -3 (2x+3) = 2 (1-5x)

Využívame distribučnú vlastnosť:

4x + 20 - 6x -9 = 2 - 10x

Všetky pojmy, ktoré obsahujú neznáme „x“, sú zoskupené na ľavú stranu rovnosti a zanechávajú nezávislé alebo numerické výrazy pravej strany:

4x - 6x + 10 x = 2 +9 - 20

8x = -9

x = - 9/8

Doslovné rovnice

Sú to lineárne rovnice s neznámymi, ktoré sú však sprevádzané doslovnými koeficientmi (listy). S týmito písmenami sa zaobchádza rovnako, ako by sa to stalo s číslami. Príkladom doslovnej prvej rovnice je:

-3AX + 2A = 5x - b

Táto rovnica sa vyrieši rovnakým spôsobom, ako keby boli nezávislé výrazy a koeficienty numerické:

-3AX - 5x = - b - 2a

Faktorovanie neznámeho „X“:

x (-3a - 5) = - b - 2a

x = ( - b - 2a) / (-3a - 5) → x = (2a + b) / (3a + 5)

Systémy rovníc prvého stupňa 

Systémy rovníc pozostávajú zo súboru rovníc s dvoma alebo viacerými neznámymi. Systémové riešenie pozostáva z hodnôt, ktoré spĺňajú rovnice súčasne a na ich jednoznačné určenie, musí existovať rovnica pre každé neznáme.

Môže vám slúžiť: Vektorová algebra

Všeobecná forma systému m Lineárne rovnice s n neznámy je:

do_jedenásťX₁ + do₁₂X₂ +.._1nX_n = b₁
do_{dvadsaťjeden}X₁ + do₂₂X₂ +.._2nX_n = b₂
..
do_M1X₁ + do_m2X₂ +.._mnX_n = b_m

Ak má systém riešenie, hovorí sa, že je určený kompatibilný, Ak existuje nekonečná skupina hodnôt, ktoré ju uspokojujú neurčitý kompatibilný, A nakoniec, ak nemá žiadne riešenie, potom je nezlučiteľný.

V rozlíšení lineárnych rovníc sa používa niekoľko metód: redukcia, výmena, vyrovnanie, grafické metódy, eliminácia Gauss-Jordan a použitie determinantov patria medzi najpoužívanejšie. Existujú však aj ďalšie algoritmy na dosiahnutie riešenia, vhodnejšie pre systémy s mnohými rovnicami a neznámymi.

Príklad systému lineárnych rovníc s dvoma neznámymi je:

8x - 5 = 7y - 9
6x = 3y + 6

Riešenie tohto systému je predložené neskôr v sekcii vyriešených cvičení.

Lineárne rovnice s absolútnou hodnotou

Absolútna hodnota skutočného čísla je vzdialenosť medzi jeho umiestnením na číselnom riadku a 0. Byť vzdialenosťou, jeho hodnota je vždy pozitívna.

Absolútna hodnota čísla je označená stĺpcami modulov: │x│. Absolútna hodnota kladného alebo záporného čísla je vždy pozitívna, napríklad:

│+8│ = 8

│-3│ = 3

V rovnici s absolútnou hodnotou je neznáme medzi stĺpcami modulov. Zvážte nasledujúcu jednoduchú rovnicu:

│x│ = 10

Existujú dve možnosti, prvé je, že X je kladné číslo, v takom prípade máme:

x = 10

A ďalšou možnosťou je, že X je v tomto prípade záporné číslo:

x = -10

Toto sú riešenia tejto rovnice. Teraz uvidíme iný príklad:

│x+6│ = 11

Suma v pruhoch môže byť pozitívna, potom:

x+6 = 11

x = 11 -6 = 5

Alebo môže byť negatívny. V tom prípade:

-(x+6) = 11

-x - 6 = 11 ⇒ -x = 11+6 = 17

A hodnota neznáma je:

x = -17

Táto rovnica absolútnej hodnoty má preto dve riešenia: x₁ = 5 a x₂ = -17. Môžeme overiť, či obe riešenia vedú k rovnosti v pôvodnej rovnici:

│5+6│ = 11

│11│ = 11

A

│-17+6│ = 11

│-11│ = 11

Jednoduché vyriešené cvičenia

- Cvičenie 1

Vyriešte nasledujúci systém lineárnych rovníc s dvoma neznámymi:

8x - 5 = 7y -9
6x = 3y + 6

Riešenie

Keďže tento systém je zdvihnutý, je vhodný na použitie metódy výmeny, pretože v druhej rovnici neznáme X Je takmer pripravený na povolenie:

x = (3y + 6)/6

Môže vám slúžiť: algebraic

A môžete okamžite nahradiť prvú rovnicu, ktorá sa potom stane prvou druhou rovnicou s neznámym „y“:

8 [(3y + 6)/6] - 5 = 7y - 9

Menovateľ môže byť potlačený, ak sa každý výraz vynásobí 6:

6 . 8lek [(3y + 6)/6] - 6.5 = 6 .7y- 6 . 9

8lek (3y + 6) - 30 = 42y - 54

Uplatňovanie distribučného majetku v prvom funkčnom období na právo na rovnosť:

24y + 48 -30 = 42y - 54 ⇒ 24y + 18 = 42y - 54

Rovnica sa dá zjednodušiť, pretože všetky koeficienty sú násobky 6:

4y + 3 = 7y - 9

-3y = -12

y = 4

Týmto výsledkom ideme k povoleniu X:

x = (3y +6)/6 → x = (12 +6)/6 = 3

- Cvičenie 2

Vyriešiť nasledujúcu rovnicu:

Riešenie

V tejto rovnici sa objavujú výrobky a podľa pokynov uvedených na začiatku sa musia vyvinúť ako prvé:

3x - 10x +14 = 5x + 36x + 12

Potom sa všetky výrazy obsahujúce neznámych prenášajú na ľavú stranu rovnosti a na pravej strane budú nezávislé výrazy:

3x - 10x - 5x - 36x = 12 - 14

-48x = -2

x = 1/24

- Cvičenie 3

Pridaním troch vnútorných uhlov trojuholníka sa získa 180 °. Najväčší presahuje dieťa v 35 °, čo zase presahuje rozdiel medzi najväčším a stredným. Aké sú uhly?

Riešenie

Zavoláme „X“ do hlavného uhla, „y“ k médiu a „z“ k dieťaťu. Keď sa vo vyhlásení uvádza, že ich súčet je 180 °, môžete napísať:

x + y + z = 180

Potom vieme, že najstarší presahuje dieťa v 35 °, môžeme napísať toto:

X = z + 35

Nakoniec dieťa presahuje 20 ° k rozdielu medzi najväčším a médiom:

Z = x - y + 20

Máme systém 3 rovníc a 3 neznámy:

x + y + z = 180

X = z + 35

Z = x - y + 20

Vymazaním prvej rovnice máte:

Z = 180 - x - y

Zodpovedanie tretieho:

180 - x - y = x - y + 20

Odovzdávanie neznámych na ľavú stranu ako vždy:

-x - y - x + y = 20 - 180

„Y“ je zrušený a zostáva:

-2x = - 160

x = 80 °

Druhou rovnicou je hodnota Z:

Z = x - 35 = 80 - 35 = 45 °

A hodnota a je z prvej alebo tretej:

y = 180 - x - z = 180 - 80 - 45 = 55 °

Odkazy

1. Plechovka. 1977. Elementárna algebra. Venezuelské kultúrne vydania.
2. Inštitút Monterey. Rovnice, nerovnosti a absolútna hodnota. Získané z: Montereyinstitute.orgán.
3. Online učiteľ. Klasifikácia lineárnych alebo prvotriednych rovníc. Získané z: profesor Inline.Cl.
4. Hoffman, J. Výber matematických problémov. Zväzok 2.
5. Jiménez, r. 2008. Algebra. Sála.
6. Zill, D. 1984. Algebra a trigonometria. McGraw Hill.