Všeobecná parabola rovnica (príklady a cvičenia)

Ten Podobenstvá všeobecná rovnica obsahuje kvadratické výrazy v X a v a, ako aj lineárne výrazy v oboch premenných plus nezávislý pojem. Prvá os symetrie je rovnobežná s vertikálnou osou a druhou je horizontálna os.

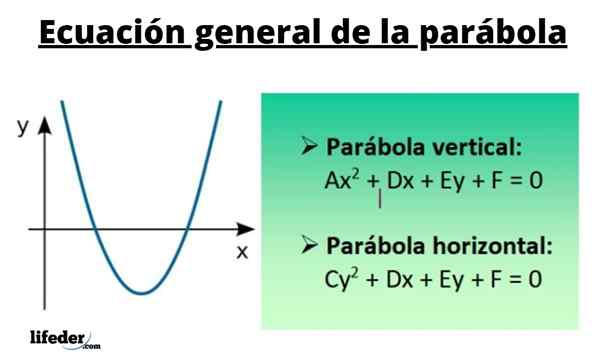
Všeobecne platí, že kvadratická rovnica, ktorá nemá prekročený termín Xy Je napísané ako:

Sekera² + Cy² +DX + EY + F = 0

Hodnoty A, C, D, E a F sú skutočné čísla. Ukladanie podmienok pri ∙ C = 0 a A+C ≠ 0, krivka, ktorá je výsledkom grafu bodov, ktoré spĺňajú túto rovnicu, je parabola.

Prípad 1

Pre vertikálne podobenstvo je jej všeobecná rovnica:

Sekera² + DX + EY + F = 0

Kde a a e sa líšia od 0. Inými slovami, keď sa objaví termín s x², Podobenstvo je zvislé.

Prípad 2

Pokiaľ ide o horizontálne podobenstvo, ktoré máte:

Cy² + DX + EY + F = 0

Tu sa C a D líšia aj od 0, preto kvadratický výraz zodpovedá a².

V každom prípade je všeobecná rovnica podobenstva kvadratická v jednej z premenných a v druhom lineárne.

Podobenstvo

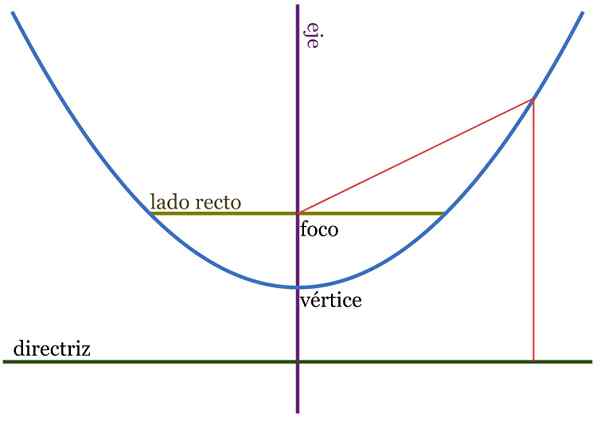Obrázok 2. Podobenstvo. Vzdialenosti qf a qh sú rovnaké. Zdroj: Wikimedia Commons.

Parabola, definovaná ako geometrické miesto, pozostáva zo súboru bodov jednej roviny, ktorá sa rovná inému bodu zvaného zameranie A tiež línie, známe ako usmernenie.

Z všeobecnej rovnice je možné študovať podobenstvo špecifikáciou jeho prvkov. Vrátane zamerania a usmernenia, tieto prvky, ktoré sú stručne opísané, sú:

-Osi, ktorá sa týka osi symetrie paraboly, môže byť vodorovná (rovnobežná s osou Abscissa) alebo vertikálne (rovnobežne s osou súradnicov).

Môže vám slúžiť: spoločný faktor pre zoskupovanie podmienok: príklady, cvičenia

-Orientácia, čo zase zodpovedá orientácii osi. Podobenstvo je zvislé, ak je jeho os symetrie zvislá a je vodorovná, keď je os tiež.

-Vrchol, Je to bod, v ktorom os pretínajú podobenstvo.

-Zameranie, bod umiestnený na osi, vo vnútri podobenstva a vo vzdialenosti p vrchol. Všetky body paraboly Ekridist na zameranie a smer usmernenia.

-Parameter, Je to vzdialenosť p Medzi zaostrením a vrcholom.

-Usmernenie, čo je kolmo na os y a tiež vzdialenosť p vrcholu podobenstva, ale nepretínne ho, pretože je na vonkajšej strane.

-Priama strana, Je to lano, ktoré prechádza zaostrením a pretína podobenstvo v dvoch bodoch, kolmo na jeho osi.

-Excentricita, že v prípade paraboly to vždy stojí 1.

-Grafická reprezentácia.

Informácie na určenie všetkých týchto prvkov sú obsiahnuté vo všeobecnej rovnici.

Kanonická forma

Na určenie prvkov paraboly, niekedy je vhodné odovzdať všeobecnú formu do kanonického tvaru toho istého pomocou metódy dokončenia štvorcov v kvadratickej premennej.

Táto kanonická forma je:

(X-H)² = 4p (y-k)

Kde bod (h, k) je vrchol v podobenstve. Kanonická forma pre všeobecnú rovnicu sa tiež môže stať, rozvíjať pozoruhodný produkt a usporiadať podmienky.

Príklady

Príklad 1

Všeobecne sú parabola rovnice:

a) 4x² + 5y - 3 = 0

b) 1 - 2y + 3x - a² = 0

V a) sú identifikované koeficienty: a = 4, c = 0, d = 0, e = 5, f = -3. Je to podobenstvo, ktorého os symetrie je zvislá.

Môže vám slúžiť: Syntetické rozdelenie

Pokiaľ ide o jeho časť, v b) všeobecná rovnica zostáva:

- a² + 3x - 2y + 1 = 0

A koeficienty sú: c = -1, d = 3, e = -2 a f = 1.

Príklad 2

Ďalšie podobenstvo je v kanonickej podobe:

(Y-1)² = 6 (x-3)

Na nájdenie svojej všeobecnej rovnice sa vyvíja pozoruhodný produkt a zátvorka sa vykonáva napravo:

a² -2y + 1 = 6x -18

Teraz sa odovzdávajú všetky podmienky vľavo a sú pohodlne zoskupené:

a² -2y + 1- 6x +18 = 0 → a² - 6x -2y + 19 = 0

Ako je kvadratický termín a² Je to vodorovné podobenstvo. Koeficienty sú:

C = 1; D = -6; E = -2, f = 19.

Vyriešené cvičenia

Cvičenie 1

Ďalšie podobenstvo sa uvádza všeobecne:

X² -10x -12y - 11 = 0

Žiada sa, aby to napísal v kanonickej podobe.

Riešenie

Prejdite na kanonickú formu sa dosahuje dokončením štvorcov, v tomto prípade v premennej x. Podmienky v X začínajú v zátvorkách:

(X² -10x) -12y - 11 = 0

Musíte transformovať to, čo je v zátvorkách, na dokonalý štvorcový trinomén, ktorý sa dosiahne pridaním 5², To sa prirodzene musí odpočítať, pretože inak sa výraz zmení. Zostáva to takto:

(X² -10x+5²) −12y - 11-5²= 0

Tri výrazy v zátvorkách tvoria perfektný štvorcový trinomén (X-5)². Dá sa skontrolovať vývojom tohto pozoruhodného produktu na potvrdenie. Teraz podobenstvo zostáva:

(X-5)² -12y -36 = 0

Nasleduje zohľadnenie výrazov mimo zátvorky:

(X-5)² -12 (y +3) = 0

To sa nakoniec zmení na:

(X-5)² = 12 (y +3)

Príklad 2

Nájdite prvky predchádzajúceho podobenstva a zostavte svoju grafiku.

Riešenie

Vrchol

Vrchol paraboly má súradnice V (5, -3)

Môže vám to slúžiť: hepagonálny hranol

Osi

Riadok X = 5.

Parameter

Pokiaľ ide o hodnotu parametra p ktorá sa objavuje v kanonickej forme: (X-H)² = 4p (y-k) porovnáva obe rovnice:

4p = 12

P = 12/4 = 3

Orientácia

Toto podobenstvo je vertikálne a otvára sa. Pretože vrchol je umiestnený pri x = 5, y = -3, potom je os symetrie vertikálna čiara x = 5.

Zameranie

Zamerajte sa na riadok x = 5, preto má tiež súradnicu x = 5.

Súradnica a Zameranie musia byť p-jednotky nad k, tj: p + k = 3 + (-3) = 0, potom je zaostrenie v bode (5,0).

Usmernenie

Je kolmá na os, preto je vo forme y = c, teraz, pretože vzdialenosť P od vrcholu je ďaleko od, ale mimo podobenstva, to znamená, že je vo vzdialenosti p pod K:

y = k -p = -3-3 = -6

Priama strana

Tento segment sa znižuje na podobenstvo, prechádza zaostrením a je rovnobežný s usmernením, preto je obsiahnutý v riadku y = 0.

Grafická reprezentácia

Dá sa ľahko získať z bezplatného online grafického softvéru, napríklad Geogebra. V vstupnom krabici je umiestnený nasledovne:

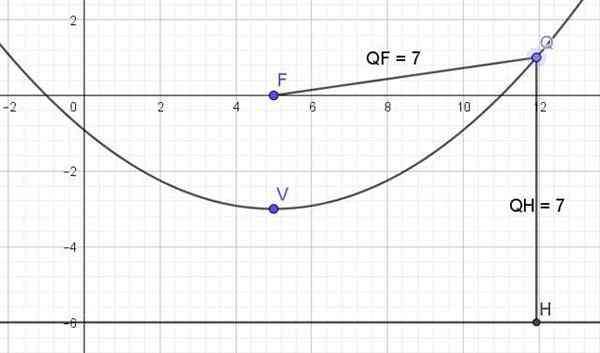Obrázok 3. Graf podobenstva x² -10x -12y - 11 = 0. Zdroj: f. Zapata.

Odkazy

1. Plechovka. 1977. Elementárna algebra. Venezuelské kultúrne vydania.
2. Hoffman, J. Výber matematických problémov. Zväzok 2.
3. Jiménez, r. 2008. Algebra. Sála.
4. Stewart, J. 2006. Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.
5. Zill, D. 1984. Algebra a trigonometria. McGraw Hill.