Domovská stránka
Matematika
Rovnomerné rozdelenie pokračuje v charakteristikách, príkladoch, aplikáciách

Matematika

Rovnomerné rozdelenie pokračuje v charakteristikách, príkladoch, aplikáciách

Náhodná premenná má a Kontinuálna jednotná distribúcia Ak je pravdepodobnosť prijatia hodnoty v konečnom intervale [a, b] rovnaká pre akýkoľvek podskupina rovnakej dĺžky.

Táto distribúcia je analogická s diskrétnou rovnomernou distribúciou, ktorá je priradená ku každému výsledku náhodného experimentu rovnaká pravdepodobnosť, ale v tomto prípade je premenná, ktorá sa má zohľadniť. Napríklad experiment, ktorý spočíva v výbere náhodného skutočného čísla, medzi hodnotami A a B, sleduje jednotné rozdelenie. Tu máte svoj graf:

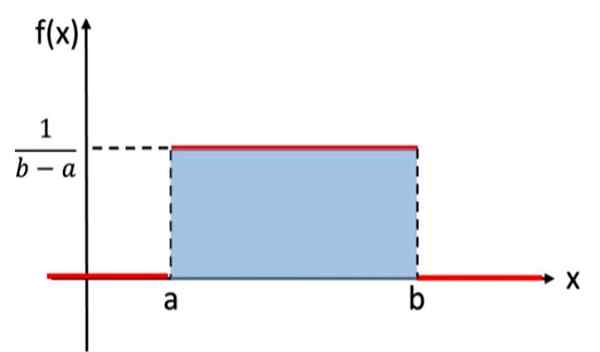
postava 1. Graf funkcie hustoty kontinuálneho normalizovaného rovnomerného rozdelenia

V matematickom notácii má kontinuálna rovnomerná distribúcia funkciu hustoty definovanú ako funkciu na kúsky alebo podľa sekcií, ktoré je možné písať ako:

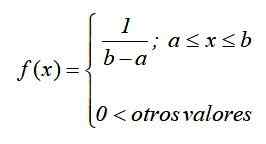
Graf tejto funkcie, známy ako Krivka alebo hustota, Je to obdĺžnik, takže kontinuálna rovnomerná distribúcia je známa aj ako obdĺžnikový distribúcia A je to najjednoduchšie nepretržité rozdelenie.

Oblasť v grafe distribúcie pravdepodobností sa rovná 1 a vždy má kladné hodnoty. Jednotné rozdelenie spĺňa tieto kritériá. Nie je potrebné priamo integrovať, aby sa overila, či je oblasť 1, pretože oblasť tieňovaného obdĺžnika na obrázku 1 sa dá vypočítať pomocou vzorca:

Oblasť = báza x výška = (b - a) x [1/(b - a)] = 1

Poznanie oblasti pod krivkou hustoty je veľmi dôležité, pretože existuje vzťah medzi oblasťou a pravdepodobnosťou výskytu udalosti, ktorá je pre túto distribúciu určená v nasledujúcej časti.

Kontinuálne rovnomerné distribučné charakteristiky

Kontinuálne rovnomerné rozdelenie sa vyznačuje jej:

Funkcia hustoty

Nech x je kontinuálna náhodná premenná, ktorá patrí do intervalu [a, b], potom:

Môže vám slúžiť: lineárne transformácie: Vlastnosti, aké sú použitie, typy, príklady

$f(X)=\frac1b-a$

Funkcia distribúcie

Prostredníctvom distribučnej funkcie sa vypočíta pravdepodobnosť, že náhodná premenná x berie hodnotu x z možných hodnôt intervalu [a, b]. Pre nepretržité rozdelenie sa všeobecne vypočíta týmto spôsobom:

$P(a\leq X\leq b)=\int_a^xf(x)dx$

V prípade kontinuálneho rovnomerného rozdelenia je uvedená pravdepodobnosť F (x) rovnocenná s obdĺžnikou, ktorej základňa je (X-A) a jej výška je (B-A):

$P(a\leq X\leq b)=\int_a^x\left (\frac1b-a \right )dx=\fracx-ab-a$

Matematicky, ak f (x) = pr (x = x) je podľa predchádzajúceho výsledku stanovená nasledujúca funkcia, podľa predchádzajúceho výsledku:

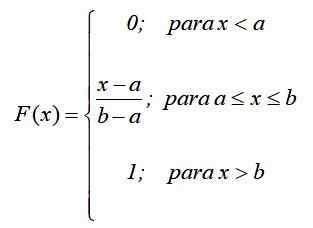
Týmto spôsobom, čo už bolo povedané: pravdepodobnosť závisí iba od hodnoty (X-A) a nie od jeho umiestnenia v intervale [a, b]. Graf distribučnej funkcie je:

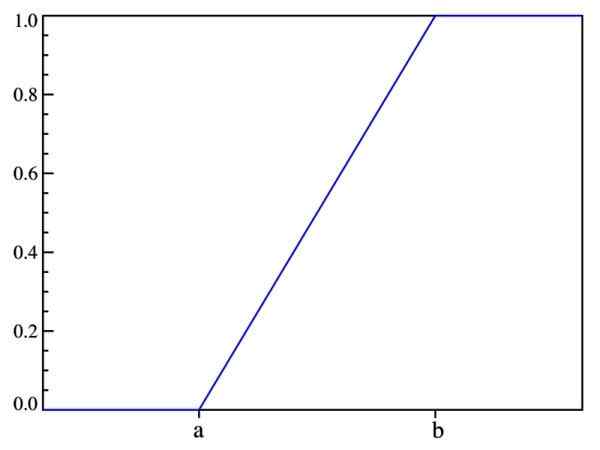Obrázok 2. Graf distribučnej funkcie f (x). Zdroj: Wikimedia Commons.

Očakávaná hodnota, rozptyl a štandardná odchýlka

Po vykonaní mnohých experimentov s nepretržitou náhodnou premennou sa jej priemerná hodnota nazýva očakávaná hodnota, Označuje sa ako e (x) a je vypočítaný podľa nasledujúceho integrálu:

$E(X)=\int_a^bxf(x)=\int_a^b\left (\frac1b-a \right )xdx=\left (\frac1b-a \right )\frac(b^2-a^2)2=\fraca+b2$ Pokiaľ ide o rozptyl, je definovaný:

V (x) = e (x²) - ex)²

Preto:

$V(X)=\left [\int_a^bx^2f(x)dx \right ]-\left (\fraca+b2 \right )^2=\left [\int_a^bx^2\left (\fracb-a2 \right ) dx\right ]-\left (\fraca+b2 \right )^2$

$V(X)=\frac(b-a)^212$ Nakoniec štandardná odchýlka je:

D (x) = √ V (x)

$D(X)=\sqrt\frac(b-a)^212$

Medián, móda, symetria a curtóza

Dá sa ľahko overiť, že medián, ktorý je ústrednou hodnotou jednotného rozdelenia, sa rovná priemeru, a keďže neexistuje žiadna hodnota, ktorá sa opakuje viac ako ostatné, pretože všetky sú rovnako pravdepodobné v intervale [a, b ], móda neexistuje.

Pokiaľ ide o symetriu, rovnomerná distribúcia je symetrická a curtóza, ktorá je stupňom, do akej sa hodnoty okolo stredu koncentrujú, je -6/5.

Môže vám slúžiť: Aké sú 7 prvkov obvodu?

Príklady

Rôzne situácie je možné modelovať prostredníctvom nepretržitého rozdelenia, a tak predpovedať ich správanie. Tu je niekoľko príkladov:

Príklad 1

Spoločnosť, ktorá poskytuje elektrickú službu, poskytuje rovnomerne distribuované úrovne napätia, medzi 123.0 v a 125.0 v. To znamená, že pri domácom záberu je možné získať akúkoľvek hodnotu napätia, ktorá patrí do tohto intervalu.

Potom, ako je uvedené vyššie, grafom funkcie hustoty je červený obdĺžnik:

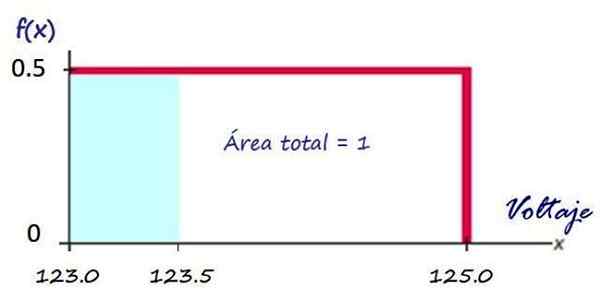Obrázok 3. Funkcia hustoty pre napätie dodávané elektrickou spoločnosťou. Zdroj: f. Zapata.

Výpočet pravdepodobnosti napätia v danom intervale je veľmi jednoduchý, napríklad, aká je pravdepodobnosť, že spoločnosť pošle napätie menšie ako 123.5 V?

Táto pravdepodobnosť je rovnocenná s plochou tieňovaného obdĺžnika v modrej farbe:

P (x<123.5) = (123.5 −123.0)x 0.5 = 0.25

A aká je pravdepodobnosť, že dodané napätie je väčšie ako 124.0 v?

Pretože celková plocha sa rovná 1, požadovaná pravdepodobnosť je:

P (x> 124.0 v) = 1 - (1 × 0.5) = 0.5

Dáva zmysel, od 124.0 je presne hodnota v strede intervalu.

Príklad 2

Určitá náhodná premenná X má v intervale rovnomernú distribúciu [0,100]. Určiť:

a) pravdepodobnosť, že hodnota x je menšia ako 22.

b) pravdepodobnosť, že x berie hodnoty medzi 20 a 35.

c) očakávaná hodnota, rozptyl a štandardná odchýlka tohto rozdelenia.

Odpovedať

Je určený podobne ako predchádzajúci príklad, ale najprv musíme určiť výšku obdĺžnika, nezabudnite, že celková plocha sa musí rovnať 1:

Oblasť = 100 × výška = 1

Preto obdĺžnik má výšku rovnajúcu sa 1/100 = 0.01

Môže vám slúžiť: decagon: pravidelné, nepravidelné, vlastnosti, príklady

P (x<22) = 22×0.01 = 0.22

Odpoveď B

Požadovaná pravdepodobnosť je ekvivalentná oblasti obdĺžnika, ktorej šírka je (35 - 20) a ktorej výška je 0.01:

P (22

Ak dávate prednosť tomu, aby ste prešli priamo do funkcie distribúcie vyššie, stačí nahradiť hodnoty v:

P (20

S f (x) danými:

F (x) = (x-a) / (b-a)

Hodnoty, ktoré sa majú zaviesť, sú:

A = 0

B = 100

F (35) = (35-0) / (100-0) = 0.35

F (20) = (20-0) / (100-0) = 0.dvadsať

P (20

Odpoveď c

Očakávaná hodnota je:

E (x) = (a+b)/2 = (100+0)/2 = 50

Rozptyl je:

V (x) = (b-a)²/12 = (100-0)²/12 = 833.33

A štandardná odchýlka je:

D (x) = √833.33 = 28.87

Žiadosti

Toto rozdelenie je užitočné, keď sa vykonávajú štatistické simulačné procesy alebo pri práci na udalostiach, ktorých frekvencia vzhľadu je pravidelná.

Náhodné čísla

Niektoré programovacie jazyky generujú náhodné čísla medzi 0 a 1, a ako je zrejmé z predchádzajúcich príkladov, distribúcia sledovaných pravdepodobností je jednotná. V tomto prípade je potrebné zvážiť interval [0,1].

Ľubovoľný odber distribúcie

Ak máte experiment, v ktorom majú udalosti pravidelnosť, ako je vysvetlené vyššie, môžete v zásade priradiť každému rovnakej pravdepodobnosti výskytu. V tomto prípade pravdepodobnostný model jednotnej distribúcie poskytuje informácie pre analýzu.

Zaokrúhlenie

Jednotné rozdelenie sa používa aj pri zaokrúhľovaní rozdielov medzi pozorovanými hodnotami a skutočnými hodnotami premennej za predpokladu rovnomerného rozdelenia chyby v danom intervale, podľa zaokrúhľovania, zvyčajne -0,5 až +0,5.

Odkazy

Berenson, m. 1985. Štatistiky pre správu a ekonomiku. Inter -American S.Do.
Canavos, g. 1988. Pravdepodobnosť a štatistika: Aplikácie a metódy. McGraw Hill.
Devore, J. 2012. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. 8. Vydanie. Cengage.
Levin, r. 1988. Štatistiky pre administrátorov. Druhý. Vydanie. Sála.
Triola, m. 2010. Štatistika. 11. Vydanie. Addison Wesley.
Walpole, r. 2007. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. Pearson.