Dynamika príkladov systému častíc, cvičení

Ten Dynamika systému častíc Skladá sa z uplatňovania Newtonových zákonov z pohybu na súbor častíc, ktoré môžu byť diskrétne (častice sa dajú spočítať) alebo byť súčasťou rozšíreného objektu, v tomto prípade je systém nepretržitý.

Aby sme vysvetlili pohyb systému častíc, je nepohodlné analyzovať každú z nich osobitne a zistiť, čo na ňu konajú sily. Namiesto toho je definovaný reprezentatívny bod súpravy, nazývaný Hromadné centrum.

Opis pohybu Mass Center ponúka veľmi úspešnú panorámu globálneho pohybu súboru, tiež umožňuje uplatňovať Newtonove zákony analogické, keď sa objekt považuje za častice bez rozmerov.

Tento posledný model, nazývaný časticový model, Je dobré opísať preklady a tiež vtedy, keď nie je potrebné brať do úvahy rozmery objektu. Ale bežné objekty sú veľkosťou a ak majú tiež rotačný pohyb, je potrebné vziať do úvahy body, na ktoré sa sily používajú.

[TOC]

Príklady

Zem a mesiac

Ilustrácia Zeme a Mesiaca

Sada diskrétnych častíc m₁, m₂, m₃... ktoré sa nakoniec pohybuje vzhľadom na pôvod súradníckeho systému, kvôli určitej výslednej sile, ktorá na ne pôsobí, je dobrým príkladom systému častíc.

Zem sa môže považovať za jednu častice a Mesiac druhý, potom obidve predstavujú systém 2 častíc pod pôsobením gravitácie slnka.

Rozšírené objekty

Osoba, zviera alebo akýkoľvek predmet životného prostredia, možno tiež považovať za systém častíc, iba to, že sú také malé, že človek nemôže spočítať jeden po druhom. Je to nepretržitý systém, ale berúc do úvahy určité úvahy, jeho zaobchádzanie je rovnaké ako v prípade diskrétneho systému.

Môže vám slúžiť: Čo je to školenie Entalpy? (S cvičeniami)

Tu sú podrobnosti.

Hmotnostné centrum systému častíc

Na začatie štúdia systému častíc musíte nájsť hmotnostné centrum (CM), čo je bod, v ktorom je celá hmotnosť systému koncentrovaná.

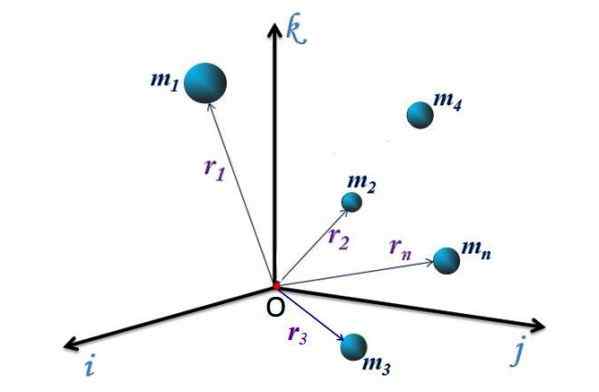
postava 1. Systém častíc v referenčnom systéme XYZ. Zdroj: f. Zapata.

Pre diskrétny systém na obrázku 1, s n častice, každý z nich má polohový vektor nasmerovaný z pôvodu alebo súradnice do bodu P (x, y, z), kde je častica. Tieto vektory sú označené ako r₁, r₂, r₃.. r_n.

Súradnice CM sa vypočítavajú podľa nasledujúcich rovníc:

Kde je každá z hmotností súpravy znázornená ako m₁, m₂, m₃... m_n. Všimnite si, že súčet ∑ m_Jo Je to ekvivalent celkovej hmotnosti m set. Ak je systém nepretržitý, zhrnutia sa nahradia integrálmi.

Každá z kolmých adries predstavuje jednotkové vektory Jo, J a klimatizovať, Preto vektor polohy CM označený r_Cm, Môže byť vyjadrený:

r_Cm = x_Cm Jo + a_Cm J + z_Cm klimatizovať

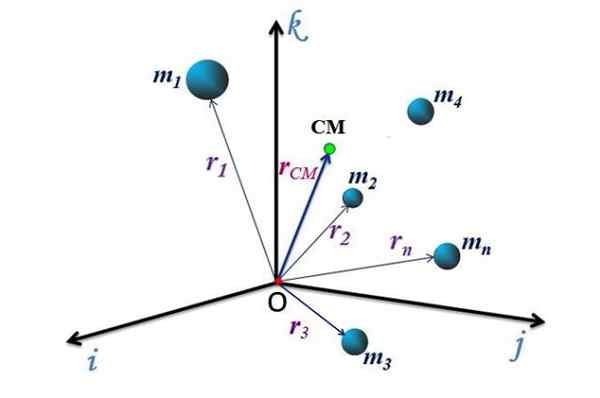Obrázok 2. Hromadné centrum systému častíc. Zdroj: f. Zapata.

Cm pohyb

Akonáhle je známa umiestnenie hmotnostného centra, použijú sa známe rovnice pohybu. Rýchlosť cm je prvá odvodená z polohy vzhľadom na čas:

V tomto prípade má systém celkové množstvo pohybu P ktorý sa počíta ako produkt celkovej hmotnosti systému a rýchlosti hmotnostného centra:

Môže vám slúžiť: Fyzická trajektória: Charakteristiky, typy, príklady a cvičenia

P = M ∙vložka_Cm

Celkové množstvo systému systému je možné vypočítať priamo:

P = m₁vložka₁ + m₂vložka₂ + m₃vložka₃ +.. . = ∑ m_Jo vložka_Jo

Zatiaľ čo zrýchlenie CM je odvodená rýchlosť:

Sila na CM

Sily pôsobiace na systém častíc môžu byť:

• Vnútorné sily v dôsledku interakcií medzi rovnakými časticami.
• Vonkajšie sily, spôsobené agentmi vonkajším systémom.

Keďže vnútorné sily sú prezentované pármi, rovnakého rozsahu a smeru, ale podľa tretieho zákona Newtonovho zákona je to opačné zmysly, splní sa to:

∑ F_int = 0

Preto vnútorné sily nemenia pohyb celku, ale sú veľmi dôležité na určenie vnútornej energie.

Ak je systém izolovaný a podľa Newtonovho zákona neexistujú žiadne vonkajšie sily. V opačnom prípade centrum hromadného prežíva zrýchlenie daného:

∑ F_rozšíriť = M ∙do_Cm

Kde m je celková hmotnosť systému. Predchádzajúcu rovnicu je možné napísať takto:

A to znamená, že vonkajšia sila je rovnocenná s dočasnou variáciou v množstve pohybu, čo je ďalší spôsob vyjadrenia Newtonovho druhého zákona a ten istý, ktorý používa slávny anglický fyzik vo svojej knihe Zásada.

Cvičenie

Hmotnostné stredisko 2 častíc je na osi x v určitom okamihu v polohe x = 2.0 m a pohyb s rýchlosťou 5.0 m/s rovnakým smerom a pozitívne. Ak je jedna z častíc na začiatku a druhá, hmotnosť 0.1 kg, je v pokoji pri x = 8.0 m, vypočítajte:

Môže vám slúžiť: diamagnetizmus: materiály, aplikácie, príklady

a) hmotnosť častíc, ktorá je na začiatku.

b) množstvo pohybu systému

c) Aká rýchlosť je častica, ktorá je na začiatku?

Roztok

Z rovnice pre polohu hmotnostného centra:

r_Cm = x_Cm Jo + a_Cm J + z_Cm K = 2.0 m Jo

Keďže CM má iba X súradnicu, používa sa prvú predtým danú trio rovnicu:

Súradnice sa teraz nahradia, ak je častica označená na začiatku, ako je napríklad číslo 1 a druhé, napríklad číslo 2, numerické údaje sú:

X₁ = 0 m, x₂ = 8.0 m, m₂ = 0.1 kg, x_Cm = 2.0 m

Zostať:

= 0.3 kg

Riešenie B

Množstvo pohybu systému sa vypočíta podľa:

P = M ∙vložka_Cm

Celková hmotnosť m sa rovná:

M = 0.3 kg + 0.1 kg = 0.4 kg

Preto:

P = 0.4 kg ∙ 5.0 m/s Jo = 2 kg.pani Jo

Riešenie c

Rovnice pre P Zo systému s dvoma účastníkmi sa vyčistí vložka₁, Pretože sú známe ostatné údaje, pretože vyhlásenie hovorí, že častice 2 je v pokoji, preto:

vložka₂ = 0 

A P Je to jednoducho ako:

P = m₁vložka₁

vložka₁ = P / m₁ = 2 kg.pani Jo / 0.3 kg = 6.67 m/s Jo

Odkazy

1. Vojvodská univerzita. Systémy častíc. Obnovené z: Webhome.Phy.Vojvoda.Edu.
2. Rex, a. 2011. Základy fyziky. Pearson.
3. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 1. Pearson.
4. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 1. 7. Edimatizovať. Učenie sa.
5. Tipler, P. (2006) Fyzika pre vedu a techniku. 5. vydanie. Zväzok 1. Redaktor sa vrátil.