Matematika

Rozdiel v vzorcoch, rovniciach, príkladoch, cvičeniach

Rozdiel v vzorcoch, rovniciach, príkladoch, cvičeniach

Ten Rozdiel kociek Je to binomická algebraická expresia formy3 - b3, kde pojmy A a B môžu byť reálne čísla alebo algebraické výrazy rôznych typov. Príklad rozdielu kociek je: 8 - x3, Pretože 8 je možné napísať ako 23.

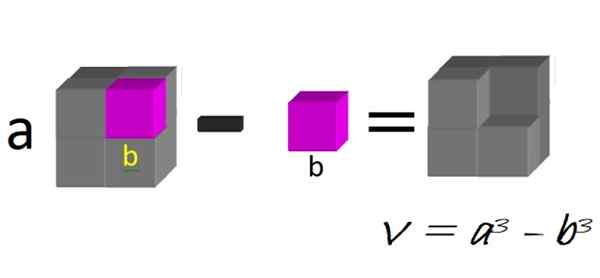
Geometricky dokážeme vymyslieť veľkú kocku, z boku A, na ktorú sa odpočíta malý Bube b strany B, ako je znázornené na obrázku 1:

postava 1. Rozdiel kociek. Zdroj: f. Zapata.

Objem výsledného obrázku je presne rozdiel v kocky:

V = a3 - b3

Na nájdenie alternatívnej expresie je pozorované, že toto číslo sa dá rozdeliť na tri hranoly, ako je to znázornené nižšie:

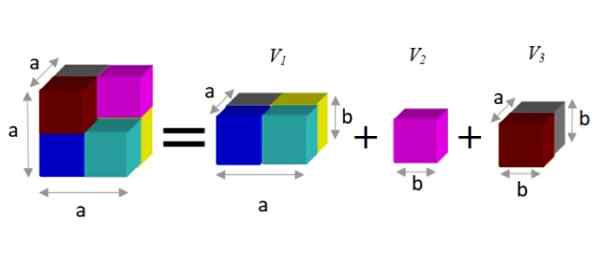Obrázok 2. Rozdiel v kocky (vľavo od rovnosti) sa rovná súčtu čiastočných objemov (vpravo). Zdroj: f. Zapata.

Prism má objem uvedený v produkte svojich troch rozmerov: šírka x vysoká x hĺbka. Týmto spôsobom je výsledný objem:

V = a3 - b3 = a2.B + B3 + do.b2

Faktor b Je to spoločné pre právo. Okrem toho na obrázku uvedenom vyššie je splnené najmä to, že:

b = (a/2) ⇒ a = b + b

Preto je možné povedať, že: b = a - b. Teda:

do3 - b3 = B (a2 + b2 +do.b) = (a-b) (a2 + do.B + B2)

Tento spôsob vyjadrenia rozdielu v kocky sa ukáže ako veľmi užitočný v mnohých aplikáciách a bol by získaný rovnakým spôsobom, hoci chýbajúca strana kocky v rohu bola odlišná od B = A/2.

Všimnite si, že druhá zátvorkaVyzerá to veľa na pozoruhodný produkt štvorca sumy, ale krížový výraz sa nevynásobí 2. Čitateľ môže vyvinúť pravú stranu, aby overil, či je efektívne získaná do3 - b3.

[TOC]

Môže vám slúžiť: Square Binomial

Príklady

Existuje niekoľko rozdielov kociek:

1 - m6

do6b3 - 8z12a6

(1/125).X6 - 27.a9

Poďme analizovať každú z nich. V prvom príklade je možné 1 napísať ako 1 = 13 a termín m6 Zostáva: (M2)3. Obe výrazy sú dokonalé kocky, preto ich rozdiel je::

1 -m6 = 13 - (m2)3

V druhom príklade sú podmienky prepísané:

do6b3 = (a2b)3

8z12a6 = 23 (z4)3 (a2)3 = (2z4a2)3

Rozdiel týchto kociek je: (a2b)3 - (2z4a2)3.

Nakoniec je frakcia (1/125) (1/53), X6 = (x2)3, 27 = 33 a a a9 = (a3)3. Nahradenie toho všetkého v pôvodnom výraze sa získa:

(1/125).X6  - 27 rokov9 = [(1/5) (x2)]3 - (3y3)3

Faktorizácia rozdielu kociek

Fakt Rozdiel v kocky zjednodušuje mnoho algebraických operácií. Na tento účel stačí použiť vzorec odpočítaný predtým:

Obrázok 3. Faktorizácia rozdielu v kocky a vyjadrovanie pozoruhodného kvocientu. Zdroj: f. Zapata.

Postup použitia tohto vzorca teraz pozostáva z troch krokov:

- Po prvé, kubický koreň každého z výrazov rozdielu sa získa.

- Potom sú postavené binomické a trinomiálne, ktoré sa objavujú na pravej strane vzorca.

- Nakoniec sa binomiálny a trinomén nahradí, aby sa získala konečná faktorizácia.

Použitie týchto krokov ilustrujeme s každým z príkladov rozdielu vyššie uvedených kociek, a tak získame jeho faktorizovaný ekvivalent.

Príklad 1

Faktický výraz 1 -m6   Podľa opísaných krokov. Začneme prepísaním výrazu ako 1 -m6 = 13 - (m2)3 Extrahovať príslušné kubické korene každého pojmu:

Potom sú postavené binomiálne a trinomiálne:

Môže vám slúžiť: Teória frontov: História, model, pre čo je pre to a príklady pre

A = 1

b = m2

Tak:

A - B = 1 - m2

 (2 +do.B + B2) = 12 + 1.m2 + (m2)2 = 1 + m2 + m4

 Nakoniec sa nahradí vo vzorci a3 - b3 = (a-b) (a2 +do.B + B2):

1 -m6 = (1 - m2) (1 + m2 + m4)

Príklad 2

Faktorizovať:

do6b3 -8z12a6 = (a2b)3 - (2z4a2)3

Pretože ide o dokonalé kocky, kubické korene sú okamžité: a2B a 2z4a2, Odtiaľ to nasleduje:

- Binomén: a2B - 2z4a2

- Trinomial: (a2b)2 + do2b. 2z4a2 + (2B +2z4a2)2

 A teraz je postavená požadovaná faktorizácia:

do6b3 -8z12a6 = (a2B - 2z4a2). ((k2b)2 + do2b. 2z4a2 + (2B + 2z4a2)2] =

= (a2B - 2z4a2). [4b2 + Druhý2b.z4a2 + (2B + 2z4a2)2]

V zásade je faktorizácia pripravená, ale často je potrebné zjednodušiť každý termín. Potom sa pozoruhodný produkt vyvinie zo súčtu - ktorý sa objaví na konci a potom pridá podobné výrazy. Pamätajte si, že štvorec sumy je:

(x + y)2 = x2 + 2xy + a2

Pozoruhodné právo na právo sa vyvíja týmto spôsobom:

(2B + 2z4a2)2 = a4b2 + 42b.z4a2 + 4z8a4

 Nahradenie vývoja získaného pri faktorizácii rozdielu v kocky:

do6b3 -8z12a6 = (a2B - 2z4a2). [4b2 + Druhý2b.z4a2 + do4b2 + 42b.z4a2 + 4z8a4] =

Nakoniec zoskupenie podobných pojmov a faktorovanie numerických koeficientov, ktoré sú všetky páry, sa získa:

(2B - 2z4a2). [24b2 + 62b.z4a2 + 4z8a4] = 2 (a2B - 2z4a2). [4b2 + Tretí2b.z4a2 + 2z8a4]

Príklad 3

Faktor (1/125).X6  - 27 rokov9 Je to oveľa jednoduchšie ako v predchádzajúcom prípade. Najprv sú identifikované ekvivalenty A a B:

A = (1/5) x2

B = 3y3

Potom sú nahradené priamo na vzorci:

(1/125).X6  - 27 rokov9 = [(1/5) x2 - 3y3]. [(1/25) x4 + (3/5) x2a3 + 9y6]

Cvičenie

Rozdiel v kocky, ako sme už povedali, má rôzne aplikácie v algebre. Pozrime sa na niektoré:

Môže vám slúžiť: 5 charakteristík karteziánskej roviny

Cvičenie 1

Vyriešiť nasledujúce rovnice:

a) x5 - 125 x2 = 0

b) 64 - 729 x3 = 0

Roztok

Najprv je rovnica faktorom týmto spôsobom:

X2 (X3 - 125) = 0

Keďže 125 je perfektná kocka, zátvorka je napísaná ako rozdiel v kocky:

X2 . (X3 - 53) = 0

Prvým riešením je x = 0, ale nájdeme viac, ak urobíme x3 - 53 = 0, potom:

X3 = 53 → x = 5

Riešenie B

Ľavá strana rovnice je prepísaná ako 64 - 729 x3 = 43 - (9x)3. Preto:

43 - (9x)3 = 0

Pretože exponent je rovnaký:

9x = 4 → x = 9/4

Cvičenie 2

Faktorizovať výraz:

(x + y)3 - (X - y)3

Riešenie

Tento výraz je rozdiel v kocky, ak vo vzorci faktorizácie si všimneme, že:

A = x+ a

b = x- y

Potom je binomiál postavený ako prvý:

a - b = x+ y - (x- y) = 2y

A teraz trinomiál:

do2 + do.B + B2 = (x+ y)2 + (x + y) (x-y) + (x-y)2

Vyvíjajú sa pozoruhodné výrobky:

(x+ y)2 = x2 + 2xy +a2

(x+y) (x-y) = x2- a2

(x- y)2 = x2 - 2xy +a2

Potom musíte nahradiť a znížiť podobné podmienky:

do2 + do.B + B2 = x2 + 2xy +a2+ X2- a2+ X2 - 2xy +a2 = 3x2 + a2

Výsledkom faktorizácie v:

(x + y)3 - (X - y)3 = 2y. (3x2 + a2)

Odkazy

  1. Baldor, a. 1974. Algebra. Venezuelské kultúrne redaktory.Do.
  2. Nadácia CK-12. Súčet a rozdiel kociek. Získané z: CK12.orgán.
  3. Khanská akadémia. Kocky rozdielovej faktorizácie. Obnovené z: je.Khanacademy.orgán.
  4. Matematika je zábavná pokročilý. Rozdiel dvoch kociek. Získané z: Mathsisfun.com
  5. Žobrák. Faktorizácia rozdielu kociek. Zdroj: DCB.Fi-c.Žobrák.mx.