Následné deriváty

Čo sú následné deriváty?

Ten následné deriváty Sú to odvodené z funkcie po druhom deriváte. Proces výpočtu nasledujúcich derivátov je nasledujúci: existuje funkcia F, ktorú môžeme odvodiť a získať odvodenú funkciu F '. K tomuto derivátu f ho môžeme znova odvodiť, získať (f ')'.

Táto nová funkcia sa nazýva druhý derivát; Všetky deriváty vypočítané z druhého sú následné; Tieto, tiež nazývané vyššieho poriadku, majú veľké aplikácie, ako napríklad poskytovanie informácií o zdvihu grafu funkcie, test druhého derivátu pre relatívne konce a stanovenie nekonečných sérií.

Definícia

Pomocou notácie Leibniz máme, že derivát funkcie „y“ vzhľadom na „x“ je DY/DX. Aby sme vyjadrili druhý derivát „y“ pomocou zápisu Leibnizu, píšeme takto:

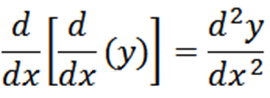
Všeobecne môžeme vyjadriť nasledujúce deriváty tak, že s notáciou Leibniza, kde n predstavuje poradie derivátu.

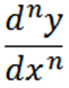
Ďalšie použité zápisy sú nasledujúce:

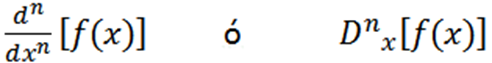
Niektoré príklady, kde vidíme rôzne zápisy, sú:

Príklad 1

Získajte všetky deriváty funkcie F definované:

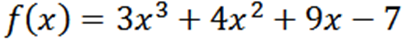
Pomocou obvyklých odporúčaní máme, že F je:

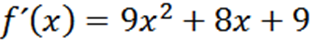
Opakovanie procesu, ktorý môžeme získať druhý derivát, tretí derivát atď.

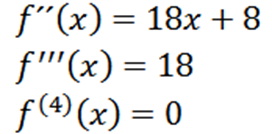
Všimnite si, že štvrtý derivát je nula a derivát nuly je nula, takže musíme:

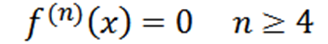
Príklad 2

Vypočítajte štvrtý odvodený z nasledujúcej funkcie:

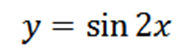
Odvodenie danej funkcie, ktorú máme v dôsledku toho:

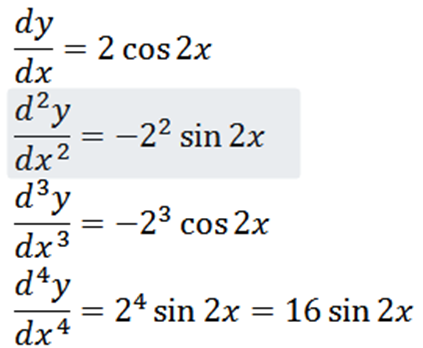
Rýchlosť

Jednou z motivácií, ktoré viedli k objavu derivátu, bolo hľadanie definície okamžitej rýchlosti. Formálna definícia je nasledovná:

Môže vám slúžiť: Primo čísla: Charakteristiky, príklady, cvičenia

Nech y = f (t) funkcia, ktorej graf v okamihu popisuje trajektóriu častice tón, Potom je jeho rýchlosť v okamihu T daná:

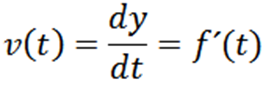
Po získaní rýchlosti častice môžeme vypočítať okamžité zrýchlenie, ktoré je definované takto:

Okamžité zrýchlenie častice, ktorej trajektória je daná y = f (t) je:

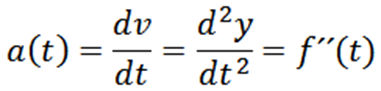
Príklad 1

Častica sa pohybuje po čiare podľa funkcie polohy:

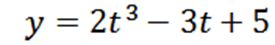
Kde sa „y“ meria v metroch a „t“ v sekundách.

• V akom okamihu je vaša rýchlosť 0?
• V akom okamihu je jeho zrýchlenie 0?

Odvodením funkcie „Y“ máme, že jej rýchlosť a zrýchlenie sa uvádza podľa:

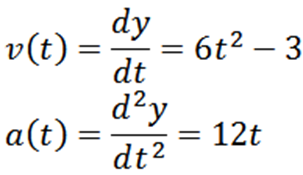
Aby sme odpovedali na prvú otázku, stačí určiť, kedy je funkcia V nula; toto je:

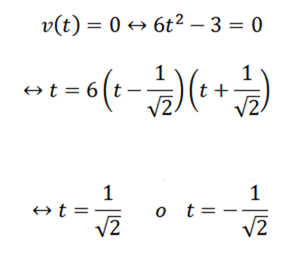
Pokračujeme v ďalšej otázke Analogous:

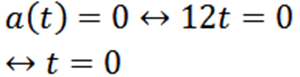
Príklad 2

Častica sa pohybuje po čiare podľa nasledujúcej rovnice pohybu:

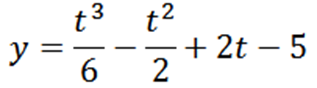
Určte „t, y“ a „v“, keď a = 0.

S vedomím, že rýchlosť a zrýchlenie je dané

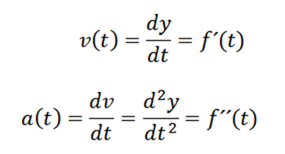
Pokračujeme v odvodení a získaní:

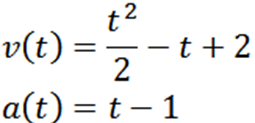
Robiť a = 0, máme:

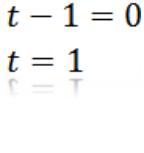
Kde dokážeme vyvodiť, že hodnota T, takže a je rovná nule, je t = 1.

Potom, vyhodnotenie v t = 1 funkcia polohy a funkcie, musíme:

Žiadosti

Derivácia mplícita

Postupné deriváty sa dajú získať aj implicitnou odvodením.

Príklad

Vzhľadom na nasledujúcu elipsu nájdete „y“:

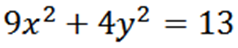
Implicitne odvodenie s ohľadom na X, máme:

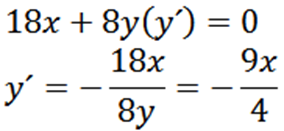
Potom nám dáva implicitne opätovné získanie s ohľadom na X:

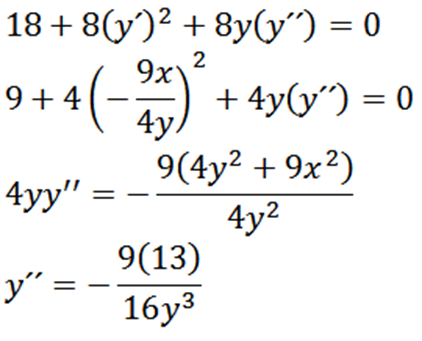
Nakoniec máme:

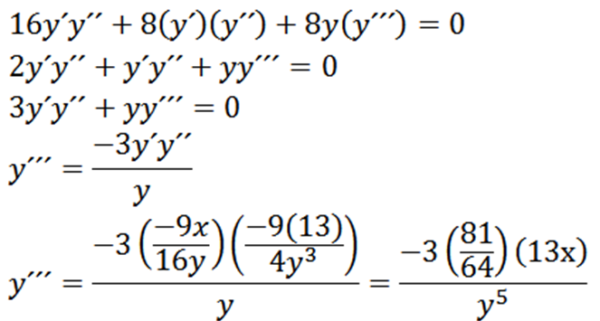
Relatívne extrémy

Ďalším použitím, ktoré môžeme dať derivátom druhého -rdéra, je výpočet relatívnych koncov funkcie.

Môže vám slúžiť: Koľko osí symetrie má kruh?

Kritériá prvého derivátu miestnych extrémov nám hovorí, že ak máme kontinuálnu funkciu F v intervale (a, b) a existuje C, ktorý patrí do uvedeného intervalu tak, že je zrušený v C (to znamená, že c je kritický bod), môže sa vyskytnúť jeden z týchto troch prípadov:

• Ak f '(x)> 0 pre akýkoľvek x patriaci k (a, c) a f' (x)<0 para x perteneciente a (c,b), entonces f(c) es un máximo local.
• Ak f '(x) 0 pre x patriace (c, b), potom f (c) je miestne minimum.
• Ak má f '(x) rovnaké znamenie (a, c) a v (c, b), znamená to, že f (c) nie je miestny koniec.

Použitím kritérií druhého derivátu môžeme vedieť, či je kritický počet funkcie maximálne alebo miestne minimum, bez toho, aby ste museli robiť to, čo je príznakom funkcie vo vyššie uvedených intervaloch.

Kritérium druhého driftu nám hovorí, že ak f '(c) = 0 a že f "(x) je kontinuálne v (a, b), stane sa, ak f" (c)> 0, potom f (c) je Miestne minimum a ak f "(c) < 0 entonces f(c) es un máximo local.

Ak f "(c) = 0, nemôžeme nič uzavrieť.

Príklad

Vzhľadom na funkciu f (x) = x⁴ + (4/3) x³ - 4x², Nájdite maximálny a minimálny príbuzný F Aplikácia kritérií druhého derivátu.

Najprv vypočítame f '(x) a f "(x) a máme:

f '(x) = 4x³ + 4x² - 8x

f "(x) = 12x² + 8x - 8

Teraz, f '(x) = 0 áno, a iba v prípade 4x (x + 2) (x - 1) = 0, a to sa vyskytuje, keď x = 0, x = 1 alebo x = - 2.

Aby sa určilo, či získané kritické čísla sú relatívnymi extrémami, ktoré sa len vyhodnotia v f “, a tak pozorujte jeho znamenie.

Môže vám slúžiť: Heptagon

f "(0) = - 8, takže f (0) je lokálne maximum.

f "(1) = 12, takže f (1) je miestne minimum.

f "(- 2) = 24, takže f (- 2) je miestne minimum.

Taylor Series

Byť funkciou definovaná takto:

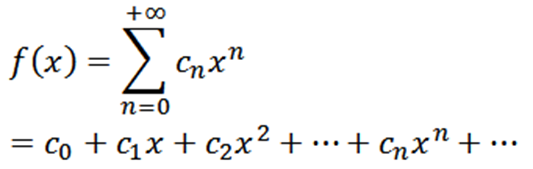
Táto funkcia má polomer konvergencie r> 0 a odvodila sa zo všetkých objednávok v (-r, r). Postupné deriváty F nám dajú:

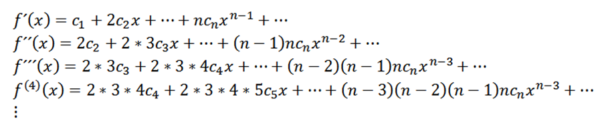
Užívanie x = 0, môžeme získať hodnoty C_n V závislosti od svojich derivátov nasledovne:

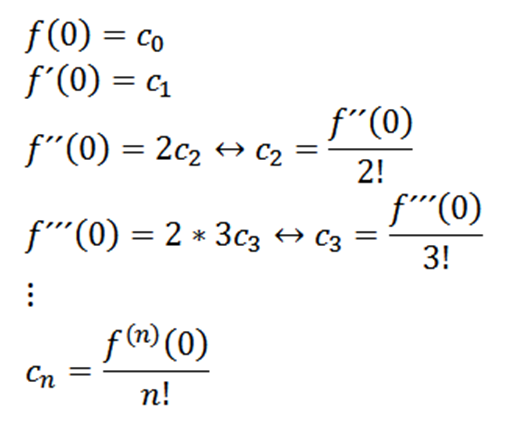
Ak vezmeme n = 0 ako funkciu f (tj, f^0 = f), potom môžeme túto funkciu prepísať nasledovne:

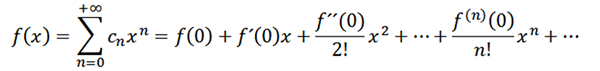
Teraz zvážme funkciu ako sériu síl pri x = a:

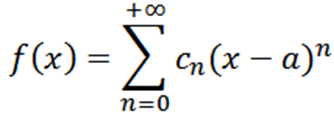
Ak vykonáme analýzu analogickú s predchádzajúcou, museli by sme napísať funkciu f ako:

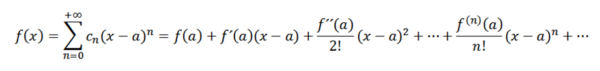
Tieto série sú známe ako Taylor F v sérii. Keď a = 0 máme konkrétny prípad nazývaný Maclaurin Series. Tento typ série má veľký matematický význam, najmä pri numerickej analýze, pretože vďaka týmto môžeme definovať funkcie v počítačoch ako e^X , Sin (x) a cos (x).

Príklad

Získajte sériu Maclaurin pre e^X.

Všimnite si, že ak f (x) = e^X, Potom f^(N)(x) = e^X a f^(N)(0) = 1, takže vaša séria Maclaurin je: