Vlastnosti čiastočných derivátov, výpočet, cvičenia

Ten čiastočné deriváty funkcie s niekoľkými nezávislými premennými sú tie, ktoré sa dosahujú pomocou bežného derivátu v jednej z premenných, zatiaľ čo ostatné sa udržiavajú alebo považujú za konštanty.

Čiastočné deriváty v jednej z premenných určuje, ako sa funkcia mení v každom bode, na jednotku zmeny príslušnej premennej. 

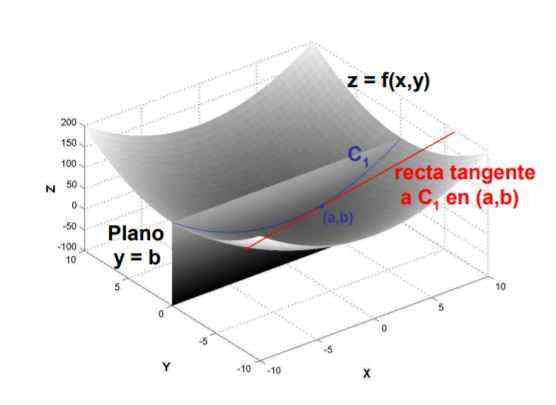postava 1. Sklon dotyčnice k krivke tvorenej priesečníkom roviny y = b s povrchom f (x, y) v bode (a, b) je čiastočne derivát f vzhľadom na x, vyhodnotený v tomto bode. Zdroj: UPM.je

Vďaka svojej definícii sa čiastočný derivát počíta matematický limit kvocientu medzi variáciou funkcie a variáciou premennej s ohľadom na to, čo sa odvodzuje, keď zmena posledne menovaná.

Predpokladajme prípad funkcie F Závisí to od premenných X a a, to znamená pre každý pár (X, y) A je pridelená z: 

f: (x, y) → z .

Čiastočné deriváty funkcie z = f (x, y), mať rešpekt z X je definovaný ako:

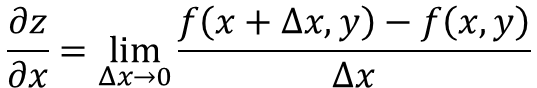
Teraz existuje niekoľko spôsobov, ako napríklad označovať čiastočné deriváty funkcie:

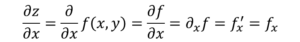
Rozdiel s bežným derivátom, pokiaľ ide o notáciu, je v tom, že d derivácie sa zmení na symbol ∂, Známy ako „Jacobi D“.

[TOC]

Vlastnosti čiastočných derivátov

Čiastočným derivátom funkcie niekoľkých premenných, vzhľadom na jednu z nich, je obyčajný derivát v uvedenej premennej a zvyšok považuje za pevné alebo konštantné. Na nájdenie čiastočného derivátu je možné použiť pravidlá odvodenia bežných derivátov.

Pod hlavnými vlastnosťami:

Môže vám slúžiť: spoločný faktor pre zoskupovanie podmienok: príklady, cvičenia

Kontinuita

Ak funkcia f (x, y) má čiastočné deriváty v X a a bod (Xo, ja) Potom je možné povedať, že funkcia je v tomto bode nepretržitá.

Pravidlo

Funkcia f (x, y) S nepretržitými čiastočnými derivátmi v X a a, čo zase závisí od parametra tón cez x = x (t) a y = y (t), Má obyčajný derivát vzhľadom na premennú tón, čo sa vypočíta podľa pravidla reťazca:

d_tón Z = ∂_Xz d_tónx + ∂_az d_tóna

Zatvorenie alebo uzamknutie vlastnosti

Čiastočný derivát vzhľadom na jednu z premenných funkcie F dvoch alebo viacerých premenných (X, y, ...), Je to ďalšia funkcia g Napríklad v tých istých premenných: 

G (x, y, ...) = ∂_a f (x, y, ...)

To znamená, že čiastočná derivácia je operácia, ktorá prechádza z Rⁿ rⁿ. V tomto zmysle sa hovorí, že je to zatvorená prevádzka.

Postupné čiastočné deriváty

Postupné čiastočné deriváty funkcie niekoľkých premenných je možné definovať, čo vedie k novým funkciám v rovnakých nezávislých premenných.

Byť funkciou f (x, y). Je možné definovať nasledujúce po sebe nasledujúce deriváty:

F_Xx = ∂_XF ;  F_Rizorný = ∂_RizornýF ; F_Xy = ∂_XyF a F_Yx = ∂_YxF

Posledné dva sú známe ako Zmiešané deriváty Pretože zahŕňajú dve rôzne nezávislé premenné.

Schwarzova veta

Byť funkciou f (x, y), definované takým spôsobom, že jeho čiastočné deriváty sú kontinuálne funkcie v otvorenej podskupine R².

Takže pre každé páry (X, y) Že patria k uvedenej podskupine, zmiešané deriváty sú rovnaké:

∂_XyF = ∂_YxF

Predchádzajúce vyhlásenie je známe ako Schwarzova veta.

Ako sa počítajú čiastočné deriváty?

Čiastočné deriváty sa počítajú podobne ako deriváty bežných funkcií v jednej nezávislej premennej. Keď sa s čiastočným derivátom funkcie niekoľkých premenných, pokiaľ ide o jednu z nich, ostatné premenné sa považujú za konštanty.

Môže vám slúžiť: polovica z 15

Nižšie je uvedené niekoľko príkladov:

Príklad 1

Byť funkciou:

f (x, y) = -3x² + 2 (a - 3)²

Žiada sa o výpočet prvého čiastočného derivátu vzhľadom na X a prvý čiastočný derivát s ohľadom a.

Postup

Na výpočet čiastočného F mať rešpekt z X, Je zabraný a ako konštanta:

∂_XF = ∂_X(-3x² + 2 (a - 3)² ) = ∂_X(-3x² )+ ∂_X(2 (a - 3)² ) = -3 ∂_X(X²) + 0 = -6x.

A na druhej strane na výpočet derivátu vzhľadom na a Je zabraný X ako konštanta:

∂_aF = ∂_a(-3x² + 2 (a - 3)² ) = ∂_a(-3x² )+ ∂_a(2 (a - 3)² ) = 0 + 2,2 (y - 3) = 4y - 12.

Príklad 2

Určiť čiastočné deriváty druhého poriadku:  ∂_Xxf, ∂_Rizornýf, ∂_YxF a ∂_XyF Pre rovnakú funkciu F Príklad 1.

Postup

V tomto prípade, pretože prvý čiastočný derivát je už vypočítaný v X a a (Pozri príklad 1):

∂_XxF = ∂_X(∂_Xf) = ∂_X(-6x) = -6

∂_RizornýF = ∂_a(∂_af) = ∂_a(4y - 12) = 4

∂_YxF = ∂_a(∂_Xf) = ∂_a(-6x) = 0

∂_XyF = ∂_X(∂_af) = ∂_X(4y - 12) = 0

Je pozorované, že ∂_YxF = ∂_XyF, Teda splnenie Schwarzovej vety, od funkcie F a jeho čiastočné deriváty prvého okruhu sú všetky nepretržité funkcie v R².

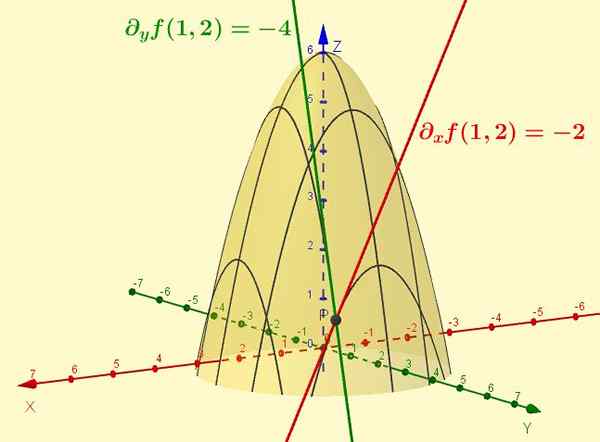
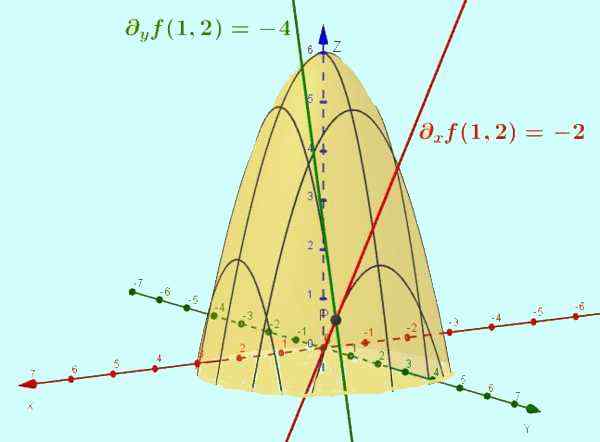Obrázok 2. Funkcia z = f (x, y) = -x2 - y2 + 6 je povrch znázornený na obrázku. Čiastočné deriváty vzhľadom na x je sklon tangenciálnej línie krivky, ktorý je výsledkom križovatky uvedeného povrchu s rovinou y = ctte (konkrétny prípad je zobrazený y = 2). Podobne časť F vzhľadom a je sklonom dotyčnice križovatky s x = 1, v bode (1, 2, 1).

Vyriešené cvičenia

Cvičenie 1

Byť funkciou:

Môže vám slúžiť: kvadratické úspechy: príklady, pravidlá a cvičenia vyriešené

f (x, y) = -x² - a² + 6

Nájdite funkcie G (x, y) = ∂_XF  a H (x, y) = ∂_aF.

Riešenie

Čiastočné deriváty F mať rešpekt z X, pre ktoré premenná a Stáva sa konštantným:

G (x, y) = - 2x

Podobne čiastočné deriváty g mať rešpekt z a, robí X konštantné, čo vedie k funkcii h:

H (x, y) = -2y

Cvičenie 2 

Vyhodnotiť bod (1, 2) funkcie f (x, y) a G (x, y) cvičenia 1. Interpretovať výsledky.

Riešenie

Hodnoty sa vymieňajú x = 1 a y = 2 Získanie:

f (1,2) = -(1)² -(2)² + 6 = -5 + 6 = 1

Toto je hodnota, ktorá pri hodnotení v tomto bode berie funkciu f.

Funkcia f (x, y) Je to dvojrozmerný povrch a koordinujte z = f (x, y) Je to výška funkcie pre každý pár (X, y). Keď je pár odobratý (1.2), Výška povrchu f (x, y) je Z = 1.

Funkcia G (x, y) = - 2x predstavuje rovinu v trojrozmernom priestore, ktorého rovnica je Z = -2x O dobre -2x + 0 a -z = 0.

Uvedené lietadlo je kolmo na lietadlo Xz A prejsť bodom (0, 0, 0). Pri hodnotení v x = 1 a y = 2 tak Z = -2. Všimnite si, že hodnota z = g (x, y) Je nezávislý od hodnoty priradenej premennej a.

Na druhej strane, ak sa povrch pretína f (x, y) S lietadlom y = c, s c konštantná, máte v lietadle krivku Zx: z = -x² - c² + 6.

V tomto prípade derivát z mať rešpekt z X sa zhoduje s čiastočným derivátom f (x, y) mať rešpekt z X: d_X Z = ∂_XF .

Pri hodnotení v páre (x = 1, y = 2) Čiastočné deriváty v tomto bode ∂_XF (1.2) Interpretuje sa ako sklon čiary dotyčku do krivky z = -x² + 2 bod (x = 1, y = 2) A hodnota tohto svahu je -2.

Odkazy

1. Ayres, f. 2000. Kalkulácia. 5ed. MC Graw Hill.
2. Čiastočné deriváty funkcie v niekoľkých premenných. Získané z: budovy.Uhorka.je.
3. Leithold, L. 1992. Výpočet analytickou geometriou. Harla, s.Do.
4. Purcell, e. J., Varberg, D., & Rigdon, s. A. (2007). Kalkulácia. Mexiko: Pearson Education.
5. Gorostizaga J. C. Čiastočné deriváty. Získané z: ehu.Eus
6. Wikipedia. Čiastočné deriváty. Obnovené z: je.Wikipedia.com.