Výpočet relatívnej hustoty, príklady, cvičenia

Ten Relatívna hustota Je to bezrozmerný vzťah medzi hustotou jednej látky a druhou referenčnou, ktorá je vo všeobecnosti voda pri 4 ° C (39.2 ° F) pre kvapaliny a tuhé látky, zatiaľ čo pre plyny sa používa suchý vzduch.

V niektorých textoch sa to tiež nazýva Špecifická hmotnosť (doslovný preklad z Špecifická hmotnosť v angličtine), ale je to rovnaký koncept. Obe hustoty musia byť v rovnakom systéme jednotiek a boli merané v rovnakých podmienkach tlaku a teploty.

Plávajúce objekty majú relatívnu hustotu menšiu ako hustota vody. Zdroj: Pixabay.

Relatívna hustota sa matematicky vypočíta takto:

Relatívna hustota = hustota vody/hustoty vody

Zatiaľ čo hustota akejkoľvek látky závisí od tlakových a teplotných podmienok, v ktorých sa meria, najmä pokiaľ ide o plyny, relatívna hustota je veľmi užitočnou koncepciou na rýchle charakterizáciu rôznych materiálov.

Ďalej sa to oceňuje, pretože hustota vody je približne 1 gram na kubický centimeter: 1 g /cm3 alebo 1 000 kg /m³, pri atmosférickom tlaku a v dobrom teplotnom rozmedzí (od 0 do 15 ° C).

Poskytnutím relatívnej hustoty látky je okamžite známe, ako svetlo alebo ťažké vzhľadom na vodu, univerzálna látka.

Okrem toho je relatívna hustota ľahko zapamätateľná, pretože sa meria s malými a ľahko manipulovateľnými číslami, ako bude vidieť v nasledujúcej časti, v ktorej sú hodnoty relatívnej hustoty uvedené pre niektoré známe látky.

[TOC]

Príklady

Relatívna hustota vody je očividne 1, pretože, ako je uvedené na začiatku, je to referenčný vzor pre kvapaliny a tuhé látky. Kvapaliny, ako je káva, mlieko alebo nealkoholické nápoje, majú relatívnu hustotu veľmi blízko k vode.

Pokiaľ ide o oleje, neexistuje žiadna jedinečná hodnota relatívnej hustoty použiteľnej pre všetkých, pretože závisí od jeho pôvodu, zloženia a spracovania. Väčšina relatívnej hustoty oleja je v rozsahu 0.7 a 0.95.

Môže vám slúžiť: Watt Law: Čo je, príklady, aplikácie

Plyny sú omnoho ľahšie, takže v mnohých aplikáciách je odobratý hustota vzduchu, takže relatívna hustota naznačuje, ako svetlo alebo ťažký plyn vzhľadom na vzduch. V porovnaní s vodou je relatívna hustota vzduchu 0.0013.

Pozrime sa na niektoré hodnoty relatívnej hustoty pre známe látky a materiály.

Relatívna hustota niektorých známych látok

- Ľudské telo: 1.07.

- Ortuť: 13.6.

- Glycerín: 1.26.

- Benzín: 0.68.

- Morská voda: 1.025.

- Oceľ: 7.8.

- Drevo: 0.5.

- Ľad: 0.92.

Hodnota relatívnej hustoty okamžite informuje, či látka alebo materiál pláva vo vode alebo naopak,.

Vzhľadom na to bude vrstva oleja na vrchole vody, pretože takmer všetky oleje majú relatívnu hustotu menšiu ako hĺbka tejto kvapaliny. Drevená kocka vo vode môže mať z nej rovnakým spôsobom ako ľad.

Rozdiel s absolútnou hustotou

Absolútna hustota je kvocient medzi hmotnosťou látky a objemom, ktorý zaberá. Pretože objem zase závisí od teploty (keď je dilatovaná väčšina látok) a tlaku, hustota zase závisí od týchto dvoch veľkostí. Matematicky máte:

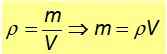
Kde ρ je hustota, ktorej jednotky v medzinárodnom systéme sú kg/m³, m je cesto a Vložka Je to objem.

V dôsledku vzťahu s objemom s teplotou a tlakom sú hodnoty absolútnej hustoty, ktoré sa objavujú v tabuľkách.

Môže vám slúžiť: Fyzická optika: História, časté podmienky, zákony, aplikácie

Tak, za normálnych podmienok pre plyny: 1 atmosféra tlaku a teplota 0 ° C, je hustota vzduchu stanovená v 1 v 1.293 kg/m³.

Aj keď jej hodnota prežíva tieto variácie, je veľmi vhodným množstvom na určenie správania látok, najmä v prostriedkoch považovaných za nepretržité.

Rozdiel s relatívnou hustotou spočíva v tom, že Absolute má rozmery, v takom prípade jej hodnoty závisia od systému vybraných jednotiek. Týmto spôsobom je hustota vody pri 4. C teploty:

ρ_{vodná voda} = 1 g /cm³ = 1 000 kg/m³ = 1.94 slimák/noha³

Vyriešené cvičenia

-Cvičenie 1

Nájdite objem obsadený 16 gramami oleja, ktorých relatívna hustota je 0.8.

Riešenie

Najprv nájdeme absolútnu hustotu ρ_olej olej. Označovanie ako s_g Jeho relatívna hustota je:

ρ_olej = 0.8 x hustota vody

Pre hustotu vody sa použije hodnota uvedená v predchádzajúcej časti. Ak je známa relatívna hustota, absolútna sa okamžite získa vynásobením tejto hodnoty hustotou vody. Tak:

Hustota materiálu = relatívna hustota x hustota vody (za normálnych podmienok).

Preto pre olej tohto príkladu:

ρ_olej = 0.8 x 1 g/cm³= 0.8 g/cm³

Pretože hustota je kvocient medzi hmotnosťou m a zväzok V, to zostane takto:

V = m/ρ = 16 g / 0.8 g/cm³= 20 cm³

-Cvičenie 2

Hornina má špecifickú hmotnosť 2.32 a objem 1.42 x 10 ^-4 m³. Nájdite váhu skaly v jednotkách medzinárodného systému a v technickom systéme.

Riešenie

Hodnota hustoty vody sa použije ako 1000 kg/m³:

Môže vám slúžiť: hnutie prekladu Zeme

ρ_húpací = 2.32 x 1000 kg/m³= 2.32 x 10³ Kg/m³

Masa m z skaly je v kilogramoch:

m = r_húpací . V = 2.32 x 10³ Kg/m³. 1.42 x 10 ^-4 m³ = 0.33 kg.

Hmotnosť jednotiek technického systému je 0.33 kilogramovej sily. Ak sa uprednostňuje v medzinárodnom systéme, potom je jednotka Newton, pre ktorú sa hmotnosť vynásobí hodnotou G, zrýchlenie gravitácie.

P = m. G = 0.33 kg. 9.8 m/s² = 3.23 n.

-Cvičenie 3

Piknomer je nádoba, s ktorou je možné určiť relatívnu hustotu látky pri určitej teplote.

Pycnometer. Zdroj: Wikipedia.orgán.

Na stanovenie hustoty neznámeho tekutiny v laboratóriu sa dodržiaval tento postup:

- Prázdny piknomer bol odvážený a čítanie bolo 26.038 g

- Potom piknomer s vodou pri 20 ° C (hustota vody 0.99823 g/cc) a vážené, získanie hodnoty 35.966 g.

- Nakoniec sa odvážil piknomer plný neznámeho kvapaliny a získané odčítanie bolo 37.791 g.

Žiada sa, aby odvodil výraz na výpočet hustoty kvapaliny a aplikoval ju s získanými údajmi.

Riešenie

Hmotnosť vody a tekutiny sa určuje odpočítaním čítania piknomeru plného prázdneho piknometra:

masa _H2o = 35.966 g - 26.038 g = 9.928 g; masa _plynulý  = 37.791 g - 26.038 g = 11.753 g

Nakoniec sa nahradí vo výraze, ktorý bol odvodený:

ρ_plynulý = (11.753 g / 9.928 g) . 0.99823 g/cc = 1.182 g/cc.

Odkazy

1. Britská encyklopédia. Špecifická hmotnosť. Získané z: Britannica.com.
2. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6^th… Ed Prentice Hall.
3. Mott, r.  2006. Tekutina. 4. Vydanie. Pearson Vzdelanie. 12-21.
4. Valera Negrete, J. 2005. Všeobecné fyzikálne poznámky. Žobrák. 44-45.
5. Biela, f. 2004. Tekutina. 5. vydanie. MC Graw Hill. 17-18.