História trigonometrie z jej pôvodu

Ten Trigonometria Vzťahuje sa na súbor faktov a pokrokov, ktoré sa vyskytli v tejto oblasti matematiky od jej pôvodu po najnovšie udalosti.

Pri krátkom výlete cez svoju históriu je zrejmé, že táto veda sa zrodila v reakcii na problémy, ktorým čelia starí astronómovia a navigátori, aby analyzovali vysídlenie hviezd na oblohe.

Tento termín sa objaví prvýkrát v knihe Trigonometriae Libri Quinque, ktorý napísal nemecký matematik a vedec Piticus Bartolomé (1561-1613). Cez Wikimedia Commons.

Podobne slovo trigonometria vyplýva zo zloženia dvoch gréckych slov: Trigonon (trojuholník) a Metron (rozsah). Tento výraz sa objaví prvýkrát v knihe Trigonometria -libri quinque, Napísal nemecký matematik a vedec Piticus Bartolomé (1561-1613).

Týmto spôsobom etymológia slova ukazuje, že trigonometria je štúdiom vzťahov medzi uhlami trojuholníka a segmentmi alebo čiarami, ktoré ho tvoria.

[TOC]

Začiatky trigonometrie

Prvé kroky trigonometrie vykonal človek, keď bol propagovaný potrebou poznať a analyzovať pohyb hviezd.

To znamená, že ľudská bytosť vymyslená trigonometria, pretože sa našla v situáciách, keď nebolo možné priamo robiť merania, pretože na výpočet hviezd boli potrebné zložitejšie matematické nástroje.

- Štúdie v Babylone

Bahenný stôl, ktorý napísali babylončania zvané Plimpton 322. Via: Wikimedia Commons

Štúdie ukazujú, že pred viac ako 3.000 rokov Babylončania už riešili koncept uhlov a trigonometrických dôvodov, to znamená, že boli schopní nadviazať vzťahy medzi stranami a uhlami trojuholníkov.

Napríklad bahenná tabuľka - napísaná babylončanmi - nazývaná Plimpton 322 (1800 a. C.) ukazuje postupnosť stĺpcov a riadkov, ktoré obsahujú čísla pri písaní Cuneiform. Podľa výskumu vykonaného niektorými odborníkmi tento tablet predstavuje to, čo sa javí ako séria trigonometrických funkcií.

Môže vám slúžiť: čo je usmernenie? (Geometria)

Babylončania boli oboznámení s pojmami, ktoré viedli k Pythagorasovej vete (569-474 a.C) a pochopili ich zásadu.

Rovnakým spôsobom tiež vedeli, že veta pripisovaná Thalesovi z Miletusu (695-546.C), čo naznačuje, že každý rovný, nakreslený rovnobežne so stranou trojuholníka, sa tvorí s ostatnými dvoma stranymi ďalší trojuholník, ktorý je podobný pôvodnému trojuholníku.

- Starí Egypťania

Starovekám Egypťanom sa podarilo udržiavať svah rovnomerne na každej pyramídnej tvári. Via: Pixabay

Aj keď nie je vhodné hovoriť o trigonometrii vo všeobecnej oblasti egyptskej matematiky, niet pochýb o tom, že táto civilizácia riešila určité trigonometrické koncepty.

Stáva sa to preto, že pri uvažovaní o veľkých budovách Egypťanov, ako sú pyramídy, možno dospieť k záveru, že mali určité vedomosti o trigonometrii.

Základné inžinierske ťažkosti, ktorým čelia Egypťania - a to vyriešilo úžasné.

Na tento účel použili koncept, ktorý nazývali „seqt“, a to je ekvivalentné tomu, čo dnes chápeme ako sklon nakloneného rovného povrchu.

Okrem toho Egypťania na meranie na zvislých povrchoch používaných ako jednotka „lakeť“ a v horizontálnej „ruky“, čo zodpovedalo 1/7 lakťa. Týmto spôsobom vypočítali sekt alebo čakajúce v rôznych budovách. Napríklad v pyramíde Jufú (Queope) je SEQT 5 1/2 ruky na lakeť.

- Staroveké Grécko a reťazcová tabuľka

Všetky znalosti Babylončanov a starovekých Egypťanov prešli do Grécka, kde sa zvýraznil matematik a astronóm Nicea (190-120 (190-120. C), ktorý sa považuje za otca trigonometrie. Hiparco vytvoril tabuľky „reťazcov“, s ktorými sa mu podarilo vyriešiť problémy s plochými trojuholníkmi.

Nicea Hiparco - Zdroj: Prevedené z.Wikipedia do Commons od Maksim - Podľa verejnej domény

Aby ich vytvorili, použil obvod s určitým polomerom (polomer je vzdialenosť medzi stredom kruhu a akýmkoľvek bodom obvodu).

Môže vám slúžiť: Podmienená pravdepodobnosť: vzorec a rovnice, vlastnosti, príklady

Potom vytlačil polomer, aby definoval rôzne uhly; Zatiaľ čo to bolo smerujúce do tabuľky.

Ukázalo sa, že tieto „reťazce“ sú prekurzormi tabuliek trigonometrických funkcií, ktoré dnes používame.

- Indické príspevky

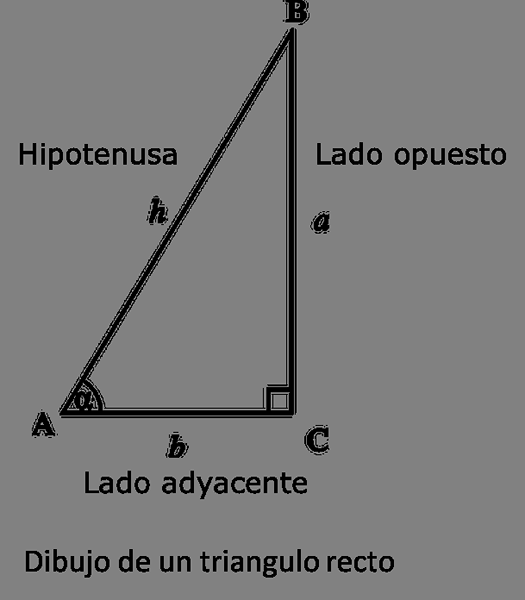Kreslenie pravého trojuholníka.

Rovnako ako v Grécku vedci, aj indickí astronómovia vyvinuli aj trigonometrický systém, ale na rozdiel od Grékov títo astronómovia založili svoju analýzu na funkcii „sine“ namiesto použitia reťazcov.

Funkcia „sine“ vyjadrená týmito astronómami však nie je dnes použitá; Táto funkcia nebola podiel (ako sa používa dnes), ale dĺžka opačnej strany ako uhol trojuholníka obdĺžnika, ktorého hypotenus je známa.

- Arábia a trigonometrické funkcie

Na konci ôsmeho storočia začali arabskí astronómovia ovplyvnení trigonometrickými štúdiami, ktoré uskutočnili národy Grécka a Indie, začali dôležité štúdie o vzťahoch medzi uhlami a ich stranami.

Týmto spôsobom na konci 10. storočia zdvihli dobre známe funkcie prsníka, kosínutia, dotyčničky, cotangent, sušiaci a harvest.

Objavili a overili primárne trigonometrické vety, ktoré sa používajú pri analýze plochých a sférických trojuholníkov. Arabskí matematici okrem toho navrhli použitie jednej hodnoty ("1") pre rádio (r = 1), čo viedlo k moderným hodnotám trigonometrických funkcií.

- Príspevky zo západu

Johann Müller známy ako Regiomontanus (1436-1476). Dosiahnutá systematizácia a zovšeobecnenie trigonometrických metód používaných v oblasti geometrie. Via: Wikimedia Commons

Matematika Západu, konkrétne medzi dvanásteho a pätnásteho storočia, bola silne ovplyvnená postulátmi starovekého Grécka, Indie a Arabov.

Môže vám slúžiť: Chi-kvadrát (χ²): Distribúcia, ako sa vypočíta, príklady

Počas tejto doby boli rozhodujúcimi v oblasti trigonometrie-príspevky Johanna Müllera, známeho tiež ako Regiomontanus (1436-1476). Tento matematik dosiahol systematizáciu a zovšeobecnenie trigonometrických metód používaných v oblasti geometrie.

Regiomontanus rozpracoval a uverejnil zmluvu, ktorú zavolal Z triangulis omnimodis libri quinque, ktorý bol zložený z piatich kníh a celkom 131 strán.

V tejto knihe reguloval všetky koncepty plochej a sférickej trigonometrie, ktoré následne používali dôležití astronómovia ako: Nicolás Copernic.

- Trigonometria sedemnásty a osemnásty storočia

Počas sedemnásteho storočia štúdie o trigonometrických výpočtoch prosperovali vďaka príspevkom matematikov, ako je Scotch John Napier (1550-1617), ktorý vzniesol rôzne metódy na riešenie sférických trojuholníkov.

John napier. Zdroj: Encard od Samuela Freemana (1773-1857) [verejná doména], cez Wikimedia Common

Neskôr, v 18. storočí, boli príspevky švajčiarskeho matematikového Leonharda Eulera (1707-1783) rozhodujúce, pretože jeho štúdie položili základy modernej trigonometrie zavedením zápisu, ktorý sa v súčasnosti používa na trigonometrické funkcie.

Okrem toho sa Eulerovi podarilo definovať exponenciálnu funkciu a objavil jeho vzťah s trigonometrickými funkciami, čo mu umožnilo opísať charakteristiky trigonometrie.

Následne Sir Isaac Newton (1643-1727) vymyslením diferenciálneho a integrálneho počtu uľahčoval reprezentáciu veľkého počtu matematických funkcií, medzi ktorými sú trigonometrické. Týmto spôsobom sa trigonometria stala súčasťou matematickej analýzy, kde dnes hrá základnú úlohu.

Ilustrácia sira Isaaca Newtona

Odkazy

1. Mansfield, Daniel. Wildberger, n. (2017). Plimpton 322 je babylonský presný sexuálny trigonometria. Získané 20. mája 2020 z: ScientDirect.com
2. Jimenez S. (2017). História trigonometrie a jej aplikácie. Získané 23. mája 2020 Deedu
3. Pérez, V. (2010). Trigonometria. Získané 22. mája 2020 z: LAGUIA2000.com
4. Siež.Do. (s.F.) Trigonometria. Získané 23. mája 2020 z: BlogSpot.com
5. Merlet, Jean-Pierre (2004). Poznámka o histórii trigonometrických funkcií. Získané 22. mája 2020 z: Net
6. Adamek, T., Penkalski, K., Valentín, G. (2005). História trigonometrie. Získané 23. mája 2020 z: Citseseerx.Ist.Psu.Edu/