Tuhé telo

Čo je to pevné telo?

Pevné telo je materiálny objekt, ktorého častice vždy zostávajú v rovnakých relatívnych polohách. Preto je to objekt, ktorý nie je deformovaný, kvalita pripísaná intenzívnym súdržným silám, ktoré udržiavajú častice na mieste.

Častice každého tela vystavené vonkajším silám majú tendenciu vibrovať alebo pohybovať, takže objekt sa do istej miery deformuje, ale tieto účinky sú zvyčajne malé.

Ak je to tak, možno predpokladať, že telo je tuhé a má veľmi dobrý prístup k svojmu správaniu, aj keď ide o idealizáciu.

Typy tuhých telies

Môžete rozlíšiť dva typy tuhého tela:

• Tí, ktorých častice prichádzajú v diskrétnych množstvách, to znamená, že môžu počítať. Napríklad dve kovové gule spojené tenkou a ľahkou tyčou sa môžu považovať za jedinečnú entitu. Ak je tyč dostatočne tuhá na to, aby sa neohýbala, systém sa považuje za tuhé telo.
• Tie, ktoré sú nepretržité, čo znamená, že častice, ktoré ich tvoria, sú nerozoznateľné. Objekty každodenné a prírodné sú dobré príklady: kamene, nábytok a ďalšie, ako aj pôda a iné nebeské skaly Rocky.

Pohyb a dynamika tuhého tela

Podobne ako objekty považované za častice, aj tuhé telá sa môžu prenášať, otáčať a majú všeobecnejší pohyb, kombinujúci preklad a rotáciu.

Preštudovanie prekladu nie je potrebné.

Tieto pohyby prekladov a rotácie môžu byť:

• Nezávislé, ako v prípade planét, ktoré majú pohyb rotácie okolo ich osi (považovaný za fixný) a ďalší preklad okolo slnka, ale rýchlosti každého z nich nesúvisia.
• Rozbité, ak súvisia s uhlovou rýchlosťou a rýchlosťou prekladu v strede hmoty. V tomto prípade je os rotácie mobilná, ako v prípade valca, ktorý klesá na streľbu bez skĺznutia sklonom sklonu.

Môže vám slúžiť: Prvý zákon termodynamiky: vzorce, rovnice, príklady

Dynamika rigidnej pevnej látky

V dynamike rigidnej tuhej látky sú relevantné nasledujúce veľkosti:

Hromadné centrum

Stred hmotnosti je bod, v ktorom sa celá hmotnosť tela považuje za koncentrovanú. Ak je to homogénne a symetrické telo, ako guľa, centrum hmoty sa zhoduje s geometrickým centrom.

Moment zotrvačnosti

Táto skalárna veľkosť je hodnota rotačnej zotrvačnosti alebo odporu, ktorá je proti objektu, aby sa otáčal okolo určitej osi. Závisí to úplne od geometrie objektu a jeho hmotnosti, a preto je v niektorých prípadoch ľahšie otočiť určité osi ako na ostatných.

Pre telá s dobre definovanými geometrickými tvarmi existujú tabuľky s momentmi zotrvačnosti vzhľadom na osi symetrie, napríklad ten, ktorý prechádza cez masový stred. S týmito informáciami a vetami súvisiacimi s momentom zotrvačnosti sa dajú ľahko vypočítať momenty vzhľadom na iné osi.

Sily a krútiaci moment alebo krútiaci moment

Sily sú povinné pohybovať sa telom. Ak sa tuhá pevná masová centrum presunie, pohybová rovnica, podľa druhého zákona Newtona, je:

F_Slepo = M ∙do_cm

Kde:

-Čistá sila je F_Slepo

-M je hmotnosť

-Zrýchlenie hmotnostného centra je do_cm

Nie všetky aplikované sily však prelomia objekt. Na tento účel je potrebný krútiaci moment alebo krútiaci moment, čo hovorí, ako efektívny je rotačný pôsobenie sily. Je definovaný ako vektorový produkt medzi vektorom polohy r Pokiaľ ide o určitý bod a silu F v otázke. Je označený gréckym listom τ (Tučným písmom, je to tiež vektor):

Môže vám slúžiť: eliptický pohyb

τ = r × F

V medzinárodnom systéme je jednotka krútiaceho momentu Nood (Newton na meter).

V mnohých prípadoch je rotačný pohyb okolo osi, ktorý prechádza stredom hmoty, opísaný analogickou rovnicou s druhým zákonom Newtona:

Kde indect „z“ sa vzťahuje na os rotácie, ktorá prechádza osou symetrie, pevného alebo pohybujúceho sa, ale bez zmeny smeru a_cm Je to okamih zotrvačnosti vzhľadom na stred hmotnosti a α_z Je to uhlové zrýchlenie tela. Leto pokrýva všetky vonkajšie momenty okolo osi Z.

Kinetická energia tuhej pevnej látky

Pohyb rigidného tela je opísaný prekladmi stredu hmotnosti a rotácií okolo tohto bodu, preto jej kinetická energia má obidva príspevky.

Nech k kinetická energia tela, v_cm Rýchlosť hmotnostného centra, hmotnosť tela a_cm jeho moment zotrvačnosti vzhľadom na stred hmotnosti a Ω uhlová rýchlosť. Dá sa preukázať, že kinetická energia je:

K = ½ mv_cm² + ½ i_cm Ω²

Zistilo sa, že druhým termínom vpravo je rotačný analóg zľava ľavej strany. Tam moment zotrvačnosti hrá rovnakú úlohu ako hmotnosť, zatiaľ čo uhlová rýchlosť má rovnakú úlohu ako lineárna rýchlosť.

Príklady v každodennom živote

Fyzické kyvadlo

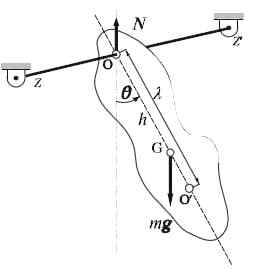Fyzické kyvadlo

Fyzické kyvadlo alebo skutočné kyvadlo sa dá veľmi ľahko zostaviť: pozostáva z tuhej pevnej látky ako tyč alebo tyč, voľne osciluje okolo horizontálnej osi. Os rotácie neprechádza stredom hmotnosti objektu a to v zásade môže mať akýkoľvek tvar.

Môže vám slúžiť: Odpor teplomer: Charakteristiky, prevádzka, použitie

Toto kyvadlo sa líši od jednoduchého kyvadla, pretože v druhom prípade sa uvádza, že hmotnosť, ktorá ju skladá, je presná.

Bicykel

Bicykel

Ďalším dobre známym príkladom tuhého tela je koleso bicyklov, ktorého os prechádza stredom hmoty, ktorá prechádza stredom kolesa. Pokiaľ sa nekúpia na bok alebo sa neotávajú, rovnice opísanej dynamiky sa vzťahujú na opis vášho pohybu.

Bowlingová lopta

Dobrým príkladom tuhého tela je bowlingová guľa

Rigidný tuhý model sa veľmi dobre prispôsobuje, aby opísal pohyb bowlingovej gule na trati alebo keď sa valí bez toho, aby sa skĺzol po spiatočnej rampe.

Yoyo

Yoyo je populárna hračka, ktorú je možné modelovať ako tuhé telo

Táto populárna hračka je vyrobená z dreva alebo plastového valca a lano ohromené v slote, ktorý ju obklopuje.

Valec možno modelovať ako tuhé telo, v ktorom napätie v šnúre poskytuje krútiaci moment na rotáciu, zatiaľ čo hmotnosť (aplikovaná na stred hmotnosti) a napätie je zodpovedné za vertikálne zrýchlenie stredu hmotnosti.

Odkazy

1. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill. 
2. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6. Ed Prentice Hall.
3.  Katz, D. 2013. Fyzika pre vedcov a inžinierov. Základy a spojenia. Učenie sa.
4. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 1. Pearson.
5. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 1. 7. Edimatizovať. Učenie sa.