Kvadrilaterálne prvky, vlastnosti, klasifikácia, príklady

A kvadrilaterálny Je to štvorprúdový polygón a štyri vrcholy. Ich opačné strany Sú to tí, ktorí nemajú spoločné vrcholy, zatiaľ čo sú po sebe idúce strany Tí, ktorí majú spoločný vrchol.

V kvadrilaterálnom sú susedné uhly Tí, ktorí zdieľajú stranu, zatiaľ opačné uhly Nemajú spoločné strany. Ďalšou dôležitou charakteristikou štvornásobného je to, že súčet jej štyroch Vnútorné uhly Je to dvojnásobok plochého uhla, ktorý je 360 ​​° alebo 2π radiánov.

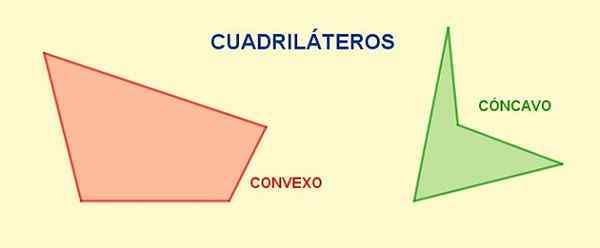
postava 1. Rôzne kvadrilaterály. Zdroj: f. Zapata.

Diagonály Sú to segmenty, ktoré spájajú vrchol s jeho opakom a v danom krúžku, z každého vrcholu môžete nakresliť jednu diagonálnu. Celkový počet diagonálov kvadrilaterálneho je dva.

Kvadrilaterály sú postavy známe ľudstvu od staroveku. Archeologické záznamy, ako aj stavby, ktoré dnes prežijú, svedčia o tom.

Aj dnes majú kvadriterály naďalej dôležitú prítomnosť v každodennom živote všetkých. Čitateľ môže nájsť tento formulár na obrazovke, na ktorej text číta v tomto presnom okamihu, v oknách, dvere, automobilové diely a nespočetné miesta viac.

[TOC]

Klasifikácia kvadrilaterálov

Podľa paralelizmu opačných strán sú štvornásobné klasifikované takto:

1. Lichobežník, Ak nie je paralelizmus a štvorkoliek je konvexný.
2. Lichobežník, Keď existuje paralelizmus medzi jediným párom opačných strán.
3. Rovnobežník, Keď sú ich opačné strany rovnobežné dve s dvoma.

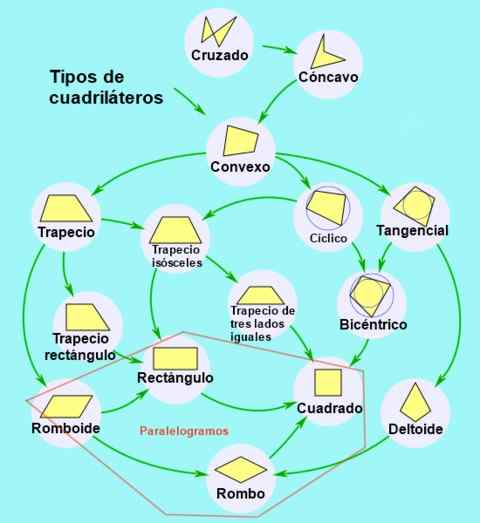Obrázok 2. Klasifikácia a subklasifikácia kvadrilaterálov. Zdroj: Wikimedia Commons.

Typy rovnobežníka

Na druhej strane je možné rovnobežníky klasifikovať podľa svojich uhlov a strán takto:

1. Obdĺžnik, Je to rovnobežník, ktorý má štyri vnútorné uhly rovnakej miery. Vnútorné uhly obdĺžnika tvoria pravý uhol (90 °).
2. Námestie, Je to obdĺžnik so štyrmi stranami rovnakej miery.
3. diamant, Je to rovnobežník so svojimi štyrmi stranami, ale jeho odlišné susedné uhly.
4. Naháňačka, rovnobežník s rôznymi susednými uhlami.

Lichobežník

Trapeze je konvexný štvoruholník s dvoma paralelnými stranami.

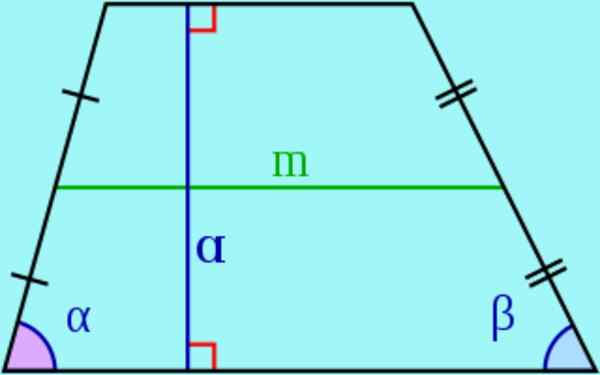Obrázok 3. Základne, bočné, výška a medián lichobežníka. Zdroj: Wikimedia Commons.

- V lichobeze sa nazývajú paralelné strany základne A nemagély sa nazývajú bočný.

- Ten výška z lichobežníka je vzdialenosť medzi dvoma základňami, to znamená dĺžka segmentu s koncami v základoch a kolmo na rovnaké. Tento segment sa tiež nazýva výška lichobežníka.

- Ten stredný Je to segment, ktorý sa spája so stredmi strán. Dá sa preukázať, že medián je rovnobežný so základňami lichobežníka a jeho dĺžka sa rovná semifotorizám základní.

- Oblasť lichobežníka je jeho výška vynásobená semi -bódiami základní:

Plocha lichobežníka = výška * (základňa 1 + základňa 2) / 2

Typy lichobežníka

-Obdĺžnik: Je to ten, ktorý má stranu kolmo na základne. Táto strana je tiež výškou lichobežníka.

-Lichobežné izoscely: Ten s rovnakou dĺžkou strany. V iSosceles lichobezoid sú uhly susediace so základňami rovnaké.

-Escaleno Trapezio: Ten, kto má svoje strany inej dĺžky. Jeho opačné uhly môžu byť akútne a druhé tupé, ale môže sa tiež stať, že obidve sú tupé alebo obidve akútne.

Môže vám slúžiť: Vyriešené faktorizačné cvičenia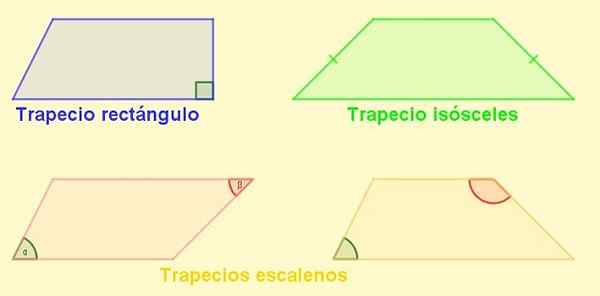 Obrázok 4. Typy lichobežníka. Zdroj: f. Zapata.

Rovnobežník

Rovnobežník je štvoruholník, ktorého opačné strany sú rovnobežné dve s dvoma. V rovnobežníku sú opačné uhly rovnaké a susedné uhly sú doplnkové alebo inými slovami, susedné uhly celkom 180 °.

Ak má rovnobežník pravý uhol, potom budú aj všetky ostatné uhly a výsledná postava sa volá obdĺžnik. Ale ak obdĺžnik má tiež susedné strany rovnakej dĺžky, potom sú všetky jeho strany rovnaké a výsledná postava je námestie.

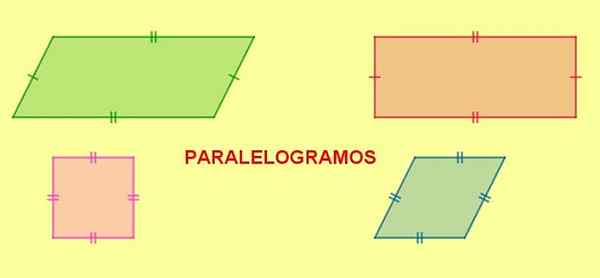Obrázok 5. Rovnobežník. Obdĺžnik, štvorec a kosoštvorca sú rovnobežníky. Zdroj: f. Zapata.

Ak má rovnobežník dve susedné strany rovnakej dĺžky, všetky jeho strany budú mať rovnakú dĺžku a výsledná postava je diamant.

Výška rovnobežníka je segment s koncami na opačných stranách a je na nich kolmé.

Plocha rovnobežníka

Plocha rovnobežníka je produktom základne podľa jej výšky, pričom základňa je bočnou kolmou do výšky (obrázok 6).

Plocha rovnobežníka = báza x výška = a . h

Diagonála rovnobežníka

Štvorec diagonálu, ktorý začína od vrcholu, sa rovná súčtu štvorcov oboch strán susediacich s uvedeným vrcholom viac dvojitým produktom týchto strán pri kosínusu uhla tohto vrcholu:

F² = a² +  d² + 2 a d cos (a)

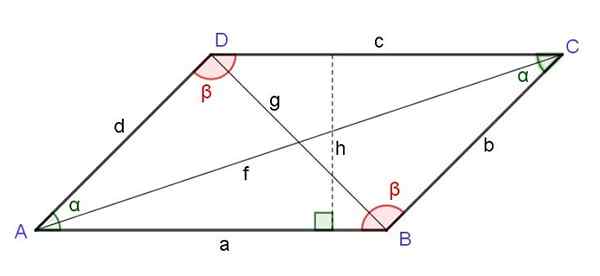Obrázok 6. Rovnobežník. OPPONE UHLES, výška, diagonály. Zdroj: f. Zapata.

Štvorec diagonálu na rozdiel od vrcholu rovnobežníka sa rovná súčtu štvorcov oboch strán susediacich s uvedeným vrcholom a odpočítal dvojitý produkt týchto strán kosínus uhlom tohto vrcholu:

g² = a² + d² - 2 a d cos (a)

Zákon o rovnobežníkoch

V akomkoľvek rovnobežníku sa súčet štvorcov ich bokov rovná súčtu štvorcov diagonálov:

do² + b² + c² + d² = f² + g²

Rekreactigle

Obdĺžnik je štvoruholník so svojimi opačnými stranami rovnobežnými dvoma dvoma a ktorý má tiež pravý uhol. To znamená, že obdĺžnik je typ rovnobežníka s pravým uhlom. Za rovnobežník, Obdĺžnik má svoje opačné strany rovnakej dĺžky a = c a b = d. 

Ale ako v akomkoľvek rovnobežní susedných uhloch sú doplnkové a rovnaké opačné uhly v obdĺžniku tým, že bude mať pravý uhol, bude nevyhnutne tvoriť priame uhly v ostatných troch uhloch. To znamená V obdĺžniku všetky vnútorné uhly merajú 90 ° alebo π/2 radiány.

Diagonála obdĺžnika

V obdĺžniku sú diagonály rovnaké, Ako bude uvedené nižšie. Dôvodom je nasledujúce; Obdĺžnik je rovnobežník so všetkými jeho priamymi uhlami, a preto zdedí všetky vlastnosti rovnobežníka vrátane vzorca, ktorý dáva dĺžku diagonálov:

F² = a²+  d² + 2 a d cos (a)

g² = a² + d² - 2 a d cos (a)

s α = 90 °

Ako Cos (90 °) = 0, Tak sa stáva, že:

F² = g² = a² +  d²

To je f = g, a preto dĺžky F a g Z dvoch diagonálov obdĺžnika sú rovnaké a ich dĺžka je daná:

Diagonálna dĺžka obdĺžnika = √ (a² + b²)

Okrem toho, ak je v obdĺžniku susedných strán do a b Jedna strana je založená na druhej strane bude výška, a preto bude oblasť obdĺžnika:

Môže vám slúžiť: Fibonacci Series: Vlastnosti, prírodné vzťahy, aplikácie

Obdĺžnik = a x b.

Obvod je súčet všetkých strán obdĺžnika, ale keďže sú protiklady rovnaké, potom je potrebný pre obdĺžnikový obdĺžnik do a b Obvod je daný nasledujúcim vzorcom:

Obvodový obvod = 2 (a + b)

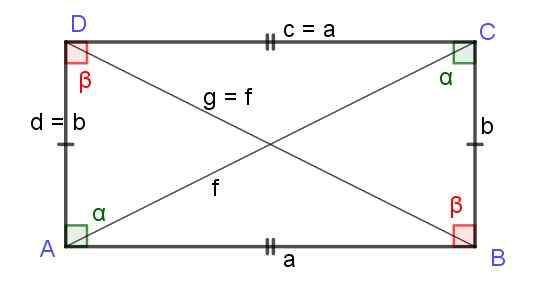Obrázok 7. Obdĺžnik strán A a B. Diagonály f a g majú rovnakú dĺžku. Zdroj: f. Zapata.

Námestie

Štvorec je obdĺžnik so susednými stranami rovnakej dĺžky. Ak má štvorec strana do, Potom jeho diagonály F a g Majú rovnakú dĺžku, čo je F = g = (√2) a.

Oblasť štvorca je jej strana zvýšená na štvorec:

Oblasť štvorca = a²

Obvod štvorca je dvojnásobok strany:

Obvod štvorca = 4 a

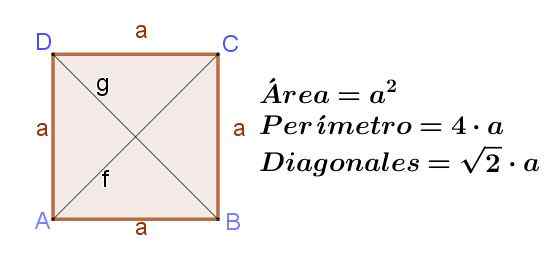Obrázok 8. Štvorcový od strany A, čo naznačuje jeho plochu, obvod a dĺžka jeho diagonálov. Zdroj: f. Zapata ..

diamant

Rhombus je rovnobežník so susednými stranami rovnakej dĺžky, ale rovnako ako v rovnobežníku sú opačné strany rovnaké, Všetky strany kostra sú rovnaké.

Diagonály kostra majú inú dĺžku, ale sú rezané v pravom uhle.

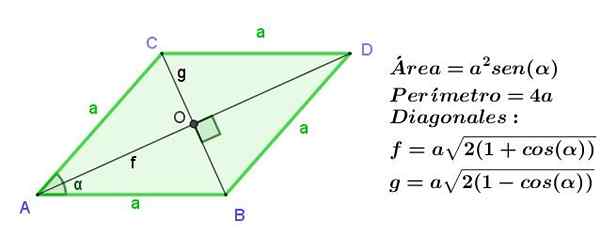Obrázok 9. Rhombus zo strany A, čo naznačuje jeho plochu, obvod a dĺžku jej uhlopriečok. Zdroj: f. Zapata.

Príklady

Príklad 1

Ukážte, že v kvadrilaterálnom (neprekročenom) vnútorných uhloch celkom 360 °.

Obrázok 10: Je demonštrované ako súčet uhlov štvornásobného pridania 360 °. Zdroj: f. Zapata.

ABCD sa považuje za ABCD (pozri obrázok 10) a nakreslený diagonálny BD. Vytvárajú sa dva trojuholníky ABD a BCD. Súčet vnútorných uhlov trojuholníka ABD je:

a + β₁ + Δ₁ = 180 °

A súčet vnútorných uhlov trojuholníka BCD je:

 p2 + γ + δ₂ = 180 °

Získa sa tieto dve rovnice:

a + β₁ + Δ₁ +  p₂ + γ + δ₂ = 180 ° + 180 °

Zoskupenie:

a + (p₁ +  p₂) + (δ₁ + Δ₂) + γ = 2* 180 °

Zoskupenie a prehodnocovanie sa konečne demonštruje, že:

a + β + δ + γ = 360 °

Príklad 2

Demonštrovať, že medián lichobežníka je rovnobežný so svojimi základňami a jeho dĺžka je semi -seismom základní.

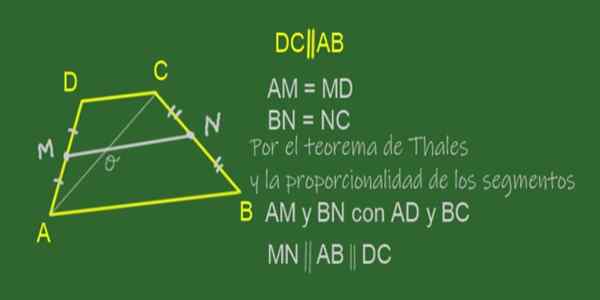Obrázok 11. Medián MN ABCD Trapeze. Zdroj: f. Zapata.

Medián lichobežníka je segment, ktorý sa spája s strednými bodmi jeho strán, to znamená, že nie sú paralelné strany. V lichote ABCD znázornenom na obrázku 11 je medián MN. 

Pretože je to stred AD a n Mid BC bod, je splnené, že kvocienty AM / AD a BN / BC sú rovnaké.

To znamená, že AM je úmerná BN v rovnakom pomere ako AD je BC, takže podmienky pre uplatňovanie vety (recipročnej) Thalesovej, ktoré potvrdzujú toto:

„Ak je v troch alebo viacerých priamých rezoch dvoma secant„.

V našom prípade sa dospelo k záveru, že línie MN, AB a DC sú navzájom rovnobežné, preto:

"LV mediáne je jeden z lichobežiek rovnobežný so svojimi základňami„.

Môže vám slúžiť: kombinované operácie

Teraz sa bude uplatňovať Thalesova veta:

„Sada paralelov znížených o dva alebo viac sušenia určuje proporčné segmenty„.

V našom prípade AD = 2:00, AC = 2 AO, takže trojuholník DAC je podobný trojuholníkovi Mao a následne DC = 2 mesiac.

Podobný argument umožňuje potvrdiť, že CU je podobný ako CON, kde CA = 2 CO a CB = 2 CN. Z toho vyplýva, že ab = 2 zapnuté.

Stručne povedané, ab = 2 na y 2 Mo. Takže keď sme odišli:

Ab + dc = 2 on + 2 Mo = 2 (mo + on) = 2 Mn

Nakoniec vymaže Mn:

Mn = (ab + dc) /2

A dospelo sa k záveru, že medián lichobežníka meria semi -bódiá základne alebo inými slovami: Medián meria súčet základov, rozdelený dvoma.

Príklad 3

Demonštrujte, že v kostore sú diagonály rezané v pravom uhle.

Obrázok 12. Rhombus a demonštrácia, že ich uhlopriečky sú rezané v pravom uhle. Zdroj: f. Zapata.

Rada na obrázku 12 ukazuje potrebnú konštrukciu. Najprv je ABCD rovnobežník nakreslený s AB = BC, to je rhombus. AC a DB Diagonals určujú osem uhlov znázornených na obrázku.

Pomocou vety (a.Jo.p.), ktoré uvádza, že interné alternatívne uhly medzi paralelami rezané secantom určujú rovnaké uhly, môžeme stanoviť nasledujúce:

α₁ = γ₁, a2 = γ2, δ₁ = Β₁ a δ2 = β2. (*)

Na druhej strane, ako sú susedné strany kosoštvorca rovnakej dĺžky, určujú sa štyri izosceles trojuholníky:

DAB, BCD, CDA a ABC

Teraz sa vyvoláva veta trojuholníkov (Isosceles), že uvádza, že uhly susediace s základňou sú rovnaké, kde sa dospelo k záveru, že:

Δ₁ = β2, δ2 = β₁, a2 = γ₁ a α₁ = γ2 (**)

Ak sú vzťahy (*) a (**) kombinované, dosiahne sa ďalšia rovnosť uhlov:

α₁ = a2 = γ₁ = γ₁ Na jednej strane a β₁ = Β2 = δ₁ = δ2 pre druhú. 

Pamätajúc na vetu rovnakých trojuholníkov, ktoré potvrdzujú, že dva trojuholníky s rovnakou stranou medzi dvoma rovnakými uhlami sú rovnaké:

AOD = AOB a následne aj uhly ∡AOD = ∡AOB.

Potom ∡AOD + ∡AOB = 180 °, ale keďže oba uhly sú rovnaké, 2 ∡AOD = 180 °, čo naznačuje, že ∡AOD = 90 °.

To znamená, že geometricky demonštruje, že uhlopriečky kosoštvorca sú rezané v pravom uhle.

Cvičenia vyriešené

- Cvičenie 1

Preukázať, že v obdĺžnikovom lichobežníku sú uhly, ktoré nie sú EG, doplnkové.

Riešenie

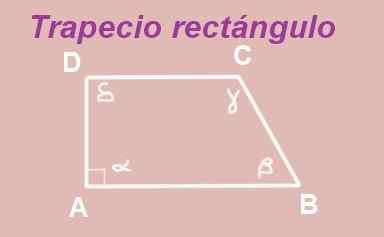Obrázok 13. Obdĺžnik. Zdroj: f. Zapata.

ABCD Lapezoid je postavený s paralelnými základňami AB a DC. Vnútorný uhol vrcholu A je rovný (meria 90 °), takže máte obdĺžnikový lichobežník.

Uhly a a δ sú vnútorné uhly medzi dvoma paralelnými paralelami AB a DC, preto sú rovnaké, to je δ = α = 90 °. 

Na druhej strane sa ukázalo, že súčet vnútorných uhlov štvoruholníka pridáva 360 °, to znamená:

a + β + y + δ = 90 ° + β + 90 ° + δ = 360 °.

Vyššie uvedené vedie k:

 β + δ = 180 °

Potvrdzujúc, čo chcelo preukázať, že uhly β a δ sú doplnkové.

- Cvičenie 2

ABCD rovnobežník má AB = 2 cm a ad = 1 cm, navyše uhol zlý je 30 °. Stanovte plochu uvedeného rovnobežníka a dĺžku jeho dvoch diagonálov.

Riešenie

Plocha rovnobežníka je produktom dĺžky jej základne podľa výšky. V tomto prípade sa dĺžka segmentu B = AB = 2 cm bude brať ako základ, druhá strana má dĺžku a = ad = 1 cm a výška H sa vypočíta takto:

H = ad * sin (30 °) = 1 cm * (1/2) = ½ cm.

Potom: oblasť = b * h = 2 cm * ½ cm = 1 cm².

Odkazy

1. C. A. Do. (2003). Elementy geometrie: s cvičeniami a geometria kompasu. University of Medellin.
2. Campos, f., Cerecedo, f. J. (2014). Matematika 2. Redakčná skupina Patria.
3. Oslobodený, k. (2007). Objavovať polygóny. Benchmark vzdelávacia spoločnosť.
4. Hendrik, v. (2013). Zovšeobecnené polygóny. Birkhäuser.
5. Iger. (s.F.). Matematika Tacaná. Iger.
6. Jr. Geometria. (2014). Polygóny. Lulu Press, Inc.
7. Miller, Heeren a Hornsby. (2006). Matematika: uvažovanie a aplikácie (desiate vydanie). Pearson Vzdelanie.
8. Patiño, m. (2006). Matematika 5. Redakčný progreso.
9. Wikipedia. Kvadrilaterály. Obnovené z: je.Wikipedia.com