Obdĺžnikové súradnice príklady a cvičenia vyriešené

Ten obdĺžnikové súradnice o Cartesian sú tie, ktoré sa získavajú pri premietaní ortogonálne na troch karteziánskych sekerách x, y, z bodu umiestneného v trojrozmernom priestore.

Karteziánske osi sú vzájomne kolmé orientované rovno. V karteziánskom súradnicovom systéme sú k každému bodu v priestore priradené tri skutočné čísla, ktoré sú jeho obdĺžnikovými súradnicami.

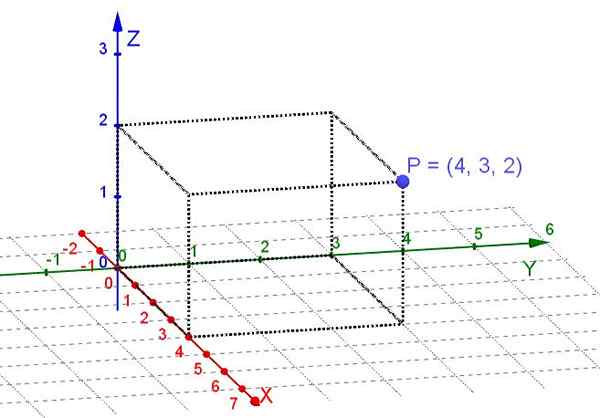
postava 1. Obdĺžnikové súradnice bodu P (vlastné rozpracovanie)

Lietadlo je podprostorom trojrozmerného priestoru. V prípade zvažovania bodov v rovine stačí zvoliť pár kolmých sekerov X a ako karteziánsky systém. Potom mu v každom bode lietadla sú priradené dve skutočné čísla, že jeho obdĺžnikové súradnice sú.

[TOC]

Pôvod obdĺžnikových súradníc

Obdĺžnikové súradnice pôvodne navrhli francúzsky matematik René Descartes (1596 a 1650), a preto dostávajú označenie karteziánov.

S touto myšlienkou Descartesu sú body roviny a priestoru priradené čísla, takže geometrické postavy spojené s algebraickou rovnicou a klasické geometrické vety sa môžu demonštrovať algebraicky. S karteziánskymi súradnicami sa zrodila analytická geometria.

Karteziánske lietadlo

Ak sa na rovine vyberú dve kolmé čiary, ktoré sa pretínajú v jednom bode alebo; a ak je každému riadku priradený smer a numerická stupnica medzi následnými rovnými bodmi, potom existuje karteziánsky systém alebo plán, v ktorom je každý bod roviny spojený s usporiadaným párom dvoch reálnych čísel, ktoré sú jeho projekciami na resp. x a y osi.

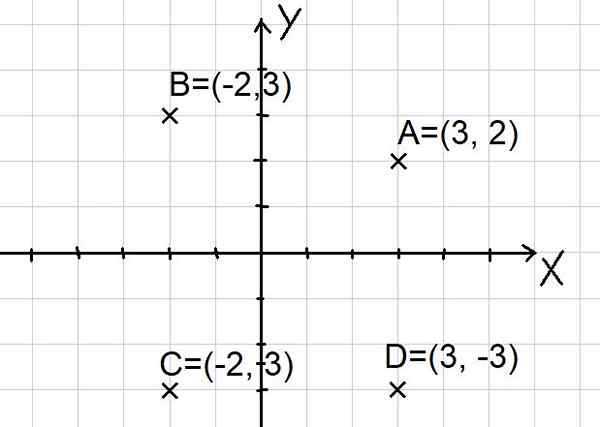
Body A = (3, 2); B = (-2, 3); C = (-2, -3) a D = (3, -3) sú znázornené v karteziánskej rovine, ako je uvedené nižšie:

Obrázok 2. Body na karteziánskom lietadle. (Vlastné rozpracovanie)

Všimnite si, že dve osi x a y rozdeľujú lietadlo na štyri sektory nazývané kvadranty. Bod A je v prvom kvadrante, B v druhom kvadrante, C v treťom kvadrante a bod D v štvrtom kvadrante.

Môže vám slúžiť: populácia a vzorka

Vzdialenosť medzi dvoma bodmi

Vzdialenosť medzi dvoma bodmi A a B karteziánskej roviny je dĺžka segmentu, ktorý ich spája. Túto vzdialenosť sa dá analyticky vypočítať nasledovne:

D (a, b) = √ (bx - ax)^2 + (od - ay)^2)

Predný vzorec sa získa aplikáciou vety Pythagory.

Použitie uvedeného vzorca na body A, B Obr. 2 je:

D (a, b) = √ (-2 - 3)^2 + (3 - 2)^2) = √ (-5)^2 + 1^2) = √ (26)

To znamená, že d (a, b) = 5,10 jednotiek. Všimnite si, že vzdialenosť bola získaná bez potreby merať s pravidlom, bol dodržaný úplne algebraický postup.

Analytická expresia čiary

Obdĺžnikové súradnice umožňujú analytické znázornenie základných geometrických objektov, ako je bod a čiara. Dva body A a B definujú jednu čiaru. Sklon čiary je definovaný ako kvocient medzi rozdielom v súradniciach a bodom B menej, vydelený rozdielom v súradniciach X bodu B menej A:

Čakanie = (od - ay)/(bx - ax)

Akýkoľvek bod súradníc (x, y), ktorý patrí do riadku (AB), musí mať rovnaký sklon:

Čakanie = (y - ay)/(x - ax)

Rovnica, ktorá sa získava rovnosťou svahov, je analytická alebo algebraická reprezentácia čiary, ktorá prechádza bodmi A a B:

(y - ay)/(x - ax) = (od - ay)/(bx - ax).

Ak vás berú za A a B, obdĺžnikové súradnice na obrázku 2 sú:

(Y - 2)/(x - 3) = (3 - 2)/( - 2 - 3)

(y - 2)/(x - 3) = -⅕

V tomto konkrétnom prípade existuje čiara s negatívnym sklonom -⅕, čo znamená, že umiestnená v bode čiary a zvyšovanie súradnice X v jednotke, súradnica a znižuje sa v 0,2 jednotkách. 

Môže vám slúžiť: Toroid alebo Toro Dona

Najbežnejším spôsobom, ako napísať rovnicu riadku v rovine, je súradnica a jasná ako funkcia premennej x:

y = -(1/5) x + 13/5 

Príklady

Príklad 1

Získajte analytickými metódami vzdialenosť medzi bodmi C a A, čo je obdĺžnikové súradnice C = (-2, -3) a úrovňami A = (3,2).

Vzorec euklidovskej vzdialenosti medzi týmito dvoma bodmi je napísaná takto:

D (a, c) = √ ((cx - ax)^2 + (cy - ay)^2)

Nahradenie jeho zodpovedajúcich obdĺžnikových súradníc, ktoré máte:

D (a, c) = √ (-2-3)^2 + (-3-2)^2) = √ (-5)^2 + (-5)^2) = 5√2 = 7,07

Príklad 2

Získajte rovnicu čiary, ktorá prechádza bodom C súradníc (-2, -3) a bodu súradnice (2, 0).

Po prvé, získa sa sklon čiary CP:

čaká = (0 -(-3)) / (2 -( -2)) = ¾ 

Akýkoľvek bod Q všeobecných obdĺžnikových súradníc (x, y), ktorý patrí do čiary CP, musí mať rovnaký sklon:

Čakanie = (y -(-3)) / (x -( -2)) = (y +3) / (x +2)

To znamená, že rovnica čiary CP je:

(Y +3) / (x +2) = ¾

Alternatívnym spôsobom, ako napísať rovnicu riadku CP, je vyčistenie a:

y = ¾ x - 3/2 

Vyriešené cvičenia

Cvičenie 1

Získajte obdĺžnikové súradnice priesečníka medzi čiarami y = - (1/5) x + 13/5 a čiara y = ¾ x - 3/2.

Riešenie: Podľa definície bod priesečníka týchto dvoch riadkov zdieľa rovnaké obdĺžnikové súradnice. Preto sú súradnice a v bode križovatky identické pre obidve riadky:

-(1/5) x + 13/5 = ¾ x - 3/2

Čo vedie k nasledujúcemu výrazu:

Môže vám slúžiť: obdĺžnik Trapezoid: Vlastnosti, vzťahy a vzorce, príklady

(¾ + ⅕) x = 13/5 +3/2

Získava sa riešenie súčtu frakcií:

19/20 x = 41/10

Vymazanie x:

x = 82/19 = 4,32

Na získanie hodnoty a priesečníka sa hodnota X získaná v jednom z riadkov vymení:

y = ¾ 4,32 - 3/2 = 1,74

To znamená, že dané čiary sú zachytené v bode I súradníc I = (4,32; 1,74).

Cvičenie 2

Získajte obvodovú rovnicu, ktorá prechádza cez obdĺžnikový súradnicový bod R (3, 4) a ktorá má centrum pri pôvode súradníc.

Riešenie: Rádio R je vzdialenosť od bodu R do pôvodu alebo súradníc (0, 0).

d (r, o) = √ ((rx - 0)^2 + (ry - 0)^2) = √ ((3 - 0)^2 + (4 - 0)^2) = √ (3^2 + 4^2) = √ (9 + 16) = √ (25) = 5

To znamená, že je to polomer 5 kruhu 5, ktorý je vycentrovaný na (0,0).

Akýkoľvek bod p (x, y) obvodu musí mať rovnakú vzdialenosť 5 do stredu (0, 0) pre to, čo je možné napísať:

D (p, o) = √ ((x - 0)^2 + (y - 0)^2) = √ (x^2 + y^2) = 5

To znamená:

√ (x^2 + y^2) = 5

Aby sa eliminovali druhý druhý koreň, obaja členovia rovnosti zostanú potichu:

x^2 + y^2 = 25

Aká je obvodová rovnica.

S týmto príkladom je ilustrovaný výkon obdĺžnikového súradnicového systému, ktorý umožňuje určiť geometrické objekty, ako napríklad obvod bez potreby používať papier, ceruzku a kompas. Bol stanovený obvod požadovaný iba algebraickými metódami.

Odkazy

1. Arfken G a Weber H. (2012). Matematické metódy pre fyzikov. Komplexný sprievodca. 7. vydanie. Akademická tlač. ISBN 978-0-12-384654-9
2. Výpočet. Obdĺžnikové súradnice vyriešené problémy. Obnovené z: výpočtu.Dc
3. Weisstein, Eric W. „Karteziánske súradnice.”Z Web Mathworld-A Wolfram. Obnovené z: Mathworld.Valfram.com
4. Wikipedia. Karteziánsky koordinačný systém. Zdroj: In.Wikipedia.com