Boltzmann Konštantná história, rovnice, výpočet, cvičenia

Ten Boltzmannova konštanta Je to hodnota, ktorá spája priemernú kinetickú energiu termodynamického systému alebo objekt s absolútnou teplotou rovnakej teploty. Aj keď sú často zmätení, teplota a energia nie sú rovnaké koncepty.

Teplota je miera energie, ale nie samotná energia. Pri konštante Boltzmann je jeden so sebou navzájom prepojený nasledovne:

A_c = (3/2) k_B  Tón

Boltzmann hostiteľ vo Viedni. Zdroj: Dadotet v angličtine Wikipedia [CC BY-SA 3.0 (http: // creativeCommons.Org/licencie/By-SA/3.0/]]

Táto rovnica platí pre ideálnu molekulu monookomického plynu m, kde A_c Je to jeho kinetická energia uvedená v joules, k_B Je to Boltzmannova konštanta a Tón Je to absolútna teplota v Kelvin.

Týmto spôsobom, keď sa teplota zvyšuje, sa zvyšuje aj priemerná kinetická energia molekulou látky, ako sa očakávalo. A opak sa stane, keď sa teplota zníži, keď je schopný dosiahnuť bod, v ktorom sa celý pohyb prestáva, dosiahne sa najnižšia možná alebo absolútna teplota.

Keď hovoríme o priemernej kinetickej energii, je potrebné si uvedomiť, že kinetická energia je spojená s pohybom. A častice sa môžu pohybovať mnohými spôsobmi, napríklad pohybujúce sa, rotujúce alebo vibračné. Samozrejme, nie všetci to urobia rovnakým spôsobom a keďže sú nespočetné, potom sa priemer chystá na charakterizáciu systému.

Niektoré energetické štáty sú pravdepodobnejšie ako iné. Tento koncept má radikálny význam v termodynamike. Energia zvažovaná v predchádzajúcej rovnici je kinetická energia prekladu. Pravdepodobnosť štátov a ich vzťah s Boltzmannovou konštantou bude hovoriť o niečo neskôr.

V roku 2018 bol Kelvin nanovo definovaný a s ním Boltzmann Constant, ktorá je v medzinárodnom systéme približne 1.380649 x 10^-23 J. Klimatizovať^-1. Oveľa presnosti je možné dosiahnuť pre Boltzmannovú konštantu, ktorá bola určená v mnohých laboratóriách po celom svete, rôznymi metódami.

[TOC]

História

Slávna konštanta dlhuje svoj názov fyzikovi Ludwigovi Boltzmannovi (1844-1906), narodeným vo Viedni, ktorý venoval svoj život ako vedca štúdiu štatistického správania systémov s mnohými časticami, z hľadiska newtonovskej mechaniky.

Aj keď je dnes existencia atómu všeobecne akceptovaná, v devätnástom storočí viera v to, či atóm skutočne existoval alebo bol umeleckým umelom, s ktorým bolo veľa fyzikálnych javov vysvetľovaných v úplnej diskusii.

Môže vám slúžiť: Normálny vektor: výpočet a príklad

Boltzmann bol silným obrancom existencie atómu a vo svojej dobe čelil tvrdej kritike svojej práce mnohých kolegov, ktorí sa domnievali, že obsahujú nerozpustné paradoxy.

Vyhlásil, že pozorovateľné javy na makroskopických hladinách možno vysvetliť prostredníctvom štatistických vlastností zložkových častíc, ako sú atómy a molekuly.

Táto kritika môže byť spôsobená hlbokou epizódou depresie, ktorá ho viedla k tomu, aby si vzal svoj vlastný život začiatkom septembra 1906, keď mal ešte veľa čo robiť, pretože bol považovaný za jedného z veľkých teoretických fyzikov svojej doby a tam bolo malé, že ďalší vedci prispejú k potvrdeniu pravdivosti ich teórií.

Nestalo sa to dlho po jeho smrti, keď by sa pridali nové objavy o povahe atómu a jeho volebných častíc, aby sa Boltzmann dal dôvod.

Boltzmannove konštantné a Planckove diela

Teraz, Boltzmannova konštanta klimatizovať_B Bol predstavený tak, ako je známe dnes po práci rakúskeho fyzika. Bol to Max Planck, vo svojom zákone o emisii čierneho tela, dielo, ktoré predložil v roku 1901, ktorý mu v tom čase dal hodnotu 1,34 x 10²³ J/k.

Do roku 1933 bol Boltzmann pridaný do Viedne ako platída plaku s definíciou entropie zahŕňajúcej slávnu konštantu: S = k_B protokol w, rovnica, o ktorej sa bude diskutovať neskôr.

Dnes je Boltzmannova konštanta nevyhnutná pri uplatňovaní termodynamických zákonov, štatistickej mechaniky a teórie informácií, z ktorých tento fyzik so smutným koncom bol priekopníkom.

Hodnota a rovnice

Plyny môžu byť opísané v makroskopických pojmoch a tiež v mikroskopických podmienkach. Pre prvý opis existujú koncepty, ako je hustota, teplota a tlak.

Malo by sa však pamätať na to, že plyn sa skladá z mnohých častíc, ktoré majú globálnu tendenciu k určitému správaniu. Je to ten trend, ktorý sa merala makroskopicky. Jedným zo spôsobov, ako určiť Boltzmannovu konštantu, je vďaka dobre známemu rovnici ideálnych plynov:

p.V = n. R. Tón

Tu p Je to tlak plynu, Vložka Je to jeho objem, n Je to počet prítomných mólov, R Je to konštanta plynov a Tón Je to teplota. V móle ideálneho plynu je splnený nasledujúci vzťah medzi produktom p.Vložka, a kinetická energia prekladu Klimatizovať Celá sada je:

Môže vám slúžiť: Korpuskulárny model hmoty

p.V = (2/3). Klimatizovať

Preto je kinetická energia:

K = (3/2) n.R.Tón

Rozdelením celkovým počtom prítomných molekúl, ktoré sa nazývajú N, sa získa priemerná kinetická energia jednej častice:

A_c = K /n

A_c= (3/2N) n.R.Tón

V mol je počet častíc n_Do, A preto je celkový počet častíc N = nnA, zostať:

A_c = (3/2nn_Do) n.R.Tón

Presne kvocient R/n_Do Je to Boltzmannova konštanta, ktorá sa demonštruje, že kinetická energia priemernej translácie častice závisí iba od absolútnej teploty a nie od iných veľkostí, ako je tlak, objem alebo dokonca typ molekuly:

A_c = (3/2) k_B. Tón

Boltzmannova konštanta a entropia

Plyn má danú teplotu, ale táto teplota môže zodpovedať rôznym vnútorným energetickým stavom. Ako vizualizovať tento rozdiel?

Zvážte súčasné spustenie 4 mincí a spôsoby, ako môžu spadnúť:

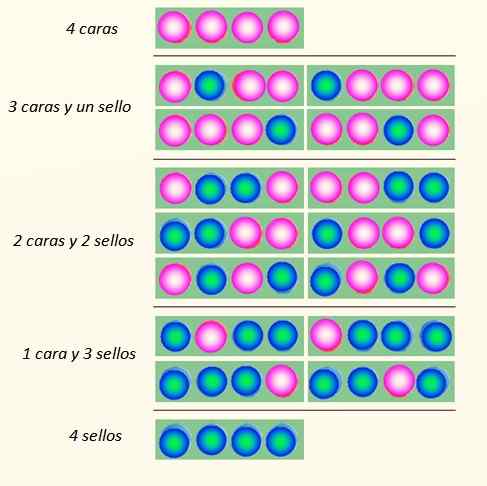Spôsoby, akými môžu 4 mince spadnúť. Zdroj: Self Made

Sada mincí môže predpokladať celkom 5 štátov, ktoré sa považujú za Makroskopický, opísané na obrázku. Ktorý z týchto štátov by čitateľ povedal, že je to najpravdepodobnejšie?

Odpoveď by mala byť stav 2 tvárí a 2 krížov, pretože má celkom 6 možností, zo 16 znázornených na obrázku. A 2⁴ = 16. Sú rovnocenné so štátmi mikroskopický.

A čo keď sa spustí 20 mincí namiesto 4? Celkom by bolo 2^dvadsať Možnosti alebo „mikroskopické stavy“. Je to omnoho väčšie a ťažšie číslo. Na uľahčenie riadenia veľkého počtu sú logaritmy veľmi vhodné.

Teraz je zrejmé, že štát s najväčšou poruchou je najpravdepodobnejší. Najviac usporiadané štáty, ako sú 4 tváre alebo 4 známky, sú o niečo menej pravdepodobné.

Entropia makroskopického stavu je definovaná ako:

S = k_B ln w

Kde W Je to počet možných mikroskopických stavov a klimatizovať_B Je to Boltzmannova konštanta. Ako ln w Je bezrozmerná, entropia má rovnaké jednotky ako k_B: Joule/k.

Toto je slávna rovnica v Boltzmannovom náhrobku vo Viedni. Viac ako entropia je však relevantnou zmenou:

Môže vám slúžiť: termodynamické premenné: ktoré sú a cvičenia vyriešené

Δs = k_B ln w₂ - klimatizovať_B ln w₁ = k_B LN (w₂/w₁)

Ako sa počíta K_B?

Hodnota Boltzmannovej konštanty sa získava experimentálne presne s meraniami založenými na akustická teplometria, ktoré sa vykonávajú pomocou vlastníctva, ktorá stanovuje závislosť od rýchlosti zvuku v plyne s rovnakou teplotou.

Rýchlosť zvuku v plyne je skutočne daná:

Kde b _adiabatický Je to modul adiabatickej kompresivity daný:

B_adiabatický = γp

A ρ je hustota plynu. Pre predchádzajúcu rovnicu, p Je to tlak príslušného plynu a γ Je to adiabatický koeficient, ktorého hodnota pre konkrétny plyn sa nachádza v tabuľkách.

Metrologické inštitúty zažívajú aj iné spôsoby merania konštanty, napríklad Johnson hluková teplometria, ktorý používa tepelné výkyvy, ktoré sa vyskytujú náhodne v materiáloch, najmä v vodičoch.

Vyriešené cvičenia

-Cvičenie 1

Nájsť:

a) Kinetická energia priemerného prekladu A_c ktorá má ideálnu molekulu plynu pri 25 ° C

b) Kinetická energia prekladu Klimatizovať molekúl v 1 mol tohto plynu

c) Priemerná rýchlosť molekuly kyslíka pri 25 ° C

Skutočnosť

m_kyslík = 16 x 10 ^-3 kg/mol

Riešenie

do) A_c = (3/2) k t = 1.5 x 1.380649 x 10^-23J. Klimatizovať^-1 x 298 K = 6.2 x 10^{-dvadsaťjeden} J

b) K = (3/2) n.R.T = 5 x 1 mol x 8.314 J/mol .K x 298 K = 3716 J

c) A_c = ½ MV², Berúc do úvahy, že molekula kyslíka je diatomická a molárna hmota sa musí vynásobiť 2, bude to:

-Cvičenie 2

Nájdite zmenu entropie, keď 1 mol plynu obsadených objemom 0.5 m³ Rozširuje sa na obsadenie 1 m³.

Riešenie

Δs = k_B LN (w₂/w₁)

W₂= 2^NW₁ (Boli 2⁴ Mikroskopické stavy na spustenie 4 mincí, nezabudnite?)

Kde n je počet častíc prítomných v 0.5 mol plynu 0.5 x n_Do:

Δs = k_B LN (2^N W₁/w₁) = k_B ln 2^N= k_B 0.5n_Do ln 2 = 2.88 j/k

Odkazy

1. Atkins, str. 1999. Fyzikálna chémia. Vydanie omega. 13-47.
2. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill. 664-672.
3. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6. ... Ed Prentice Hall. 443 -444.
4. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 1. 647-673.
5. Ak redefinícia. Kelvin: Boltzmann Constant. Získané z: NIST.Vláda