Ako získať percento? Príklady a cvičenia

Môcť získať percento S niekoľkými metódami. Môžete rýchlo vypočítať 10% ľubovoľného čísla iba pri pohybe desatinnej čiarky polohu doľava. Napríklad 10% zo 100 je 10; 10% z 1 000 je 100.

Ak chcete vypočítať zložitejšie percentá, ako napríklad 36% z 25 alebo 250% z 20, sú potrebné ďalšie metódy. V prípade, že systém 10% nie je použiteľný, je možné zohľadniť nasledujúce metodiky.

postava 1. Zľavy s rôznymi percentami. Koľko sa navzájom zachránime?. Zdroj: Pixabay.

Termálne percento znamená určitú časť každých stoviek a vzťahuje sa na aritmetickú operáciu, ktorá sa vykonáva na nájdenie uvedenej časti. Napríklad 20% („dvadsať percent“) sa číta v pesos, to znamená, že 20 pesos je zľavnených za každých 100 pesos.

Percento slúži na výpočet, ktorá časť celkového obsahu predstavuje sumu. V tomto prípade sa celková suma dostane na stupnicu 100 a percento informuje, koľko je na základe týchto 100 časťou, ktorá sa má vypočítať.

Pozrime sa, ako sa to robí s týmito príkladmi. V prvom rade to robíme vo forme zlomku:

• 20% = 20/100
• 5% = 5 /100
• 0,7% = 0,7 / 100
• 100% = 100 /100

Všimnite si, že 100% sa rovná 1. Percentá sa však dajú napísať aj desatinné:

• 20% = 0,20
• 5% = 0,05
• 0,7% = 0,007
• 100% = 1,0

Keď je vyjadrené percento určitého čísla, jednoducho Čiarka sa pohybuje Z toho číslo dva miesta vľavo. V percentuálnom podiele pravidlo proporcionality:

20% je 20 zo 100, preto:

20% zo 100 je 20, 20% z 200 je 40, 20% z 300 je 60, 20% z 50 je 10.

Všeobecné pravidlo pre 20 % akejkoľvek sumy

20% x je x *(20/16) = x *0,2 = 0,2 *x

Toto pravidlo sa môže ľahko rozšíriť na nájdenie akéhokoľvek iného percenta, ktoré je požadované. Pozrime sa, ako v nasledujúcej časti.

Cvičenie vyriešené s vzorcom na výpočet n% 

Vzorec, ktorý sa má čo najskôr zhrnúť a rýchlo vypočítať akékoľvek percento n je:

n % =(A * n)/100

Napríklad chcete vypočítať 25% zo 400

Potom n = 25 a a = 400, čo vedie k (400*25)/100 = 100

Príklad

Aké percento 60 je 24?

Riešenie

Vyžaduje sa to, čo je rovnocenné s otázkou, čo je N% zo 60, ktoré dáva 24?

Navrhujeme všeobecný vzorec:

60 * N / 100 = 24

Vyčistíme n S týmto postupom:

-100, ktorý sa delí na člena IZiédo Rovnosti, choďte k členovi správny násobenie. 

-A 60, ktoré sa vynásobia u člena vľavo Choďte k členovi správny delenie.

N = 24 *100 /60 = 2400/60 = 240/6 = 6 *40 /6 = 40

Dospelo sa k záveru, že 40% zo 60 je 24.

Vyriešené cvičenia na výpočet percentuálneho podielu 

Nižšie sú uvedené jednoduché cvičenia na začatie praktizovania vyššie uvedených.

Môže vám slúžiť: 15 najobľúbenejších legiend a mýtov

Cvičenie 1

Nájdite 50% z 90.

Riešenie

Tu x = 90, n = 50 % a vymeňte:

90 * 50% = 90 * (50 /100) = 4500 /100 = 45 

Je to celkom jednoduché, pretože 50 % akejkoľvek sumy je polovica tejto sumy a polovica 90 je 45.

Cvičenie 2

Nájdite 30% z 90.

Riešenie

90 * 30% = 90 * (30 /100) = 2700 /100 = 27

Percentuálny nárast

V každodennom živote je časté počúvať niečo, napríklad zvýšenie výroby, zvýšenie platu alebo vzostup produktu. Je takmer vždy vyjadrená v percentuálnej podobe.

Napríklad určitý produkt stojí 300 EUR, ale utrpel zvýšenie o 30%. Pýtame sa sami seba: Aká je cena novej produktu?

Prvým je vypočítať časť, ktorá zodpovedá zvýšeniu. Pretože nárast je 30 častí 100, takže zvýšenie zvýšenia na základe pôvodnej ceny o 300 je trojnásobok 30 dielov, tj 3*30 = 90.

Produkt zvýšil 90 EUR, takže nová konečná cena bude to, čo bude stáť zvýšenie predtým:

Nová cena = stará cena + 90 € = 390 EUR

Môžeme si vytvoriť vzorec na výpočet percentuálneho zvýšenia. Používame písmená na symbolizáciu cien, ako je tento:

-F je konečná hodnota

-Jo je počiatočná hodnota a

-n je nárast nárastu.

S týmito názvami by sa konečná hodnota vypočítala takto:

f = i + (i* n / 100)

Ale ako Jo Opakuje sa oboma, možno to považovať za spoločný faktorNa získanie tohto iného výrazu, rovnako platné:

F = i * (1 + n / 100)

Overmeme s už vyriešeným prípadom, produktom, ktorý stojí 300 EUR a zvýšil 30%. Preto sa ubezpečujeme, že vzorec funguje dobre:

Konečná cena = f = 300 € * (1 + 30/100) = 300 € * (1 + 0,3) = 300 € * 1,3 = 390 €

Cvičenie 3

Zamestnanec zarobil 1500 EUR, ale bol povýšený a jeho plat dosiahol 20% nárast. Aký je váš nový plat?

Riešenie

Poďme aplikovať vzorec:

F = 1500 € * (1 + 20/100) = 1500 € * (1 + 0,2) = 1500 € * 1,2 = 1800 €

Nový plat zamestnanca je 1800 EUR.

Percento klesá

V prípade zníženia, vzorec pre výpočet konečnej hodnoty F určitej počiatočnej sumy Jo to utrpelo pokles v n% je:

F = i * (1 - N / 100)

Je potrebné poznamenať, že kladné znamenie (+) vzorca v predchádzajúcej časti bolo nahradené záporným znamením (-).

Obrázok 2. Percentuálne oznámenie zľavy. Zdroj: Pixabay

Cvičenie 4

Produkt označený 800 EUR, ale dostal 15% zľavu. Aká je nová cena produktu?

Riešenie 4

Konečná cena podľa vzorca je:

F = 800 € * (1 - 15/16) = 800 € * (1 - 0,15) = 800 € * (0,85) = 680 EUR

Konečná cena so zľavou 15% je 680 EUR, čo predstavuje úsporu 120 EUR.

POLEPŠIE PERCENTY

Objaví sa, keď určitá suma trpí percentuálnou variáciou a potom sa uplatňuje ďalšie percento. Napríklad produkt, ktorý mal dve percentuálne zľavy v rade. Ďalším príkladom je príklad zamestnanca, ktorý mal zvýšenie dvoch po sebe idúcich platov.

Môže vám slúžiť: Dôležitejšie ekonomické činnosti yucatánu

- Zvyšuje sa následné percento

Základňa roztoku v týchto prípadoch je rovnaká ako jedinečné zvýšenie, je však potrebné vziať do úvahy, že druhé zvýšenie percentuálneho podielu sa vykonáva pri konečnej hodnote prvého zvýšenia.

Predpokladajme, že produkt, ktorý vzrástol najskôr o 10% a potom 5%. Je nesprávne tvrdiť, že utrpel nárast o 15%, v skutočnosti to bolo viac ako toto percento.

Formuly pre konečnú hodnotu by sa uplatňovali takto:

-Prvá sa vypočíta konečná hodnota prvého zvýšenia o N1%

f1 = i + i * n1 / 100

-A potom, aby sa našla konečná hodnota druhého zvýšenia o N2%, konečná hodnota F1 sa považuje za počiatočnú hodnotu. Preto:

F2 = f1 + f1 * n2 /100 

Cvičenie 5

Kniha pôvodne stála 55 EUR, ale kvôli jej úspechu a vysokému dopytu utrpela dva po sebe idúce zvýšenie pôvodnej ceny. Prvý nárast bol 10% a druhý z 20%. Aká je konečná cena knihy?

Riešenie

-Prvé zvýšenie:

F1 = 55 € * (1 + 10 /100) = 55 € * 1,1 = 60,5 €

-Druhé zvýšenie

F2 = 60,5 € * (1 + 20/100) = 60,5 * 1,2 = 72,6 €

Konečná cena je 72,6 EUR.

Cvičenie 6

V súvislosti s predchádzajúcim cvičením. Tieto dve po sebe idúce zvýšenie: na aké percento jedinečného nárastu oproti pôvodnej knižnej cene zodpovedajú?

Riešenie

Ak zavoláme n% na percento jedinečného zvýšenia, vzorec, ktorý súvisí s týmto jedinečným percentom, sa zvýši na pôvodnú hodnotu a konečná hodnota je:

F2 = i *(1 + n / 100) 

To znamená:

72,6 € = 55 € + 55 € * (n / 100)

Vymazanie zvýšenia zvýšenia N% = (N /100), máme:

(N / 100) = (72,6 - 55 EUR) / 55 € = 17.6 /55 € = 0,32

Preto:

N = 0,32 * 100 = 32

Za cenu knihy sa použilo celkový percentuálny nárast o 32%. Všimnite si, že toto zvýšenie je väčšie ako súčet dvoch po sebe idúcich percentuálnych zvýšení.

- Postupné percentuálne zľavy

Myšlienka je podobná myšlienke, ktorá sa zvyšuje. Druhá percentuálna zľava sa musí vždy uplatniť na konečnú hodnotu prvej zľavy, pozrime sa na príklad:

Cvičenie 7

10% zľava, po ktorej nasleduje druhá zľava 20% na objekt, na ktorú je jedinečná percentuálna zľava rovnocenná?

Riešenie

-Prvá zľava:

F1 = i - i * n1 / 100  

-Druhá zľava

F2 = f1 - f1 * n2 / 100

Nahradenie prvej rovnice v druhej zostávajú:

f2 = (i - i * n1 / 100) - (i - i * n1 / 100) * n2 / 100

Rozvíjame tento výraz, dostaneme:

f2 = i - i* n1 / 100 - i* n2 / 100 + i* (n1 / 100) (n2 / 100) 

Kreslenie spoločného faktora Jo:

f2 = i * (1- N1% - N2% + N1% * n2%)

Nakoniec sa percentá uvedené v otázke vymenia:

F2 = i * (1 - 10% - 20% + 10% * 20%) = i * (1 - 0,1 - 0,2 + 0,1 * 0,2)

f2 = i * (1 - 0,3 + 0,02) = i * (0,72) = i * (1 - 0.28) = i * (1 - 100 /100) = i * (1 - 28%)

Inými slovami, následné zľavy 10% a 20% zodpovedajú jedinečnej 28% zľavy.

Pokročilé cvičenia

Skúsme tieto cvičenia iba vtedy, keď boli myšlienky predchádzajúcich dostatočne jasné.

Môže vám slúžiť: ľahké a krásne geografické obaly, obaly, obrázky

Cvičenie 8

Základ trojuholníka meria 10 cm a výška 6 cm. Ak sa dĺžka základne zníži o 10%. V akom percente by sa mala zvýšiť výška, aby sa oblasť trojuholníka nezmenila?

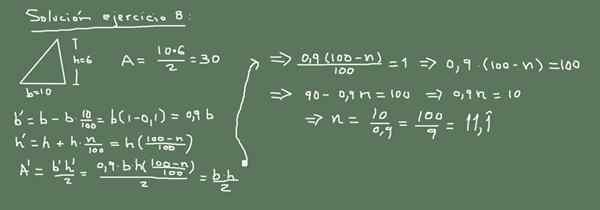Obrázok 3. Alternatívne riešenie cvičenia 8. Pripravený spoločnosťou F. Zapata.

Riešenie 8

Pôvodná oblasť trojuholníka je:

A = (10 cm * 6cm) / 2 = 30 cm²

Teraz, ak sa základňa zníži o 10%, potom jej nová hodnota je:

Nová základňa = 10 - (10/100) x 10 = 9 cm.

Nová hodnota výšky bude X a pôvodná oblasť sa musí udržiavať nezmenená, takže:

(9 cm * x) /2 = 30 cm²

Potom sa hodnota x vymaže ako:

X = 60 cm² / 9 cm = (20/3) cm = 6 666 cm

Čo znamená zvýšenie o 0,666 v porovnaní s pôvodnou hodnotou. Pozrime sa teraz, aké percento z toho predstavuje:

6 666 = 6 + (6 * N/100) 

6 666 -6 = 6 * n/100

0.666 = 6 * N/100

N/100 = 0,111

N = 11,1

Odpoveď znie: Výška sa musí zvýšiť o 11,1%, aby oblasť trojuholníka zostala rovnaká.

Cvičenie 9

Ak sa plat zvýši o 20%, ale potom daňové zľavy o 5%, aké je skutočné zvýšenie, ktoré pracovník prijíma?

Riešenie 

Najprv vypočítame zvýšenie N1%:

f1 = i + i * n1 / 100

Potom použijeme zľavu N2%:

F2 = f1 - f1 * n2 / 100

Prvá rovnica je nahradená v druhej:

f2 = i + i * n1 / 100 - (i + i * n1 / 100) * n2 / 100

Predchádzajúci výraz sa vyvíja:

f2 = i + i * n1 / 100 - i * n2 / 100 - i * (n1 / 100) * (n2 / 100)

Nakoniec je odstránený Jo Spoločný faktor a hodnoty N1 = 20 a N2 = 5, ktoré sa objavujú vo vyhlásení, sa nahradia:

F2 = i (1 + 0,2 - 0,05 - 0,2* 0,05) = i* (1 + 7/50) = i* (1 + 14/100) = i* (1 + 14%)

Pracovník dostal čistý nárast o 14%.

Cvičenie 10

Rozhodnite sa, čo je medzi týmito dvoma možnosťami najpohodlnejšie:

i) Získajte T -shirts so zľavou 32 %.

Ii) Kúpte si 3 t -shirty za cenu 2.

Riešenie 

Každú možnosť analyzujeme osobitne a potom vyberieme najkonomómnejšie:

i) Nech x je súčasná cena košele, zľava 32 % predstavuje konečnú cenu XF:

Xf = x - (32/100) x = x - 0.32x = 0.68x

Napríklad nákup 3 košieľ znamená výdavky 3 x 0.68 x = 2.04x

ii) Ak X je cena košeľa, za 3 košele jednoducho zaplatíte 2x.

Predpokladajme, že tričko má hodnotu 6 eur, so zľavou 32 % by to malo hodnotu 4.08 eur. Kúpte si 1 t -shirt nie je platná možnosť v ponuke 3 × 2. Takže ak si chcete kúpiť iba 1 tričko, zľava je výhodnejšia.

Ale ak je to, čo chcete kúpiť za desiatky, ponuka 3 × 2 je o niečo lacnejšia. Napríklad 6 T -shirts so zľavou by išlo za 24.48 eur, zatiaľ čo s ponukou 3 × 2 by stálo 24 eur

Odkazy

1. Ľahká trieda. Percentuálny podiel. Zdroj: Učebňa.com
2. Baldor a. 2006. Praktický teoretický aritmetický. Kultúrne vydania.
3. Educa Kids. Ako sa naučiť vypočítať percentá. Získané z: vzdelávacích.com
4. Gutiérrez, G. Finančné matematické poznámky. Získané z: CSH.IZT.Uam.mx
5. Inteligentné kliešte. Percento: Čo je a ako sa vypočíta. Získané z: Smartick.je